常用方法：建立满意度函数

姚新胜等（2004）总结了常见的几种满意度函数的建立方法。

（1）基于目标函数的直接法。在许多情况下，对解的满意程度是目标满意程度的一种直接体现，因此建立和目标函数有直接联系的满意度函数比较直观合理。特别是对于目标函数具有解析表达式、量化程度高的问题，满意度的建立就更加容易。

由目标函数导出满意度应该满足：

①在满意度函数中，各目标函数的作用应保持合理的数量级比例，以保证各目标具有合理的重要程度和变化趋势；

②解的满意程度的变化应在满意度函数中反映出来；

③对于每一个解必须存在和它对应的唯一满意度。

将目标函数转化为满意度函数，可以采用线形函数、指数函数或目标函数的某种组合等形式。

对于理想的最好解和最差解已知的情况，如果解空间和满意度有某种函数关系，可以采用类线性函数（线性函数的某种扩充形式）。线性满意度函数可表示为

对于复杂的目标函数情况，满意度可能是目标函数的某种组合形式，即

s=f(F1(x),F2(x),…,Fn(x))　(3.2)

式中，Fi（x）（其中i=1，2，…，n）是目标函数。

（2）按照解的搜索代价建立满意度函数。根据求解代价来衡量解的满意度，求解代价迅速增加的时刻可能是满意解基本找到的一种象征。

对于求解代价对问题较重要的一些情况，比如玉米地里寻找大玉米的问题，搜索过程本身具有一定的代价，如果搜索代价远远超过了解本身的价值，那么这个问题求解的意义就不大了。此时，建立与问题搜索过程的代价相关的满意度函数比较合理。

在建立过程中，满意度函数的自变量可能是搜索代价或搜索代价的某个函数形式，而满意度可以采取Huang（1979）介绍的某种形式。

对于整个解空间来讲，搜索代价函数为

式中，C（xi）为搜索xi所花费的代价；Cd（xi）为搜索xi已经花费的代价；Cw（xi）为搜索xi将要花费的而没有花费的代价。

在某个搜索时刻，对于解xi，Cd（xi）和Cw（xi）有且只能有一个，符合择一定理。

当采用某算法进行搜索时，如果对可能的搜索代价可以估计，则满意度可表示为

（3）利用模糊逻辑确定满意度函数。有些问题，其满意度函数不清晰，或者其目标函数或约束函数具有模糊性，那么建立模糊的满意度函数可能更适用，更能反映问题的本质。利用模糊逻辑建立满意度有两种方法。

①对于解和评价集都具有模糊性的情况，利用模糊关系的隶属度来表示其满意度。

通过建立目标评价集的一个模糊子集来实现从解到评判集再到满意集的一个映射，其中评判集元素的隶属度就是待求的满意度。

②在多数情况下，问题的解清晰存在，但是评判的标准是模糊的，此时可通过建立半模糊映射获取满意度。

设U∈F（X），∈F（Y），称Fuzzy关系为U到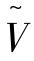的半Fuzzy映射，如果∀λ∈[0，1]，fλ是U到Vλ的映射。当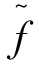是U到的半Fuzzy映射时，记为

(www.xing528.com)

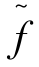如果∀λ∈[0，1]，fλ是U到的单射，称：U→为半Fuzzy单射；如果∀λ∈[0，1]此时（fλ（U）⊂Vλ），fλ是U到的满射，称：U→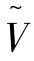为半Fuzzy满射；如果fλ既是半单射又是半满射，则称：U→为半Fuzzy双射。

为了方便，用表示的隶属函数，此外，由分解定理，有

式中

这里的就是我们要获取的解x的满意度。

（4）利用神经网络确定满意度函数。对于一些可能存在理想（或事实）最好解和最差解，或者存在部分解和满意度之间的关系问题，可通过BP神经网络映射功能来得到这种蕴涵关系。其实现思路是：首先对问题进行分析，收集并整理那些已经确认的可行解、非劣解，以及用户对这些解的评价，形成一个数据集，再以解向量及相关因素作为一个BP网络的输入，以对解的评价作为这个神经网络的输出，然后用数据集训练网络，反复进行这个过程，直到神经网络能模拟所有的输入、输出数据。一旦神经网络稳定，它的最终结构就可用来确定任一解的满意度。通过网络强大的映射功能，把解的满意度映射出来。

实际应用中，给出满意度函数的具体表达式却非常重要。一个合理的满意度函数应该满足如下的基本原则：

①真实性、正确性和合理性：满意度函数应能如实反映用户对解的评价体系要求；

②实用性：满意度函数要够用、要能用；

③简洁性：合理的满意度函数应该是在使用上尽量简单，适合于分析计算。

在各性能指标独立，且满意解d的最好解d1和最差解d2已知的情况下，解的独立满意度s的显式表达形式有线性、幂指数、双曲、分段线性函数等[383]，如图3.1所示。以下给出了常见连续型满意度函数的具体形式（以单调减函数为例）：

图3.1　解的独立满意度s的显式表达形式

①降半矩形函数，其表达式为

②降半Г函数，其表达式为

③降半正态函数，其表达式为

④降半柯西函数，其表达式为

⑤降半梯形函数，其表达式为

⑥降半岭形函数，其表达式为

非线性形式的满意度函数虽然能够更真实体现决策者设计意图，当偏好信息不明确时，通常难以实现。因此，如何利用相对较少偏好信息构造非线性形式的满意度函数成为影响模糊优化方法求解质量的关键。