交互式多目标优化方法在稳健设计中的实践应用

稳健设计要求产品系统性能对于制造过程中的波动或其工作环境的变化不敏感，而且尽管零部件会漂移或老化，系统仍然在其寿命期间可以持续工作。另一方面，工程稳健设计通常要求通过调整设计变量与控制其容差来使各种因素对产品质量的影响限制在规定的容许范围之内[145-151]，通常实际的工程优化设计的产品质量和成本控制过程中存在着大量信息不明确的影响因素，设计者往往很难在稳健设计初期就给出其精确的控制信息。因而，交互式模糊稳健设计方法（基于模糊物理规划模型的交互式优化设计）称为该领域研究热点。针对上述问题，陈守煜（1998）提出了模糊稳健设计准则，建立了模糊稳健设计的单目标优化模型。Dubois（1985）将容差和优质品率作为优化目标，建立了双目标优化模型。该方法以主容差作为优化目标，适用于各容差间难以确定其关系的情况。Klau（2002）从不确定因素引起产品质量波动的角度建立模糊稳健设计模型，但采用折衷规划求解时需面临权值的合理性选择问题。本书将在上述工作基础上，建立新的交互式多目标模糊优化稳健设计方法。

（1）改进的模糊稳健优化设计模型。广义地讲，产品质量优劣的评价是模糊的。因此，产品质量指标y可以定义为模糊指标，其隶属函数为为y的优质性的模糊概率描述。f（y）为y的分布密度函数，它同时受系统的可控因素和噪音因素的影响。产品设计方案的优劣或产品设计质量的品质稳健设计准则[373]可表示为

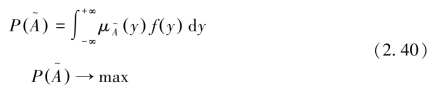
另一方面，设计参数的容差是衡量产品性能和制造成本的一个重要因素。容差愈小，虽可提高产品的质量和可装配性，但却大大提高了产品的制造费用。稳健设计中，在考虑产品品质的同时，还应该考虑到产品的可制造性，使产品的制造成本越低越好。采用主容差的最坏情况模型[374]建立的容差稳健设计准则可表示为

Berayoun等（1971）给出的稳健设计的双目标优化模型为

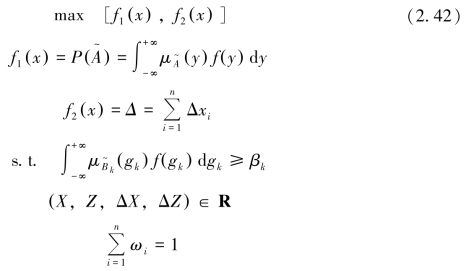
式中，βk为预定的稳健设计水平；为模糊约束条件所决定的安全事件，其定义为

其中，的隶属函数为的分布密度函数为fk（gk）。

该模型没有考虑各设计参数容差间相对关系，这意味着对各设计变量的稳健Pareto解集“缩放”程度的控制是置于同一标准下的。实际上，不同设计参数的容差对系统整体稳健特性的影响程度不同，即各容差具有不同重要性。因此，准则2仅适用于各设计变量容差间相对重要关系难以确定或可忽略情况。考虑各容差间的模糊相对重要程度时，上述模型可改写为

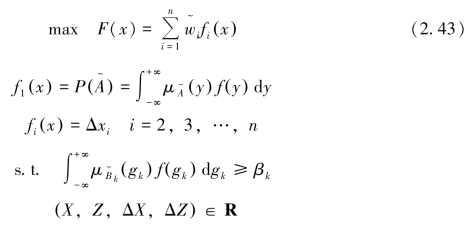
其中，权重系数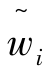表示各容差的模糊相对重要度。（2）基于FWPP的模糊稳健优化模型。当求解上述形式多目标模糊稳健优化问题的Pareto曲面满意区域的最佳调和解作为最终稳健设计方案时，可建立如图2.13所示的基于FWPP的模糊稳健优化模型（以FWPP模型为例）。

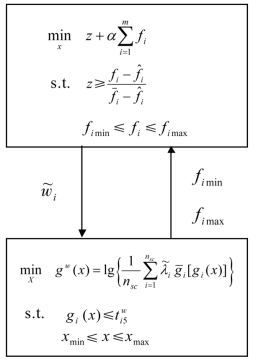
图2.13　基于FWPP的模糊稳健优化模型

该模型分为决策层和分析层。分析层求解得到满意稳健解集，提供给决策层评价；决策层根据评价结果将对候选解集的满意程度反馈给分析层，从而改进分析层的局部偏好，继续分析。该过程反复进行直至决策者满意为止。

（3）应用实例：风电增速箱轴承游隙的稳健设计。风力发电机组（风电机组）要求高可靠性，这是因为一旦发生故障，不仅会使运转率降低、发电量减小，而且维修、更换零件等需要的费用高昂。由于风电机组工作环境的特殊性和载荷的复杂性，大部分故障集中在增速箱上。统计数据表明，早期风电增速箱故障大多是由轴承引起的。对某企业部分增速箱进行试验后，发现由于轴承游隙的作用，增大了啮合轴的平行度误差，影响了啮合效率，产生附加噪声振动等，从而降低了齿轮的寿命。因此，轴承游隙及装配间隙的合理配置对于提高齿轮箱的寿命有重要作用。同时，轴孔的制造公差越小，装配效果越好，但同时也提高了制造成本。因此，对轴承游隙—轴套—轴孔的尺寸链进行多目标模糊稳健优化设计有重要意义。(www.xing528.com)

图2.14所示为某风电增速箱高速级的装配尺寸链，其中D1为轴承孔的直径，为轴套尺寸，为轴的直径，D3为考虑轴承游隙和装配间隙所预留的间隙尺寸。在保证D3为0.015～0.13 mm的条件下，按实用经验，该间隙最适宜的范围应为0.028～0.082 mm。优化目标为装配间隙D3及轴孔的制造公差。设计变量为轴孔直径D1、轴孔的制造公差。

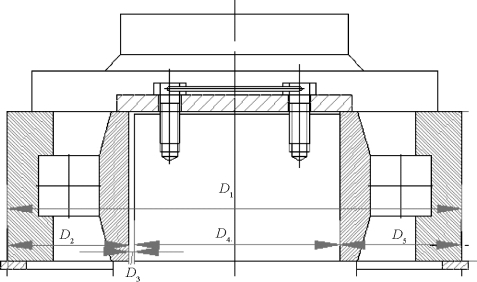
图2.14　风电增速箱高速级的装配尺寸链

解：设计质量指标y为轴向装配间隙A0，且

y=D3=D1-(D2+D4+D5)

y的设计目标为，其隶属函数采用梯形分布，其值在[0.15，0.30]内等于1，在[0.083，0.150]和[0.30，0.43]内呈线性分布，其他处的值为0。设尺寸链各组成环误差呈正态分布，A1的制造公差表示为±Δx，并控制该公差不小于9级精度的标准公差IT9，以保证箱体的制造工艺性。在控制废品率不超过0.1%时，取设计变量x1=A1，x2=Δx，则模糊稳健优化设计模型为

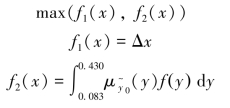
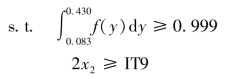
根据约束条件和设计者的经验确定方差和优质品率的偏好区间如表2.11所示。由三次插值法分别得到f1（x）和f2（x）的偏好函数，再由式（2.11）得到关于容许差和模糊优质品率的综合偏好函数。考虑各目标间的不同重要程度关系，设定模糊权值和各目标偏好函数的区间边界值如表2.10和表2.11所示。产品质量指标与设计变量容差指标均取越大越好，可设为1S型偏好函数。建立基于FWPP的模糊稳健优化模型，求解模型得到两种情况下的最佳调和解见表2.12。

表2.10　设定的模糊权值

表2.11　各目标偏好函数的区间边界值

表2.12　两种情况下的最佳调和解

结果比较可知，当两目标的权值取近似相等时，最终解与黄洪钟等人（2005）所提双目标物理规划方法所得结果基本一致。当降低成本目标的权值时，虽然成本略有上升，但产品质量明显改善，达到了由决策者提供不明确偏好下的稳健设计要求。决策者可以通过不断调整各目标的模糊权值，不断提高对原稳健设计问题的认识，从而实现局部偏好逐渐明确过程。