基于模糊相对重要程度关系的模糊赋权法优化

目前，文献中的权值确定方法种类众多，总体可分为主观赋权法和客观赋权法及其组合赋权法。客观赋权法[353-358]的特点是使用决策方案数据，利用优化方法计算权值，适用于具有客观准则相对重要程度关系数据的问题。主观赋权法[359-363]的特点根据决策者的偏好、经验和知识来构建比较矩阵来确定权重。

对于某一多目标决策问题，其目标函数记为F={f1，f2，…，fl}。目标间的相对重要程度关系可以用如下规则进行定义：

①f1不如f2重要；

②f1远不如f2重要；

③f1与f2同等重要；

④f1比f2重要；

⑤f1远比f2重要；

⑥f1和f2无关。

对于规则③、⑥所定义的关系，决策者一般能给出明确的判断；而其他规则所定义的关系，决策者就很难进行明确的定量描述。

对目标函数较多且具有决策者不明确偏好信息，不能对目标间相对重要程度进行精确量化的问题，采用正闭区间数来表达模糊判断是合理的且易被决策者接受的方式。具体处理方法如下。

（1）用确定关系对目标函数进行分类。可以把所有的目标函数分成两组：重要的和不重要的。对于不重要的那一组目标函数，在计算中可以忽略（或令其权重为一个极小值）。对于重要的一组目标函数记为F={f1，f2，…，fi}，利用关系≈构造m个等价类，其中Ci=F且Ci∪Cj=φ，i≠j，从每个等价类Ci中选择一个元素ci构成集合C={c1，c2，…，cm}，其中m≤i。

（2）利用模糊关系建立目标两两比较的模糊偏好矩阵。根据决策者对各目标间的相对重要程度的模糊判断，将各等价类间的关系定义为模糊数，则决策者的模糊偏好矩阵。考虑关系＜、≪、＞和≫的语气算子的模糊定量标度，将上述关系可描述为论域（0，1）上的三角模糊集（其中p=1，2，3，4），则对任意两个等价类重要性进行比较，可按表2.1确定。

表2.1　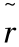ij与目标重要性对照表

表2.1中，0＜r1＜l2，r3＜l4，r4＜1（1-x）。对取α-截集可得到一系列的，当α取值一定时，目标等价类间两两比较的模糊偏好矩阵可表示为。根据ci、cj间关系对rij进行赋值，即

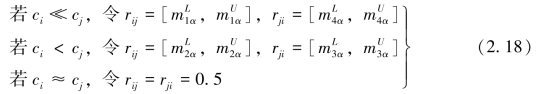
显然，rij与rji间的差值大小，表示决策者对该关系程度的偏好；而间的差值大小，则反映了决策者对该关系偏好的不确定度。当α=1时，表示决策者对该关系具有确定的偏好。

（3）α水平下，权重区间的计算。对于目标两两比较的偏好矩阵中分量为确定值的情况，关志华等（2002）给出了计算权重的公式及其理论推导过程。本书在该方法的基础上，推广了模糊权值的求解方法。

首先，利用下列公式求得各等价类Ci的模糊权重系数（wci）α，即

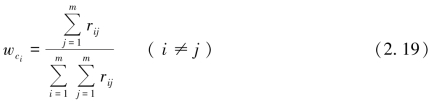
分别将两组参数代入式（2.19），得到wci1、wci2，分别对其进行规范化处理，得到wi1、wi2。最终多目标决策问题的权重可表示为

式中，。

例：对于有7个目标的多目标决策问题F={f1，f2，…，f7}，根据关系≈可以构造等价类：C1={f1，f2}，C2={f4}，C3={f5}，C4={f7}，故有：C={c1，c2，c3，c4}，假如决策者的偏好为：c1＜c2，c1＞c3，c1＞c4，c3≫c4。

根据决策者对各个目标函数的模糊偏好需求，建立关系＜、≪、＞和≫的模糊数表达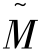p，设α分别取0.6，0.2。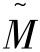p、（Mp）0.6、（Mp）0.2如表2.2所示。(www.xing528.com)

表2.2　模糊关系表达

建立模糊偏好矩阵，即

分别将代入上式，得到（wci）α如表所示。

表2.3　等价类的权值计算结果

由表2.3可知，在不同α水平下，都有（wc3）α＞（wc1）α＞（wc2）α＞（wc4）α，这与假设的决策者的等价类排序偏好符合。随着α水平的降低，与的差值增大，很好得体现了决策者偏好的不确定程度。

对（wci）α进行规范化，最终获得目标函数的权重集如表2.4所示。

表2.4　权值计算结果

（4）模糊权重的定量化处理。对区间折衷规划问题，当不同wi值从变化到时，将产生一系列fi在不同偏好下的有效解。如果权重集为wi在其区间均匀取值后的组合时，求解得到的满意解集可认为是原决策问题Pareto曲面上满意区域内均匀分布的点的集合。

设权重wi的取值区间为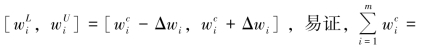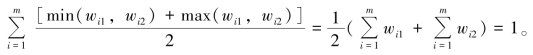将区间分为2n等份。。若令目标i个权重为

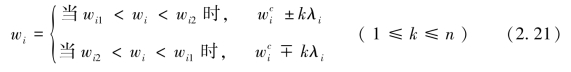
则有。

证明：对于任意在区间内取值的wi有

令wi按排序。将前（m-1）个wi在内按增量λi任意取值，得，其中-n＜α＜n。wm为待定，设。将wi的任意组合，建立被择权重向量集{w1，w2，…，ws}，其中s=（2n+1）m-1。被择权重向量集中任意向量的有效性可通过式（2.22）验证。即

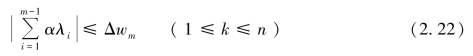
若式（2.22）成立，则该被择权重向量可行。令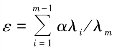，则wm也可确定。

上述过程可采用Matlab编程求解。例如，三目标决策问题的权重区间为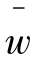1=[0.4，0.6]、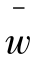2=[0.1，0.2]和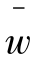3=[0.3，0.4]，各区间均取5个点，得到如图2.5所示的权重集。

图2.5　权重的增量变化

由此可见，基于上述规则的模糊权重量化处理方法，所获得的每个权重向量都是其分量在各自区间均匀取值后的组合。所建权重集能够最大化的保留原区间型权重所表达的不确定信息。当各目标权重取值范围和所选权重的个数确定，通过该方法即可获得确定且唯一的权重集。