优化物理规划模型：模糊加权物理规划（FWPP）

传统物理规划方法采用满意区间边界来定义准则内偏好，并通过OVO准则（物理规划认为某一设计目标从可容忍区间的较差边界改进到较好边界，优于所有其他的设计目标从满意区间的较差边界改进到较好边界，即OVO准则）来表达则设计目标间的偏好。其核心思想是认为某一设计目标从可容忍区间的较差边界改进到较好边界，优于所有其他的设计目标从满意区间的较差边界改进到较好边界。对于任意目标在同一满意区间内的偏好函数取值范围相同。而传统物理规划的综合偏好函数是以各目标偏好函数等权值的加权和形式给出的。这就意味着，决策者要根据各满意区间内目标的相对重要程度等同的原则来建立模型。虽然设置满意区间比给定权重的方式更直观，但多数情况下要精确给出各目标间同一偏好区间同等重要的先验信息，仍然是很困难的。因此，采用物理规划方法求解多目标问题时，通常还需要决策者不断调整满意区间边界值，以获得满意解。在此背景下，出现了一种能够将物理规划的内外准则分离处理的偏好函数构造方法，以解决上述问题。

（1）加权物理规划模型。假设对于某多目标优化问题，决策者同时具有以下两类偏好信息：

①各目标间的相对重要程度相对重要关系wp（p=1，…，nsc）信息；

②各目标相对独立时，仅考虑单一准则时各设计方案优劣的比较信息，并根据统计数据、常识或经验设定各满意区间tps（s=1，2，3，4，5）。

采用物理规划原理将这两类信息集成起来得到的决策者偏好结构，称为加权物理规划模型，权重模糊数时为模糊加权物理规划（FWPP）模型。传统物理规划模型可以看成是平均加权情况下的该模型的特殊形式（WAPP）。

根据所设定的满意区间建立各目标的偏好函数，将权值带入偏好函数并进行综合，采用各设计目标偏好函数的加权平均值的常用对数作为物理规划优化过程的综合偏好函数，得到加权物理规划最终的数学模型，即

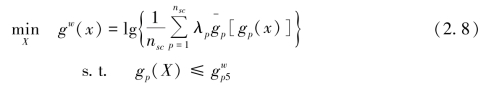
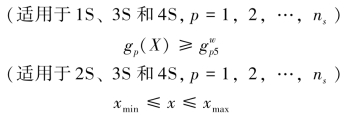
式中，λp为控制参数，λp=nscwp。

（2）WPP模型的转换。物理规划偏好函数的特性决定，对任意类型的偏好函数，在给定的两个相同满意程度区间（如满意区间-可容忍区间）交点处，偏好函数Zp的值相等。以1S型线性物理规划偏好函数为例。设目标gp的第s个满意区间的边界值tp，s-1、tps在WPP模型中对应的偏好值为，该段分段线性函数的斜率为。WPP模型与WAPP模型在相同满意程度区间对应的偏好函数值范围存在如下关系，即

由式（2.7）知，对于决策者事先设定的两个相同偏好区间在WPP模型中所对应的偏好函数值为λp的函数，当不同目标的λ值不等时，WPP模型就无法采用OVO准则求解。因此，简单套用WAPP模型形式是无效的，必须对WPP模型偏好结构参数进行适当的转换，以满足各目标值相等的偏好函数特性要求。转化的途径有两种：保持综合偏好函数形式不变，对偏好区间进行转换；或者偏好区间不变，将WPP模型中的目标函数映射到WAPP模型中。经推导得与gp、tps的转换关系为

将新的分别代入传统物理规划模型，则得到两种WPP模型的转换形式，其综合偏好函数为(www.xing528.com)

以1S为例，两种转换后的偏好函数与原偏好函数的关系如图2.4所示。考虑到目标值变换较为繁琐，为便于实际应用和降低问题的计算负担，通过变换偏好区间边界值的方式建立WPP模型较容易实现。从图2.4（a）中可以看出，的偏好值受wp取值的影响，各目标的Zs值无法保证一致。转换后的在函数形式上与传统物理规划的相同，只是偏好区间发生了平移，因此OVO准则适用于改进后的WPP模型。当λp＞1时，与相比的偏好区间整体向左平移，表示决策者提供了对该目标的偏好要求，平移幅度越大表明其可改进的空间越大，这与增大权重值的物理意义相符；当λp＜1时，效果相反。

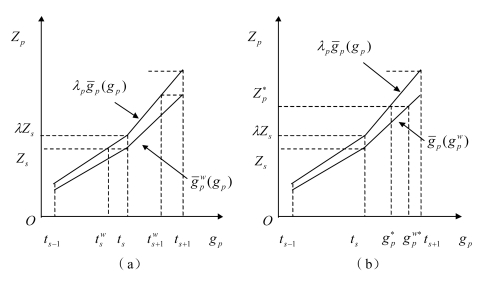
图2.4　偏好函数与原偏好函数的关系

综上所述，当偏好函数结构参数确定时，WPP模型与WAPP模型在偏好函数结构没有发生本质变化，两者之间存在仅受控制参数λp影响的转化关系，与目标值本身大小无关。决策者可以通过局部调整目标间相对重要关系来控制目标的改进与牺牲的方向和程度。彭旭等（2004）所提的通过调整偏好区间边界改变寻优方向的方法，没有考虑改进程度与目标间折衷性能的关系，因此寻优方向难以控制。另一方面，根据物理规划性质可知，物理规划得到的最优解可以达到有效域中的任意点。因此，加权物理规划模型既可以回避加权和方法无法达到有效域的非凸区域的缺点，而又继承了加权和法在表达和求解方面的简单性优势。

（3）模糊加权物理规划（FWPP）模型。设权重向量为时，令，则模糊加权物理规划（FWPP）的数学模型为

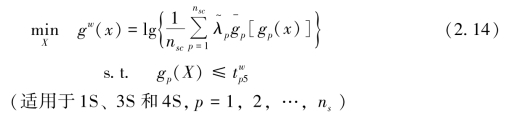
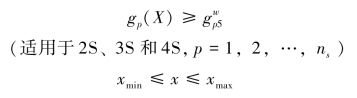
将代入式（2.7）中可得

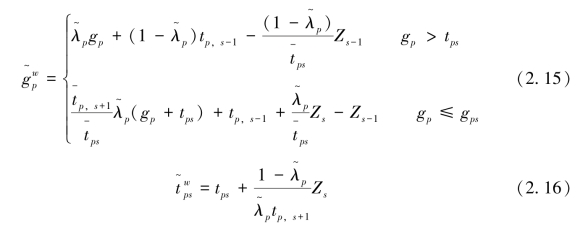
将分别代入式（2.12）和式（2.13），可得到模糊目标加权物理规划（FOWPP）模型和模糊偏好加权物理规划（FPWPP）模型，其偏好函数分别表示为。理论上来说，上述两个模型可采用前文所述的方法求解。但经过式（2.15）或式（2.16）的模糊运算后，的隶属函数形式较复杂，因此难以直接求解。采用Pareto解集削减方法则可避免这个问题。

当模糊权重的α-截集或模糊相对重要程度关系确定后，退化为区间数形式，记作，当不同wi值从变化到时，有控制参数λp=，i∈N，式（2.14）转换为

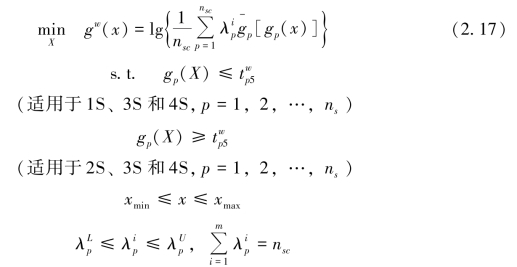
求解上述模型，将产生一系列gp在给定模糊权重置信水平限定的满意域范围内的不同偏好条件下的有效解。