基于FPPP模型的Pareto解集削减方法优化

当决策者具有不明确偏好信息时，具有模糊偏好的物理规划模型可有效地表达决策者的模糊偏好。当设计问题具有有限个设计方案时，可采用上文所提的排序方法求解FPPP模型。下面讨论当设计问题具有无限个设计方案时的FPPP模型求解方法。

FPPP模型中，模糊偏好区间边界值的定义为目标值域范围内的模糊子集，所有边界值在其取值范围内任意取值的组合所构造的偏好函数都包含在优化问题的模糊偏好结构中。由物理规划性质可知，所有这些偏好函数值所对应的解向量，都是多目标优化问题的一个Pareto解，而所有模糊偏好结构所限定的Pareto解将构成Pareto解曲面上的一个满意区域。为了获得这个满意区域的模型，首先将模糊偏好区间值明晰化处理，以获得该满意区间上的一系列Pareto解。

袁旭等给出了一种通过调整偏好区间边界改变寻优方向的方法。设定某一目标的寻优方向和精度后，可给出边界值的改进增量为dp，有dp即可得到新的偏好区间边界值。对于1-S型偏好函数，新的偏好区间边界值为

式中，tps为相应的原偏好区间边界值。

若要牺牲该目标，则

根据目标函数特性，还可采用缩放的方式确定新边界值。如可靠性目标，通常认为可靠度从0.9～0.999的改进比从0.8～0.9的改进意义重大得多。对于这类目标可采用下式确定其新的边界值，即

相对地，牺牲此目标有

根据这一思想，下面推导模糊边界值明晰化的公式。(www.xing528.com)

以模糊边界值为例，设在每个左右分别取n个值，连同共取2n+1个值。对，i∈n+1有

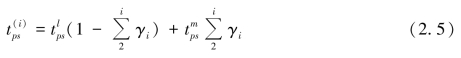
式中，γi为间的移动增量系数。γ1=0，当采用平移法平均取点时，γi=1/n，i=2，3，···，n。在上对称取值时，令γi=γ2n+2-j。根据模糊数学，边界值在附近取值的可能要远比在附近取值高，因此可通过设定γi增大在附近取值的密度。定义γi等差变化，，则

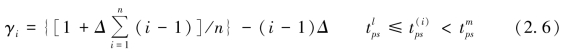
上述过程可通过Matlab编程实现，将计算获得的每个目标的2n+1个明晰边界值进行组合，可得到（2n+1）p-1个明晰型偏好函数。

例：双目标优化设计问题中，目标函数的某个偏好区间边界值分别为（10，12，15）、（0.4，0.6，0.7）。当采用平移法等差取点时，令n=4，Δ=0.1，则得到图2.3所示的明晰型边界值组合。

图2.3　明晰型边界值组合

当模糊边界值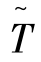的α-截集确定后，决策者可综合考虑感兴趣的区域，以及生成点密度与计算负担的平衡，设定γi和n。γi和n确定后，FPPP转换为如下形式。即

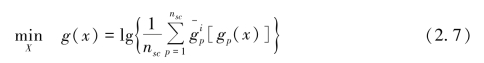
式中，为由第i组明晰型边界值构造的偏好函数，i∈2n+1。

求解上述2n+1个物理规划模型，将产生一系列gp在给定模糊边界值置信水平限定的满意域范围内的有效解。当各有效解间的距离满足决策者要求时，决策者在上述解集中所选的最满意解可视为多目标优化问题的最优解。