决策偏好结构表示决策者对于各优化目标,以及它们之间的折衷偏好。一个设计结果产生之后,设计者可以根据此结果的目标函数值向量来表达对于此设计结果的偏好信息,比如赋予此设计结果一个偏好值。偏好信息的确定过程见图2.1。
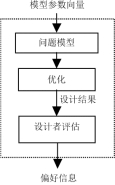
图2.1 偏好信息的确定过程
从图2.1中可以看出,模型参数向量是输入,而偏好信息是输出。设计者可以控制、修改模型参数向量以得到最佳满足其偏好结构的设计方案。建立决策者偏好结构模型的最直接办法是建立从目标函数向量到偏好信息之间的映射。权函数法、功效函数法、评价函数法、满意优化法和物理规划法的数学模型都可以看做是决策偏好结构。另外,许多文献都通过神经网络建立决策者的偏好结构模型[351-352]。对于这类优化方法,设计变量、目标函数和约束已经通过分析和建模确定了。这时候,设计者可以控制的只有模型参数向量。也就是说,对于一个具体的多目标优化问题来说,一旦模型参数向量确定了,通过计算可以得到唯一的优化结果。
当决策者的偏好信息不明确时,优化模型的参数向量可以表达为模糊形式,此时,上述优化问题的决策偏好结构就是模糊偏好结构,模糊偏好结构限定的最优解并非唯一,而是Pareto前沿面上的一个特定区域,称为Pareto前沿面满意区域。该区域虽然将决策者需要考察的Pareto解范围大大削减了,但决策者无法对它们一一考察,因此要用一组具有代表性的候选解代替该区域,从而使决策者能够提供该满意区域的局部偏好信息,最终从这有限个最优解中挑选出最满意解。根据模糊偏好结构的这一特点,本书给出的求解思路为:用一组具有代表性的候选解代替决策者对Pareto前沿面上感兴趣的区域,将模糊多目标优化问题转换为确定型多目标决策问题,进而根据决策者局部偏好信息对有限个备选方案进行评价,最终获得满意解。具体的求解过程如图2.2所示,其关键步骤如下。
(1)生成最小Pareto前沿面:建立多目标优化问题的数学模型,根据目标间性能折衷和决策精度要求,设定最小Pareto解之间的距离向量,采用PGA技术生成近似Pareto前沿面。(https://www.xing528.com)
(2)满意设计方案评价:建立模糊偏好结构,将决策者满意解限定到一定区域内,通过判断每个Pareto解是否落在该区域,生成备选方案集。由决策者提供其在Pareto曲面满意区域内的局部偏好,对备选方案集进行评价,得到最佳符合决策者局部偏好的Pareto解;若决策者无法提供局部偏好信息,可利用现有偏好信息在满意区域内进行折衷分析,得到调和解(Compromise Solution),供决策者参考。
(3)偏好结构调整:若备选方案集中没有决策者满意解,可通过修改模糊偏好结构的控制参数向量建立新的偏好结构,以调整满意区域在Pareto前沿面上的范围或位置,改进寻优方向;否则,改进原多目标优化问题的模型。重复上述过程,直至决策者满意为止。
显然,实施该优化设计过程的关键问题在于:如何建立具有代表性的备选方案集来表征Pareto前沿面满意区域,备选方案集应保证Pareto解不会遗漏或分布不均;决策者局部偏好如何表达。
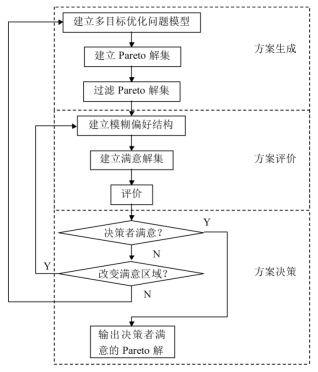
图2.2 基于模糊偏好结构的交互式优化设计的具体求解过程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




