多年来,传统的优化技术和方法已经成功地应用于求解一类具有清晰定义结构或行为的系统,这种方法一般称为确定型或清晰型优化方法,其基础是确定的数学模型和准确的数学方法。然而,多目标优化问题中,多个目标之间存在的矛盾冲突性和不可公度性使得优化所有目标存在很大难度,因此人们利用了模糊的概念来表征决策者对于解的满意程度,从而求解出最终解。此外,各种各样的模糊不确定性问题也是优化决策分析中存在的普遍现象,成了影响最后结果的关键问题之一。根据上述的模糊特性,就构成了多目标模糊优化问题。与单目标模糊优化问题一样,学者们从模糊变量的不同角度进行了研究。多目标模糊优化方法和模型众多,R.E.Stever(1983)根据多目标模糊优化方法所基于的理论基础和问题类型的不同对其进行了分类;将所有多目标模糊优化方法分为基于模糊子集理论的多目标优化方法和基于可能性理论的多目标优化方法,如图1.2和1.3所示。下面对其中的经典方法进行简要介绍。
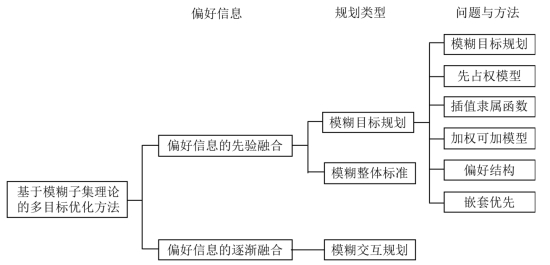
图1.2 基于模糊子集理论的多目标优化方法
(1)基于模糊子集理论的多目标优化方法。根据Zadeh(1965)的经典模糊子集理论,决策者对于每个目标的满意程度可以用隶属度函数值来表示,从而能够形成新的单目标优化问题,这已经成为学者们广为采用的一种策略。Zimmermann(1978)率先利用最大最小算子给出了关于多目标的模糊线性规划模型,开创了基于决策者满意度的多目标模糊优化的先河。在此基础上,满意度的概念得到了充分的利用,不同的隶属度函数形式和决策形式用来获得满意的结果,并在各种多目标优化问题中得到了广泛的研究和应用。(https://www.xing528.com)
(2)基于可能性理论的多目标优化方法。在模糊子集理论得到长足发展后,Kaufmann(1975)率先给出了模糊变量的概念,基于事件或事务发生可能性的模糊性,Zadeh(1978)提出了可能性理论,用可能性分布来进行刻画。根据可能性分布,相关的研究解决了有模糊系数的多目标优化问题。
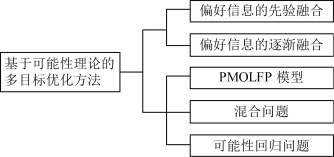
图1.3 基于可能性理论的多目标优化方法
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




