多目标优化方法的研究现状及进展

多目标优化也叫多指标优化或向量优化，可一般性地定义为在一组约束条件下，极大化（或极小化）多个不同的目标函数，其向量化的定义为：寻找一个由设计变量组成的向量，使它能够满足约束条件和由目标函数组成的向量函数。多目标优化的意义在于找到一个或多个解，使设计者能接受所有的目标值。

1896年，法国经济学家V.Pareto从经济学的角度率先提出了多目标决策优化问题，将许多本质上不可比较的多目标转化为单目标进行求解，首先提出了向量化的概念，即现在使用到Pareto最优概念，以后很长一段时间内对多目标优化决策没有取得有价值的研究成果。1944年，美籍匈牙利数学家、计算机之父、对策论的鼻祖Von Neumann等人从博弈论的角度提出具有多个决策者、又彼此互相矛盾的多目标决策问题，标志着近代意义上的多目标决策的诞生。1951年，美国经济学家T.C.Koopmans针对有限资源的合理分配活动和生产，提出了多目标最优化问题，并正式使用Pareto最优概念，首次使用有效向量概念，亦即现代多目标决策中的非劣解概念。同年，H.W.Kuhn和A.W.Tucker从数学规划的角度提出向量极大化问题和有效解存在的充分必要条件，建立多目标优化决策非劣解的理论基础，奠定了非线性优化技术理论的基础。1961年，Charnes1和Cooper提出了基于目标值和实际优化值之差的绝对值之和最小的目标规划方法。1963年，L.A.Zadeh从控制论的角度提出了多目标问题。由于多目标问题最早从经济学角度而引发的，因而评价多目标优化时，常常引入均衡论、社会福利理论、对策论等方法的概念并加以相应解释。20世纪70年代以后，多目标决策优化取得了较大发展。

常规多目标优化问题的一般形式为

式中　F（x）——优化模型的目标函数向量；

fj（x）——期望极小化的第j个目标函数，j=1，2，…，p；

gi（x）——第i个不等式约束函数，i=1，2，…，m。

多目标优化问题与单目标优化问题的一个本质区别是：优化的目标是一个向量函数。因此，在向量自然序的意义下，可以给出式（1.1）几类解的概念。

定义1.1　设x∗∈Rn，若对任意的x∈Rn及j=1，2，…，p，都有定义ft（x∗）≤ft（x）成立，则称x∗为多目标优化问题的绝对最优解。而F（x∗）=[f1（x∗），f2（x∗），…，fv（x∗）]T称为绝对最优值。

定义1.2　设x∗∈Rn，若不存在x∈Rn，满足F（x）≤F（x∗）成立，则称x∗为多目标优化问题的有效解（或者称为Pareto解，Pareto有效解，Pareto最优解），亦称为非劣解。

定义1.3　设x∗∈Rn，若不存在x∈Rn，满足F（x）＜F（x∗）成立，则称x∗为多目标优化问题的弱有效解（或者称为弱Pareto解，Pareto弱有效解），亦称为弱非劣解。

与单目标优化问题最优解不同的是，Pareto最优解虽然是多目标优化问题中合理的、可行的解，但其数量通常是众多的。然而在实际应用中，一般是希望最终得到唯一解。因此，为了从多目标函数的Pareto解集中选出特定的结果，必须设定评价标准（或决策规则），用以表示决策者对于目标空间中解的偏爱程度，这称之为偏好信息，由此所确定的解为满意解。如果缺少了偏好信息，面对众多的Pareto最优解，分析者就会感到无从下手，决策者也不能得到满意的结果，因此以输入形式给出的偏好信息起到了约束的作用，缩小了可行域的范围。作为多目标优化问题中至关重要的一个环节，决策者给出的偏好信息起着决定性的作用，是选择评价形式的依据，不同的评价标准可能给出不同的Pareto最优解。因此，根据Huang等于1979年提出的划分原则，可以按照偏好信息的表达方式，将多目标优化算法大致分为以下3类：

（1）事前索取偏好信息。在优化之前，决策者事先一次性提供全部的偏好信息。属于这一类的求解多目标优化问题的方法有总体准则法、效用函数法、有界目标法、字典序法、目标规划法、目标达到法等；

（2）逐步索取偏好信息。在优化过程中，由分析人员通过对话的方式向决策者逐步获取偏好信息。属于这一类的方法有逐步进行法、多目标问题的序贯解法、Geoffrion法、代理权衡法、移动理想点法、满意目标法等；

（3）事后索取偏好信息。在优化之后，由分析人员求得全部或大部分非劣解后，再请决策者在非劣解集中选择。属于这一类的方法有参数法、多目标线性规划法、自适应搜索法等。

下面根据Huang的分类方法简要地介绍事前索取偏好信息的多且标优化方法。

1.事前索取偏好信息的多目标优化方法

（1）约束法。根据设计者的偏好，选择一个参考目标，如fk0，而要求其他（m-1）个目标函数满足一定的约束要求即可。具体地，有

式中，参数εk为设计者事先给定。约束法也称ε约束法。约束法求得的最优解只能保证是原多目标优化问题的Pareto弱有效解。对于任一个Pareto解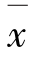，都存在一组参数εk（k=1，2，…，m，k≠k0），使得为相应的参数设置下用约束法求得的最优解。约束法重点保证第k0个目标的效益，同时又适当照顾其他目标，这在许多实际设计问题的求解中颇受设计者的偏爱。

（2）分层序列法。根据各目标的重要程度不同，将m各目标函数排序。假定f1最重要，f2次之，依此类推，fm最不重要。逐次求解下列m个单目标优化问题（Pk）的最优解xk，其中

用分层序列法求得的解是原多目标优化问题的一个Pareto有效解。分层序列法还融合了设计者进一步的偏好信息。但它也存在不足之处，一是求解一个Pareto解需要求解m个优化问题，另一方面在不少场合设计者拒绝将m个目标进行排序。

（3）评价函数法。对于一个多目标规划问题，如果能根据设计者提供的偏好信息构造出一个实函数，使得求解设计者最满意的解等价于求解以该实函数为新的目标函数的最优解，则称该多目标问题是可标量化的，多目标效用理论就是研究这样的实函数存在的条件和如何构造问题的。多目标效用理论的基础是：假定设计者的偏好可以用一个称为效用函数的实函数来表示。一旦效用函数能够被构造出来，则方案的最后选取即按效用函数值来决定：在确定的场合下，选取效用函数值最大的方案；在不确定场合下，选取期望效用函数值最大的方案。虽然效用理论为多目标优化分析提供了一种工具，但在许多场合下，设计者所提供的偏好信息不足以确定这样的效用函数，估计或构造一个实际问题的效用函数是相当困难甚至是不可能的。

为了帮助设计者选择满意的解又克服多目标效用理论存在的困难，于是出现了评价函数的概念。评价函数是用来整体或局部逼近设计者心中常常是朦胧而难以构造出来的多属性效用函数，以评价方案的好坏。它的基本思想是：针对多目标优化问题，构造一个评价函数h[f（x）]，然后求解问题(www.xing528.com)

用该问题的最优解作为多目标优化问题的最优解。常用的评价函数法有加权系数法（线性加权法）、理想点法、平方和加权法、乘除法（费效比法）等，其中加权系数法和理想点法是最重要也是当前应用最广的两种多目标优化方法。

1）加权系数法。对多目标优化问题的m个目标按其重要程度给以适当的权系数λi≥0（i=1，2，…，m），且。然后求解下面的线性加权问题，即

用加权系数法求得的解是原多目标优化问题的一个Pareto有效解。加权系数法比较简单，其应用也非常广泛。但缺点是权重系数没有实际的物理意义，在实际应用中难以合理地确定；而且如果多目标优化问题的有效域是凹有效域，则利用加权系数法不能得到所有的Pareto有效解。

2）理想点法。理想点法就是求距离某个给定的理想点在某种范数意义下距离最短的可行解，即在X中寻找使f（x）与偏差最小的点x。一般情况下其中k=1，…，m。常用的描述偏差的函数有：

①p模函数，其中，1≤p≤±∞；

②极大偏差函数，；

③几何平均函数，。

权系数λi≥0（其中i=1，2，…，m）由设计者设定。

以p模函数或几何平均函数作为目标函数的理想点法求得的最优解是Pareto有效解，以极大偏差函数作为目标函数的理想点法求得的最优解是Pareto弱有效解。应用理想点法，可以得到所有的Pareto有效解。

由于极大偏差函数是不可微的，直接求解它会有困难。通常改求与它等价的下述问题，即

式（1.6）求解多目标优化的方法又称加权Tchebycheff法。

（4）增广加权Tchebycheff法。理想点法中的加权Tchebycheff法后来又推广得到增广加权Tchebycheff法（Augmented Weighted Tchebycheff Programs，AWTPs），并以其良好的性能得到广泛的应用。AWTPs的数学模型为

式中，ρ是一个很小的正数；zidea1表示理想点，即是求解以第i个设计目标作为目标函数，并以x∈X为约束的单目标优化问题得到的解的目标函数值。λi是设计目标i的权重，满足λi≥0，i=1，2，…，m。是最劣点，满足=min{ei|e∈N}，其中N表示Pareto曲面。在实际应用中，通常用Messac（2002）所述的方法评估得到。

2.逐步索取偏好信息的多目标优化方法

逐步索取偏好信息的多目标优化方法也称交互式多目标优化方法，是近年来应用日趋广泛的一类解决多目标优化和多目标决策问题的方法。这类方法无需设计者在一开始就提供他可能无法提供的有关问题的整体信息，只需在每一个具体方案结果上给出局部偏好信息。由于求解过程是交互式的，设计者在求解过程中可以对决策问题有愈来愈多和深刻的了解，因此最终求得的解也就比较符合他的偏好。其经典的求解思路简要介绍如下。

（1）逐步宽容约束法：在求解过程的分析阶段，分析者按照理想点法对模型求解，把得到的解所对应的一组参考目标值和问题的一组理想目标值一起提供给决策者参考；在决策阶段，决策者在比较由分析阶段求得的一组参考目标值和理想目标值的基础上，对已满意的目标给出使其目标值做出让步的宽容量，以换取不满意目标得到改善，再把这些信息提供给分析者继续求解。如此反复逐步以满意目标的宽容让步换取不满意目标的改善，最后求得决策者对各个目标均满意的解。

（2）权衡比替代法：假设问题中存在一个隐含的评价函数，利用这个隐含的评价函数的某些可求的局部信息，由决策者对需要比较的目标两两权衡其得失代价后，逐步调整，最后求得问题的满意解。

（3）逐次线性加权和法：加权系数不是事先给定，而是在求解过程中由决策者根据所获得的有关信息和对问题的偏好，逐步调整而趋于满意。

3.事后索取偏好信息的多目标优化方法

在现实的多目标优化问题中，由于决策者个人能力或决策环境所限，决策者有可能无法提前给出偏好信息或者无法在优化过程中根据局部结果判断给出。针对这种情况，一般是先利用某种优化算法对原无偏好的多目标优化问题进行求解，产生包含大量Pareto最优解的解集，然后根据这个集合中解的特点，由决策者给出偏好信息，最后挑选满意结果，这就形成了后验偏好信息。

在这类优化问题中，如何产生大量Pareto最优解是个很重要的步骤。因为这类优化方法对决策者的要求很少，决策者只需做到的就是在大量解中选择令其满意的解，如果不能用有效的算法生成能覆盖整个优化问题全部特性的解，那么就会给决策者对问题的认识带来偏差。如果这类优化方法存在局限性，那么就有可能会遗漏比较重要的解。此外，由于决策者直接从这些解中挑选最终解，局部决策偏好结构的合理性是影响最终优化效果的关键步骤。再者，由于待产生解的数量可能比较多，因此本类优化算法的计算量也是需要考虑的。为了得到能够包含优化问题所有特性的Pareto最优解集，目前常用的方法有简单加权和法、ε约束法、Pareto GA法和物理规划法等。