如何处理偏好信息的不确定性和不明确性？

随着人类改造自然和认识自然的不断深入，设计决策的难度也不断加大。在工程优化实践中，经常会碰到许多的不确定性现象。由于实际工程系统内部结构和机理的复杂性、设计目标的多样性、设计目标之间矛盾性等，以及由于人对客观事物认识上的局限性，不能够完全掌握事物运动发展的规律，因而在人的主观和客观两方面都存在许多不确定性。工程系统设计中不确定信息的主要来源有如下几种。

①试验分析带来的不确定性，如试验条件与实际系统所处的自然条件不完全一致而产生的不确定性，试验手段受客观条件的限制而造成测试结果的不完全正确所产生的不确定性等。

②统计分析带来的不确定性，如用有限的试验样本代替无限样本所产生的不确定性等。

③简化假设带来的不确定性，如力学分析、结构分析等中的简化假设而产生的不确定性等。

④人为错误带来的不确定性，如采用不正确的计算模型，分析计量中的错误，设计中的差错，制造中的疏忽等所带来的不确定性。

⑤未知因索带来的不确定性，如一些对系统的有影响但还未被人们认识的因素所产生的不确定性。

1.模糊集合的基本定义和运算法则

工程设计中造成信息不确定性的原因虽然很多，但从存在的范畴角度来定义，其均具有的属性为：不确定性因素是否是所研究事物表现出来的客观存在；设计者根据已有的知识水平和决策能力是否有能力对该不确定性因素给出明确的主观评价。信息本身的确定或不确定属性无所谓好坏，关键在于怎样去认识和把握确定和不确定属性反映出来的事物变化发展过程中必然与偶然、清晰与模糊、精确与近似之间的规律性。

Dubois（1985）从知识结构的角度对上述不确定信息进行分类，如图1.1所示。即“我们所掌握的关于某种情况的知识通常是不完美的，或者对知识的正确性存在疑惑（知识是不确定的），或者我们难以清楚地表达（知识是不明确的），这两种知识上的不完美经常是密不可分的。”根据该观点，知识的不完美包含人对环境不完整性的理解所造成的不确定性，以及人的思维和行为中以非随机性的认知现象为特征的不明确性。不确定性信息建模的主要数学工具是概率论和可能性理论；而不明确性信息建模的主要数学工具是模糊子集理论。

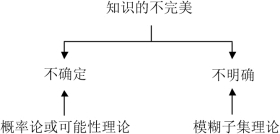
图1.1　不确定性和不明确性的区别

实际工程系统设计中，信息不确定性主要表现为随机性。随机性是由于因果关系的不明确而形成的试验结果的不确定性，亦即由于条件不充分，使得在条件与事件之间不能出现决定性的因果关系，导致在事件的出现与否上表现出的不确定性，因而它是因果律的一种破缺。由于现实世界及工程系统的复杂性，不可能对所有的因果关系都认识到并能够加以控制。因而，对于未来发生的事物无法严格控制其发生的条件，一些偶然因素使事物发展的结果不可能准确地预先知道，这种由于条件的不确定性和因果关系不明确而形成的后果的不确定性称为随机性。随机性是当任何一个具有随机性的事物，一旦结束或试验完成，必然得到确定性的结果，而不再具有任何不确定性。因此，随机性是一种外在因果的不确定性，随机性只针对未来将要发生的事物，现在的和已发生的事物都不具有随机性。从信息论观点出发，随机性指涉及信息的量。

自从Pascal和Fermat首先应用概率论来处理的不确定性信息以来，主观概率、数理统计和随机过程等的理论和方法所构成的泛概率论被逐渐开展，用以描述和处理各种逻辑演绎、统计归纳和不确定程度等情况，从随机性中去把握广义的因果规律。可能性理论是L.A.Zadeh于1978年提出的，他从模糊集合的隶属函数中定义了可能性测度，以衡量事件可能发生的程度的主观判断和客观衡量。根据其功能，可以看出可能性理论实际上是概率论在某些情况下的替代方法。

Chen（1992）将不明确信息分为4类：不可量化的信息（个人的主观判断）；不完整的信息；涉及较高成本的信息（获取成本、处理成本、转化成本等）；部分被忽略的信息。实际工程系统设计中，信息不确定性主要表现为模糊性。模糊性是由于概念本身没有明确的外延，一个对象是否属于某一概念难以判定，从而不可能给某事物以明确的定义和评定标准。随着科学技术的深入发展，工程系统越来越大而且越来越复杂，需要人们研究的变量越来越多且变量间的关系也越来越复杂，对系统的描述和处理的精确性要求却越来越高。然而，通常复杂性和精确性将相互排斥。当系统复杂性增加时，我们对信息精确化能力将减弱，复杂性意味着因素众多，以致人们只能把研究对象适当简化或抽象成模型，忽略掉次要部分，这就使得本来是明确的概念变得不明确起来；同时，复杂性还意味着深度的延长。对系统处理过程中的误差积累，也可能使不明确性变得不可忽略。(www.xing528.com)

2.优化设计中的不明确偏好信息

从优化建模与分析过程来看，不明确信息表现为：

（1）设计要求的不确定性：如系统响应允许范围、失效准则，以及设计方案的好坏标准等，都会受到人的主观因素的影响，从而影响优化模型的建立和最终的优化设计结果。其对应的不明确信息分类为不可量化的信息。

（2）输入参数的不明确性：即进行分析所必要的输入参数（包括设计变量和设计参数）的变差，如结构尺寸的加工和测量误差、结构材料特性的制造误差，以及结构所受荷载的波动等。其对应的不明确信息分类为不完整的信息。

（3）分析模型的不明确性：是指算法或仿真软件本身所产生的不确定性。主要有三方面的因素，其一为仿真软件在开发过程中所依据的科学理论带来的误差，大多数科学理论只是对工程实际的近似反映，如结构分析中普遍采用的梁的平面假设，以及板壳的各种近似模型等，其分析结果与试验结果相比，总有一定误差，基于这些近似理论所开发的软件，其仿真结果无疑也是近似的；其二为在使用这些软件时，所做的一些必要假设和近似所带来的误差，如用有限元进行结构分析时，所划分网格的疏密、边界条件的处理等带来的种种误差；其三为计算过程中的算法误差，如数值圆整误差、算法收敛准则等带来的计算误差。其对应的不明确信息分类为涉及较高成本的信息、部分被忽略的信息。

任何工程产品的设计都会面临上述不明确信息，必须在设计过程中对这些信息加以妥善处理。直接的解决办法是尽量减少或消除这些不确定因素，如提高产品的加工精度和测量精度、采用更准确的分析理论等，但这样不但会增加产品的设计成本和制造费用，而且显然也不可能完全予以消除。所以，合理的解决办法是在设计阶段对这些因素予以充分考虑和定量处理，从而提高产品抵抗各种不确定因素影响的能力（“容差”能力），即研究“决策信息不明确的多目标优化设计”理论，其研究的理论基础为模糊子集理论。

3.模糊子集理论在决策信息不明确的优化设计问题中的应用

模糊子集理论适合处理的问题主要是具有较强主观性且难以进行概率分析的不明确性。不明确信息可通过模糊区间加以表达，以实数集为参照，集合的模糊子集，构成了数量与不明确性间的沟通方式；模糊数据的集成是模糊效用理论的延伸；模糊决策方法为消解信息的不明确性提供了有效途径。

从数学规划方法角度来看，模糊多目标决策是多目标决策的模糊版延伸。理论上，模糊多目标决策分析一般分为两步：一是在多目标决策基本步骤基础上集成备选方案的模糊结果；二是依据结果对备选方案进行模糊排序。其中第一步是多属性价值理论的模糊化版本，第二步是模糊处理的直接结果，也就是对模糊结果的比较或解模糊。这种两步分类法实际上忽略了对模糊表达形式选择的深入分析，而正是对模糊表达方式的选择问题连接了不明确性知识和数学规划模型，作为工程实际与理论模型间的连接点，模糊表达方式的选择构成了过程的重要步骤。所以，可以认为尽管模糊多目标决策分析的应用呈多样性，其在决策信息不明确的优化设计问题时，基本应用方法可以归纳为3个步骤：

（1）定义在考虑和观察对象的不明确性、精确度灵活横流的难度抑或不可能性。在多目标决策的框架中，对不明确性的处理往往通过模糊区间和几何形状的渠道。当涉及对专家知识的表达时，这一步实质上是针对不明确性从认知角度确定模糊算法应用可能性的关键步骤。在概率论的范畴中经常使用的方法是主观概率；模糊区间在这方面的优势主要是不强求历史数据和案例，强调与主观判断之间的关系。这样的逻辑可以将专家通过仅有的相似度不高的案例建立起来的对新事物的判断进行量化处理；在历史数据和客观信息缺乏的情况下，以相对友好的界面进行定量处理。常用的模糊区间的几何形式有三角形和梯形等。

（2）在选择模糊表达方式的基础上对模糊区间进行运算。由于在多目标决策模型中，在计算的规范性上与模糊区间的公式运算相比较弱，所以算子的选择相对自由，基本原则是由Zadeh提出并由Dubois和Prade进一步发展的延展原则。

（3）对集成的模糊结果进行比较或解模糊。而在解集连续情况下，通常为数学规划方法。

显然，不确定性和不明确性都是工程系统设计中存在的客观实际问题。只有正确地、科学地处理，才能合理地描述工程系统及其设计过程，反映其实际规律，大大提高工程系统设计的有效性和实用性。设计过程中决策者所提供的偏好信息既包含决策者主观偏好、喜恶等自身的主观意识，也包含一定客观的衡量标准（如公理、准则、理论、实践经验等）。因此，复杂工程系统中，偏好信息可能具有不明确性和不确定性。本书主要采用模糊子集理论来研究多目标优化设计中的不明确偏好信息建模和决策问题。

如前所述，决策信息不明确下的工程分析和设计是十分活跃的研究领域，己有的理论与方法众多，此处不可能一一述及。本章仅介绍一些较成熟的、有代表性的理论，重点介绍各自的主要特点，而对其方法的细节不加详述。