有限差分技术简介

有限差分技术的物理基础仍然是能量守恒定律，计算时将所研究区域划分成离散网格（差分网格）或网格节点（差分节点），以相邻节点上函数值的差商代替偏微分方程中的微商，以这些离散点上近似值组成的代数方程组（差分方程组）来逼近偏微分方程从而得到离散点上的函数值。有限差分技术的基本问题有：

1）具有各种精度和各种功能的差分格式构造法。

2）差分方程的相容性、收敛性和稳定性。

3）差分方程的解法。

对不同类型的问题侧重点也不同。椭圆型方程主要是差分格式及其解法，对双曲型和抛物型方程首先是收敛性和稳定性问题。

由于计算机只能执行算术运算和逻辑运算，因此就需要一种用算术运算来处理函数微分运算的数值方法。而有限差分技术就是用离散网格点上的函数值来近似导数的一种方法。

设有x的解析函数y=f（x），从微分学知道函数y对x的导数为

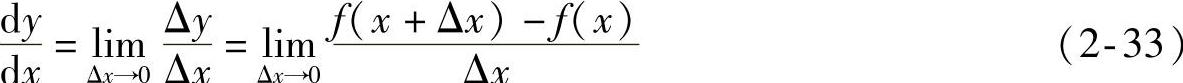
dy、dx分别是函数及自变量的微分，dy/dx是函数对自变量的导数，又称微商。相应地，式（2-33）中的Δx、Δy分别称为自变量及函数的差分，Δy/Δx为函数对自变量的差商。在导数的定义中Δx是以任意方式逼近于零的，因而Δx是可正可负的。在差分方法中，Δ_x总是取某一小的正数。这样一来，与微分对应的差分可以有3种形式：

向前差分

Δy=f（x+Δx）-f（x）（2-34）

向后差分

Δ_y=f（x）-f（x-Δx）（2-35）

中心差分

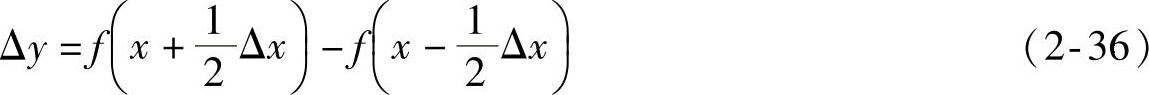
上面谈的是一阶导数，对应的称为一阶差分。对一阶差分再作一阶差分，就得到二阶差分，记为Δ²y。以向前差分为例，有

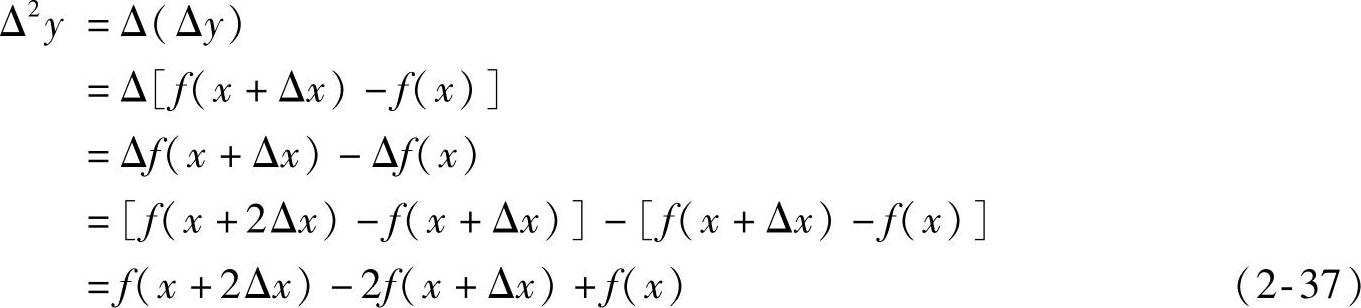
依次类推，任何阶差分都可以由低一阶再作一阶差分得到。

函数的差分与自变量的差分之比，即为函数对自变量的差商。如一阶向前差商为

一阶向后差商为

一阶中心差商为

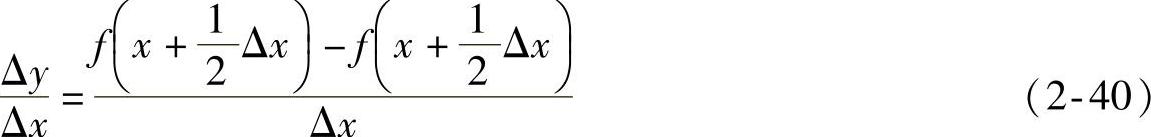
或(www.xing528.com)

二阶差商多取中心格式，即

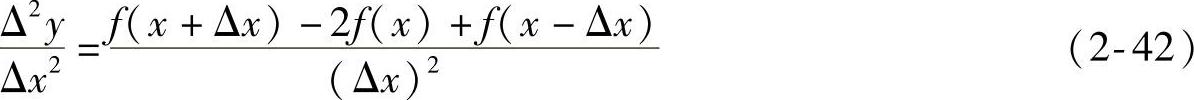
差商与导数的关系如图2-26所示。

由导数（微商）和差商的定义知道，当自变量的差分（增量）趋近于零时，就可以由差商得到导数。因此在数值计算中常用差商近似代替导数。差商与导数之间的误差表明差商逼近导数的程度，称为逼近误差。由函数的Taylor展开可以得到逼近误差相对于自变量差分（增量）的量级，称为用差商代替导数的精度，简称为差商的精度，其详细论述请参阅相关资料，本书这里不作赘述。

差分相应于微分，差商相应于导数。只不过差分和差商是用有限形式表示的，而微分和导数则是以极限形式表示的。如果将微分方程中的导数用相应的差商近似代替，就可以得到有限形式的差分方程。现以对流方程式（2-43）为例，列出相对应的差分方程。

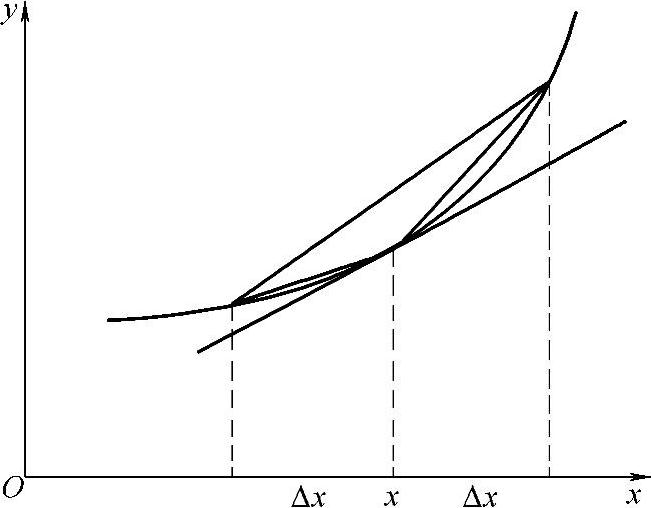
图2-26 差商与导数的关系

用差商近似代替导数时，首先要选定Δx和Δt，称为步长。然后在Oxt坐标平面上用平行于坐标轴的两族直线

x_i=x₀+iΔxi=0，1，2，…

t_n=nΔtn=0，1，2，…

划分出矩形网格，如图2-27所示。这里Δx和Δt取常数。直线t=t_n称为第n层，网格交叉点称为结点。

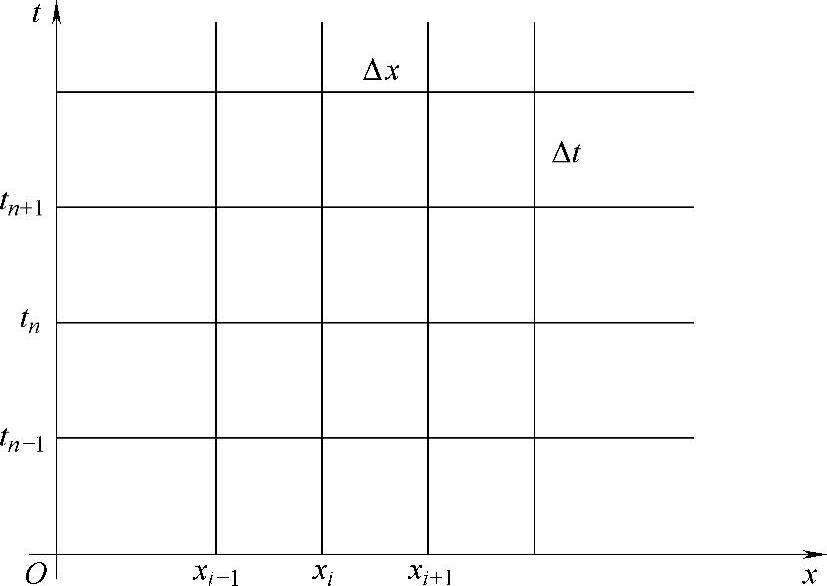
图2-27 网格划分

网格点划定后，就可针对某一结点，如图2-27中的结点（x_i，t_n），用差商近似代替导数。现用0ⁿ_i表示括号内函数在（x_i，t_n）点的值，则对流方程在该点为

如果时间导数用一阶向前差商近似代替

空间导数用一阶中心差商近似代替

则对流方程在（x_i，t_n）点对应的差分方程为

在有限差分法的具体运算中，计算误差总是不可避免的，如舍入误差，以及这种误差的传播、积累。如果这一误差对以后的影响越来越小，或这个误差保持在某个限度内，那么就称这个差分格式在给定的条件下稳定。