有限元技术在材料加工领域应用及解决热传导问题的思路与步骤

有限元技术是随着计算机的发展而迅速发展起来的一种现代计算方法。它是20世纪50年代首先在连续体力学领域——飞机结构静/动态特性分析中应用的一种有效的数值分析方法，随后很快广泛地应用于求解热传导、电磁场、流体力学等连续性问题。在材料加工领域，特别是模具行业，有限元技术的应用也越来越广泛。

有限元技术的基本思想是将连续的求解区域离散为一组个数有限且按一定方式相互联结在一起的单元的组合体。由于单元能按不同的联结方式进行组合，且单元本身又可以有不同形状，因此可以模拟出几何形状复杂的求解域。有限单元法作为数值分析方法的另一个重要特点是利用在每一个单元内假设的近似函数来分片地表示全求解域上待求的未知场函数。单元内的近似函数通常由未知场函数或其导数在单元的各个结点的数值和其插值函数来表达。这样一来，在有限元分析中，未知场函数或其导数在各个结点上的数值就成为新的未知量（也即自由度），从而使一个连续的无限自由度问题变成离散的有限自由度问题，一经求解出这些未知量，就可以通过插值函数计算出各个单元内场函数的近似解，从而得到整个求解域上的近似解。很显然，随着单元数目的增加，也即单元尺寸缩小，又或者随着单元自由度的增加及插值函数精度的提高，解的近似程度将不断改进。如果单元满足收敛要求，则近似解最后将收敛于精确解。

本节以热传导问题为例来说明有限元技术的解题思路和步骤。在压铸工艺中，温度对铸件的充型、凝固及压铸模的影响很大，常常需要在充型、凝固及冷却过程中进行温度场的分析，即分析热传导问题。

1.热传导方程与换热边界

物体内部的温度分布取决于物体内部的热量交换，以及物体与外部介质之间的热量交换，一般认为是与时间相关的。物体内部的热交换采用以下的热传导方程（Fourier方程）来描述

式中 ρ——密度（kg/m³）；

c——比热容[J/（kg·K）]；

λ_x、λ_y、λ_z——热导率[W/（m·k）]；

T——热力学温度（K）；

t——时间（s）；

Q——内热源密度（W/m³）。

对于各向同性材料，不同方向上的热导率相同，热传导方程可写为以下形式

除了热传导方程，计算物体内部的温度分布，还需要指定初始条件和边界条件。初始条件是指物体最初的温度分布情况

T_t=0=T₀（x，y，z）（2-14）

边界条件是指物体外表面与周围环境的热交换情况。在传热学中一般把边界条件分为三类。

1）给定物体边界上的温度，称为第一类边界条件。

物体表面上的温度或温度函数为已知，即

或

2）给定物体边界上的热量输入或输出，称为第二类边界条件。已知物体表面上热流密度，即

或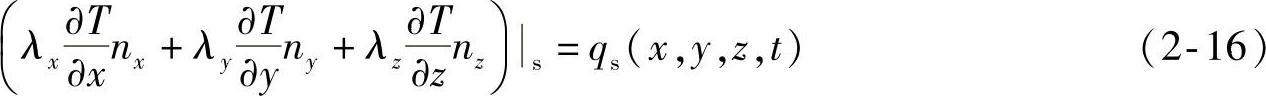

3）给定对流换热条件，称为第三类边界条件。

物体与其相接触的流体介质之间的对流传热系数和介质的温度为已知，即

式中h——传热系数[W/（m²·K）]；

T_s——物体表面的温度（K）；

T_f——介质温度（K）。

如果边界上的换热条件不随时间变化，物体内部的热源也不随时间变化，在经过一定时间的热交换后，物体内各点温度也将不随时间变化，即

这类问题称为稳态（Steady State）热传导问题。稳态热传导问题并不是温度场不随时间变化，而是指温度分布稳定后的状态，不关心物体内部的温度场如何从初始状态过渡到最后的稳定温度场。随时间变化的瞬态（Transient）热传导方程就退化为稳态热传导方程，三维问题的稳态热传导方程为(www.xing528.com)

对于各向同性的材料，可以得到以下的方程，称为Poisson方程

考虑物体不包含内热源的情况，各向同性材料中的温度场满足Laplace方程

在分析稳态热传导问题时，不需要考虑物体的初始温度分布对最后的稳定温度场的影响，因此不必考虑温度场的初始条件，而只需考虑换热边界条件。计算稳态温度场实际上是求解偏微分方程的边值问题。温度场是标量场，将物体离散成有限单元后，每个单元结点上只有一个温度未知数。

2.稳态温度场分析的一般有限元列式

为简化计算，这里采用加权余量法（Weighted Residual Method）建立稳态温度场分析的有限元列式。先把由无限个质点构成的结构，假想地划分成有限个简单形状的单元，简称为离散化（Discrete）。用这种有限个单元组成的离散化模型代替原来的物体，各个单元靠结点相连，单元之间的温度靠结点传递，称为单元结点温度，一般用{T}^e表示。单元的划分和结点的选择，除了根据结构的特点，计算精度的要求，以及考虑计算机的容量外，很大程度上是人为的。结构被离散后，首先对其中的各个单元进行传热分析，假定单元的形函数为

[N]=[N₁N₂…N_n]（2-21）

单元结点的温度为

{T}^e=[T₁T₂…T_n]^T（2-22）

单元内部的温度分布为

T=[N]{T}^e（2-23）

在一个单元内的加权积分公式为

由分部积分得

应用Green定理，一个单元内的加权积分公式写为

采用Galerkin方法，选择权函数为

w₁=N_i

将单元内的温度分布函数和换热边界条件代入式（2-25），单元的加权积分公式为

换热边界条件代入后，在式（2-26）内相应出现了第二类换热边界项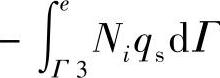Γ，第三类换热边界项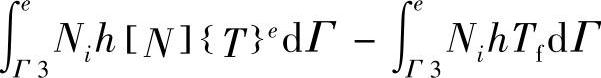，但没有出现与第一类换热边界对应的项。这是因为，采用N_i作为权函数，第一类换热边界被自动满足。写成矩阵形式有

式（2-27）是n个联立的线性方程组，可以确定n个结点的温度T_i。按有限元格式将式（2-27）表示为

K^eT^e=P^e（2-28）

其中，矩阵K^e为单元的导热矩阵或称为温度刚度矩阵；T^e为单元的结点温度向量；P^e称为单元的温度载荷向量或热载荷向量（Thermal Load Vector）。对于某个特定单元，单元导热矩阵K^e和温度载荷向量P^e的元素分别为

如果某个单元完全处于物体的内部，则

在整个物体上的加权积分方程是单元积分方程的和

根据单元结点的局部编号与整体编号的关系，直接求和得到整体刚度矩阵，整体方程组为

KT=P（2-32）

这些关系式构成一个线性方程组。引入边界条件后，求解这个线性方程组就可以得到基本未知量的解，根据所得到的解，再求出各个单元各个节点的温度。