数表与线图的程序化处理技巧

1.数表的程序化

工程中的数表有两类：一类是记载设计中所需的各种数表，如各类材料的力学性能、物理性能等，这些数据之间彼此没有明显的关系；另一类是列表函数，用以表达工程中某些复杂问题参数间的关系。由于复杂问题通常难于用理论公式准确表示，而是通过实验观察或用简化公式计算后，再根据经验加以修正，因此是一些离散的数据，可表示为

y_i=f（x_i）i=1，2，3，…，n（2-7）

式中，x_i与y_i的对应关系可组成一张表，称为列表函数。

数表的程序化是指将数表中的数据直接编入程序中。这种方法处理的数表在本质上与设计手册中的数表没有什么区别，只是做了方便程序检索或调用的处理。从理论上讲，数表或列表函数已经是结构化了的数据，一维数表、二维数表或多维数表分别与计算机算法语言的一维数组、二维数组或多维数组相对应，很容易通过程序进行赋值和调用。

2.数表的公式化

上述对数表的存储和使用，由于数据的离散性和数量有限，在相邻两数值点之间只能取相近的数据。这无疑会给计算结果带来误差。因此，对于数据间有某种联系或函数关系的列表函数，应尽量进行公式化处理。常用的方法有两种：函数插值和数据拟合。

（1）函数插值　插值的基本思想是：设法构造一个函数y=p（x）作为列表函数的近似表达式，然后计算p（x）的值以得到f（x）的值，最常用的近似函数类型为代数多项式。代数插值的数学含义可表述如下：设y=f（x）是区间[a，b]上的连续函数，已知它在[a，b]上的几个互不相同的点x₁，x₂，x₃，…，x_n上的函数y₁，y₂，y₃，…，y_n。若代数多项式p（x）满足p（x_i）=y_i，（i=1，2，…，n），则称p（x）为函数y=f（x）的插值多项式，x₁，x₂，x₃，…，x_n为插值节点，区间[a，b]为插值区间，y=f（x）称为差值函数。

（2）数据拟合 一般列表函数的数据是通过试验所得的，不可避免地带有误差，个别数据的误差还很大。采用插值公式必须严格通过各个节点，如图2-19中的曲线1，插值后的曲线保留了所有的误差，这是插值公式的主要缺点之一。另外，高阶插值公式求解困难，而分段插值难以保证各段曲线在连接点处的平滑过渡。

鉴于上述情况，工程上常采用数据的曲线拟合方法。拟合曲线不要求严格通过所有节点，而是尽量反映数据的趋势，如图2-19中的曲线2所示。最常用的拟合方法是采用最小二乘法。拟合之前，还可将节点数据（x_i，y_i）（i=1，2，…，n）用图示法表示出来，剔除其中有明显误差的点，以提高拟合精度。

对于一组数据（x_i，y_i）（i=1，2，…，n），可用一个m次多项式拟合（m<n），即

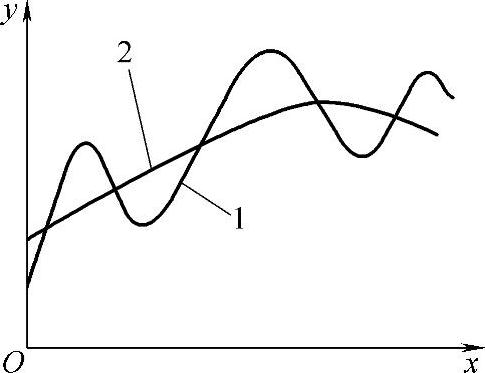
图2-19 数据的曲线拟合

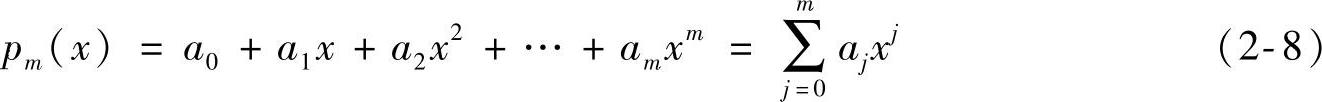
该多项式的第i个节点的函数值与相应数据点之间的偏差为D_i，即

D_i=p_m（x_i）-y_i（2-9）

拟合的基本要求是使各个节点偏差D_i的总和最小。由于偏差有正有负，不能简单地进行求和。最小二乘法要求各个节点偏差D_i的平方和最小，设偏差D_i的平方和为φ，即

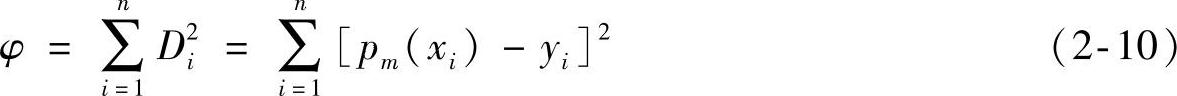(www.xing528.com)

由于节点数据（x_i，y_i）是已知数，因此，将p_m（x）的值代入式（2-10），便成为多项式系数a_i（i=1，2，…，n）的函数，即

使式（2-11）的偏导数，求出φ为极小值时的a₀，a₁，a₂，…，a_m值，便可得多项式p_m（x），它就是偏差平方和极小值的拟合曲线方程式。在通常应用中，取m<n，若m=n，所得的多项式就是拉格朗日插值多项式。

3.线图的程序化

在设计手册中，有些参数之间的函数关系是用线图表示的，包括直线、折线和各种曲线图。线图的特点是鲜明直观，变化趋势明显。但是，线图本身不能直接存储在计算机中，因此在计算机辅助设计时，必须将线图变换成相应的数据形式存储，供设计时检索调用。处理线图时，可先将其转换为数表，然后用前面讲过的数表程序化方法将其程序化；也可以将线图公式化，在设计程序中直接调用。

无论用何种方法处理线图，都必须首先将线图离散化。图2-20所示为15钢实心件正挤压时模具单位面积上挤压力p与变形程度Ψ的关系。为了把此线图变换成数表，可在曲线上取一些节点，把这些点的坐标值列成一张一维数表，见表2-1。

表2-1 15钢实心件正挤压时挤压力与变形程度的关系

图2-20 15钢实心件正挤压时挤压力与变形程度的关系

节点的选取随曲线的形状而异，选取的基本原则是使各节点函数值之间相差不致很大。

由上可知，一条曲线可变换为一张一维数表。上述线图是15钢的变形程度与单位面积上挤压力的关系，对于其他材料也有类似的曲线。于是，可以将各种材料的表组合成一张二维数表，经程序化处理后便可在设计程序中调用。

图2-21所示为凹模、凸模的圆角半径与黄铜极限拉深系数的关系。横坐标为凹模圆角半径r_d和板厚t之比，纵坐标为极限拉深系数。图中的4条曲线分别代表凸模圆角半径r_p和板厚t之比为1、2.5、8、10时的关系，这4条曲线可以用二维数表表示。当用数组结合这个数表时，二维数组的行可表示为r_d/t，列可以表示为r_p/t，数组元素就是极限拉深系数m。

除可将线图程序化外，还可以将其公式化，即用插值方法或最小二乘法将离散化的线图转化为公式。

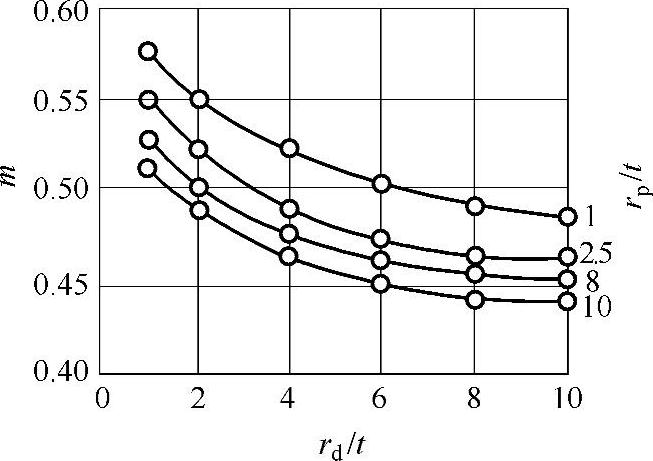
图2-21 黄铜的极限拉深系数与凹模、凸模圆角半径的关系