参数化设计：创新思维为产品带来变革

参数化设计是以一种全新的思维方式进行产品的创建和修改。它用约束来表达产品几何模型，定义一组参数来控制设计结果，从而能通过调整参数来修改设计模型。这样，设计人员在设计时，无需再为保持约束条件而操心，可以真正按照自己的意愿动态地、创造性地进行新产品设计。参数化设计方法与传统方法相比，最大的不同在于它存储了设计的整个过程，设计人员的任何修改都能快速地反映到几何模型上，并且能设计出一组形状相似而不是单一的产品模型。

参数化设计是新一代智能化、集成化CAD系统的核心内容，新的设计系统都增加了参数化设计功能。参数化设计技术以其强有力的草图设计、尺寸驱动修改图形的功能，成为初始设计、产品建模及修改、系列化设计、多种方案比较和动态设计的有效手段。

1.参数化设计

在参数化设计系统中，首先必须建立参数化模型。参数化模型有多种，如几何参数模型、力学参数模型等。这里所提到的为几何参数化模型。

几何模型描述的是几何特征实体，因而适合用图形来表示。几何模型包括两个主要概念：几何关系和拓扑关系。几何关系是指具有几何意义的点、线、面，具有确定的位置（如坐标值）和度量值（如长度、面积）。所有的几何关系构成了几何信息。拓扑关系反映了形体的特征和关系。所有的拓扑关系构成其拓扑信息，它反映了物体几何元素之间的邻接关系。

在计算机辅助设计系统的设计中，不同型号的产品往往只是尺寸不同而结构相同，映射到几何模型中，就是几何信息不同而拓扑信息相同。因此，参数化模型要体现零件的拓扑结构，从而保证设计过程中几何拓扑关系的一致性，实际上，用户输入的草图中就隐含了拓扑元素间的关系。

几何信息的修改需要根据用户输入的约束参数来确定，因此，需要在参数化模型中建立几何信息和参数的对应机制，该机制是通过尺寸标注线来实现的。尺寸标注线可以看成一个有向线段，上面标注的内容就是参数名，其方向反映了几何数据的变动趋势，长短反映了参数值，这样就建立了几何实体和参数间的联系。由用户输入参数（或间接计算得到的参数）的参数名找到对应的实体，进而根据参数值对该实体进行修改，实现参数化设计。

产品的参数化模型是带有参数名的草图，由用户输入。图2-16a所示为一图形的参数化模型，所定义的各部分尺寸为参数变量名。

对于拓扑关系改变的产品零件，也可以用它的尺寸参数变量来建立参数化模型。如图2-16b所示，其中，N为小矩形单元数，T为厚度，A、B为单元尺寸，L、H为长和宽。但是，单元数量的变化会引起尺寸的变化，它们之间必须满足条件

L=NA+（N+1）T

H=B+2T

这个条件关系称为约束。约束可以理解为若干个对象之间所希望的关系，也就是限制一个或多个对象满足一定的关系，对约束的求解就是找出约束为真的对象的值。

由于所有的几何元素都能根据其几何特征和参数化定义相联系，从而所有的几何约束都能看成代数约束。因此通常情况下，所有的约束问题都可以从几何元素级归纳到代数的约束级，实际上参数化设计的过程可以认为是改变参数值后对约束进行求解的过程。

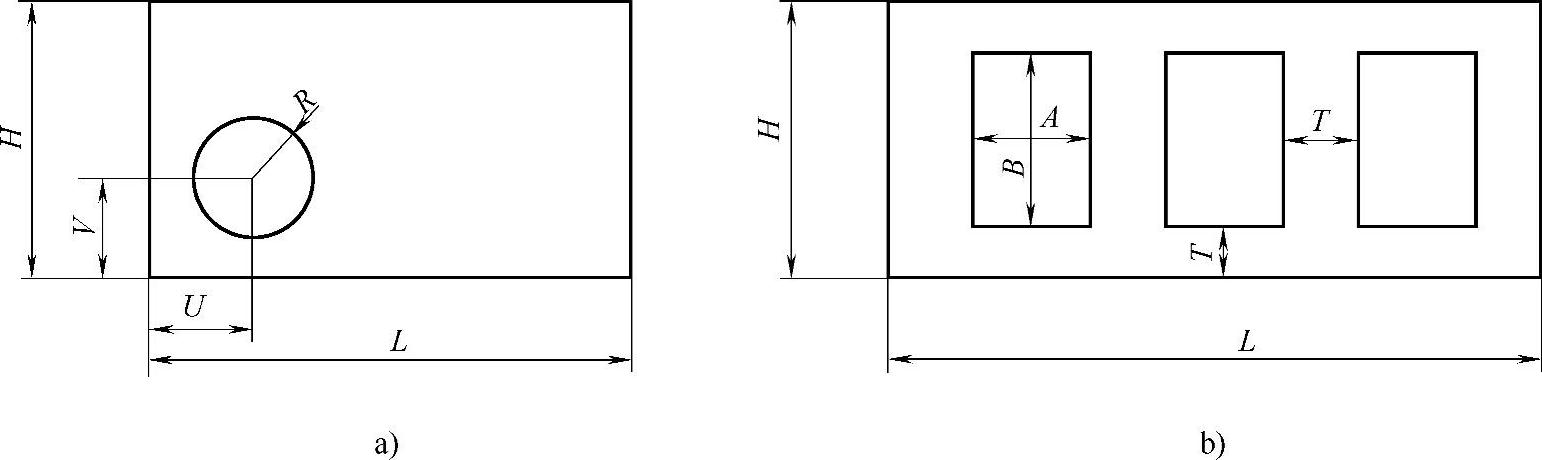
图2-16 参数化模型

2.参数化设计的功能

参数化设计的功能主要有：

1）从几何参数化模型自动导出精确的模型。它不要求输入精确图形，只需输入一个草图，标注一些几何元素的约束，然后改变约束条件来自动地导出精确的几何模型。

2）通过修改局部参数来达到自动修改几何模型的目的。这对于大致形状相似的一系列零件，只需修改一下参数便可产生新的零件，从而大大提高了零件生成的效率。

3.参数化设计的主要方法

参数化设计的方法在理论上研究比较早。在20世纪80年代初，研制Build系统的Hill-yard和Cossard进行了大量研究，进而完善了变动几何法和几何推理法。

（1）变动几何法（Variational Geometry）该方法的思想是将一系列约束转化成一系列关于特征点的非线性的方程组

F（D，X）=0

然后再用数值求解法求解此方程。其中F：（f₁，f₂，…，f_n）是一系列函数；D：（d₁，d₂，…，d_n）是F函数的变量，表示尺寸的约束；X：（x₁，x₂，…，x_n）是F函数的变量，它表示最后获取的几何特征点的坐标，包括结果值。(www.xing528.com)

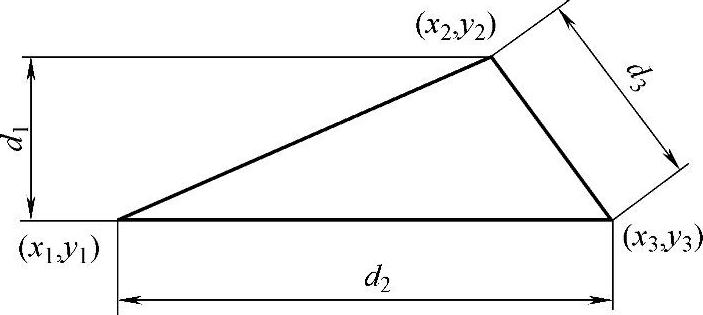
图2-17 二维参数化设计

例如，一个二维的简单三角形，假定d₂是水平线，且图形原点取在（x₁，y₁）处，如图2-17所示，按传统设计方法，不需标注图上所示尺寸，仅用画线、点功能绘制出来即可。而利用交互方式标注的尺寸，与图形的模型无关，仅显示给设计者看而已。而参数化设计则需把约束关系建入模型中，与数据模型形成一个整体。这样给出的仅仅是一个草图，不过其拓扑结构应保持不变。需要绘图时，即需要确定这个几何模型时，要求把这三个点（x₁、y₁）、（x₂，y₂）、（x₃，y₃）的实际的精确几何坐标求出，就可以得到精确的几何图形。其关键是如何求出这三个点。这些点在变动几何法中称为特征点。

对于上述三角形，在变动几何法中，其做法是在整体上列出一个方程组，即

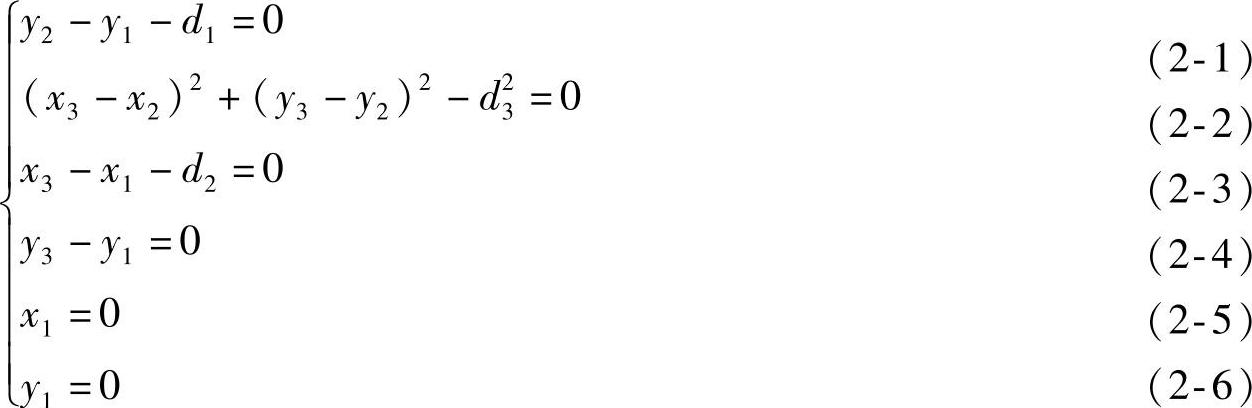
对于x₁、x₂、x₃、y1、y2、y3这6个未知数需要6个方程组联立求解。很明显其约束只有3个（即d₁、d₂、d₃），故可列出式（2-1）、式（2-2）和式（2-3）。由于d₂已确定为水平线，故可以视为这是一个水平约束，它是一个隐含约束，故可列出式（2-4）；而（x₁，y₁）已假定为坐标原点，则有式（2-5）和式（2-6）。因此得出了6个方程组，通过解方程求得精确的x₁、y₁、x₂、y₂、x₃、y3。

当修改时，若d₁拉长，则系统就自动地把（x₂，y₂）定到了一个新的位置。这样，把约束和几何信息联系起来，成为一个大的方程组，可见变动几何法是属于整体求解方法。

（2）几何推理法20世纪80年代中后期，随着人工智能的发展，人们研制了另一种新方法——几何推理法（GeometricReasoning），它是将人工智能的技术运用到实体造型系统中构成的。

几何推理法的原理是指从已知元素和几何约束，通过推理逐步确定出未知元素。它与几何变动法相比，仅属于一种局部求解的方法。它采用人工智能语言（LISP、Prolog等）编程。

几何推理法本身又分为两种，即基于推理机方法和基于普通程序设计方法。

基于推理机的方法是人工智能方法，其系统结构包括两个部分，即推理部分和几何计算部分，如图2-18所示。

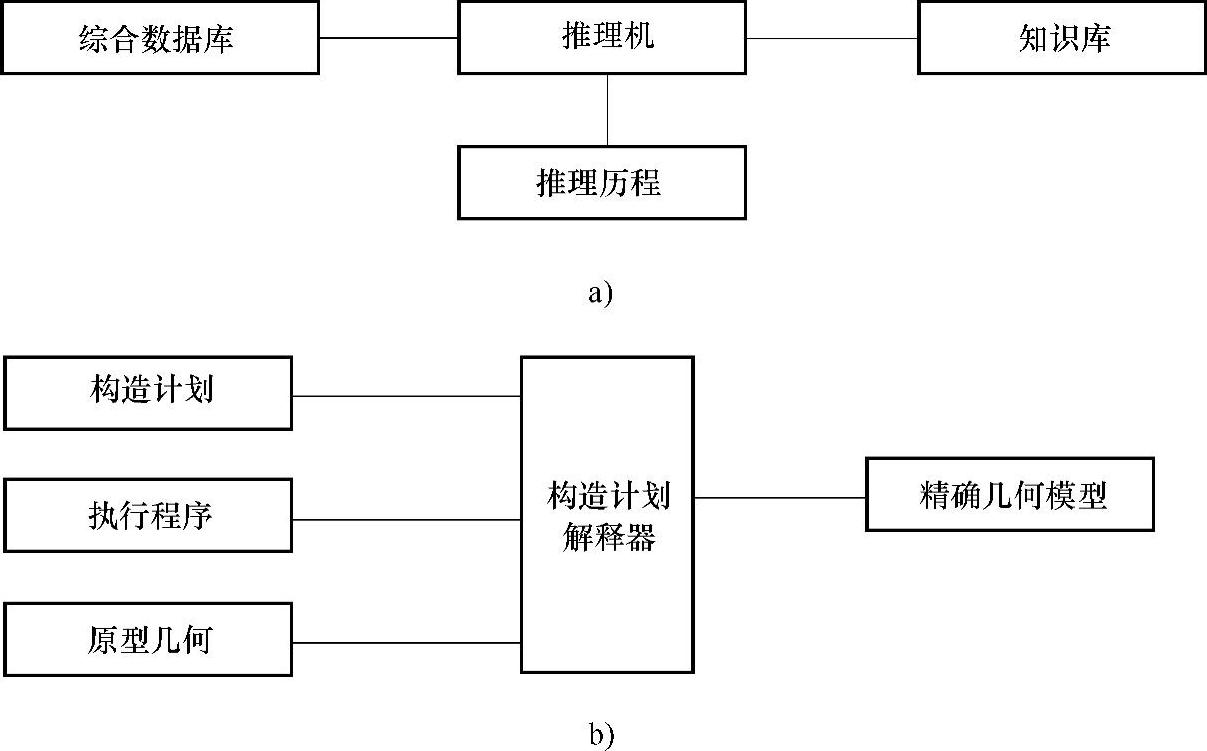
图2-18 基于推理机法的系统结构图

a）推理部分 b）几何计算部分

1）推理部分。推理部分的系统结构框图如图2-18a所示。知识库用于存放领域的专门知识。专门知识含有同领域问题相关的理论知识、常识性知识，也含有专家凭经验得到的启发式知识及领域内有关的定义、定理、确定的及不确定的运算（推理）法规等。例如，已知圆弧的两个端点和圆心，就可以计算出该圆弧。可以将它的计算方程通过知识获取机制接纳到知识库，构成一条推理规则。

综合数据库存放与问题有关的初始数据及系统求解期间产生的所有中间结果。它反映了当前状态下欲求解的问题的描述。例如特定的几何约束（尺寸、线段、隐含约束等外部信息）经用户界面输入并转换成系统的内部表示形成后，作为初始问题描述存入综合数据库中。

推理机以一定的控制策略，针对综合数据库中的当前问题，搜索知识库中对当前问题有用的知识进行推理。在没有达到最终结果之前，更新当前问题的描述，做进一步的搜索、推理，直到获得最终的求解结果。

推理历程模块记录下整个推理的过程和最终得到的结果——几何元素，然后由几何计算部分调用结果数据。

2）几何计算。几何计算部分常用高级语言（如C、FORTRAN等）编程实现，若用LISP等人工智能语言编程，则效率会很低。

几何计算部分的系统结构框图如图2-18b所示，它包括构造计划及其解释器、执行程序、原型几何、精确几何模型等部分。

在推理部分中，推理历程模块记录的推进过程，就是一个构造计划，由构造计划模块取出后，将其内容送到构造计划解释器去进行解释。因为此构造计划是一系列字符串，故需要构造计划解释器解释后才可以辨别出哪些是变量，需用哪些函数来计算，然后调用执行程序模块中的执行程序来执行，以得出精确几何模型。几何计算部分中的原型几何模块的功能用来克服多解的问题，因为有时一个方程可能有多个解。例如已知距离，而它的端点应根据草图所指定的大致位置而定，也就是原型几何模块中存放了初始设计时的草图，从而避免了多解。所以整个几何计算过程为：从构造计划出发，经过构造计划解释器的解释，调用执行程序加以执行后，通过原型几何进行选择，最后得出精确的几何模型。

由此可见，几何推理的思想是：根据初始条件和提供的约束，经过推理，它可知道用哪些约束可以解出哪些“知识”，根据这些“知识”又可解出另一些解，从而把可解的“知识”全解出来，直到获得最后解。显然几何推理是局部求解的，是一步步推导出来的。它的推导部分是一个专家系统，采用LISP等人工智能语言编程。