图形变换是计算机图形学的基本内容之一。通过图形变换可以将简单图形变换为复杂的图形,可以将三维物体用二维图形表示。图形变换包括几何变换和非几何变换,几何变换是指改变图形的几何形状和位置,而非几何变换则是改变图形的颜色、线型等非几何属性。这里主要介绍图形的平移、比例和旋转等基本几何变换。
1.二维图形变换
(1)变换原理
1)平移变换。xOy平面上的点P(x,y)在其坐标方向上增加平移量Tx和Ty,可变换至新位置(x′,y′)。平移变换的关系式为
x′=x+Txy′=y+Ty
平移使图形相对于原坐标系由一个位置移动至另一个位置,而图形本身不发生变化。
2)比例变换。若点的x、y坐标分别乘以Sx和Sy,可得到新的点,如图2-4所示。这种变换称为比例变换,Sx和Sy为两坐标方向上的比例系数。比例变换的关系式为
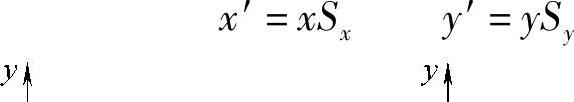
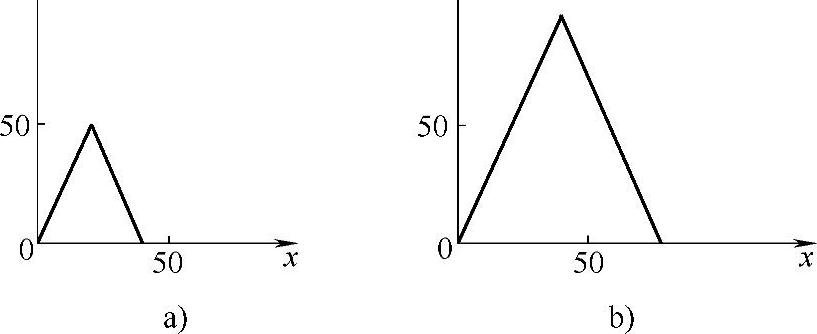
图2-4 图形的比例变换
a)原来的点 b)新的点
比例变换有多种用途,当Sx=Sy时,可把图形放大或缩小;当Sx≠Sy时,产生的效果相当于把图形沿平行于坐标轴的方向拉延或压缩,使图形发生变形,如图2-5所示;当Sx或Sy为负值时,变换后的图形与变换前的图形相对于x轴或y轴对称,即可产生图形的镜像。
如图2-6所示为当Sx=-1,Sy=1时产生对y轴的镜像。当Sx=Sy=-1时,镜像对称于坐标系原点。通过变换产生原图形镜像的变换又称为反射变换。
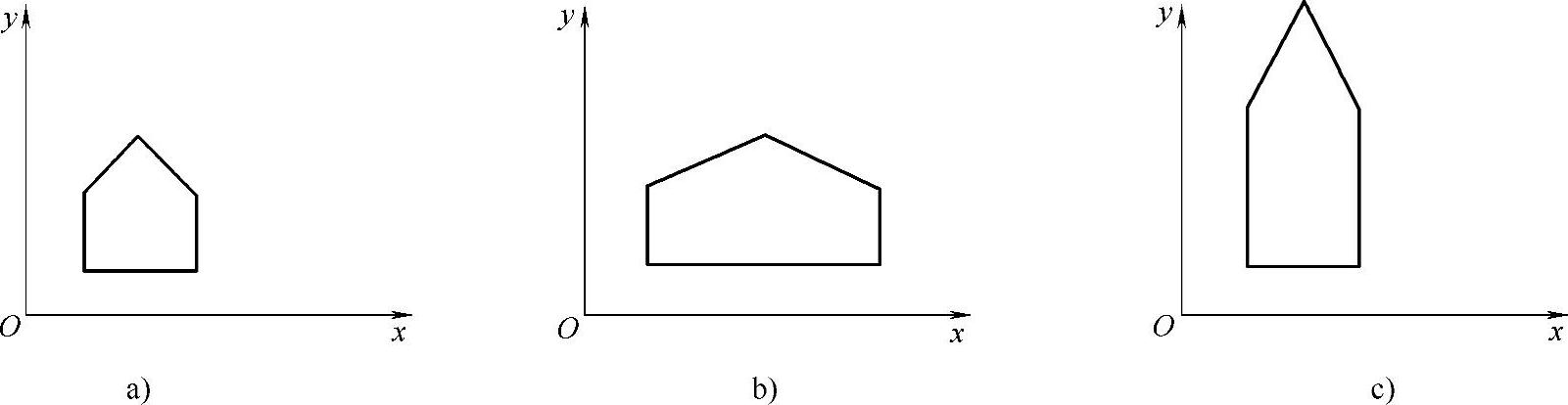
图2-5 利用比例转换使图形发生变形
a)变换前 b)沿x轴方向拉延 c)沿y轴方向拉延
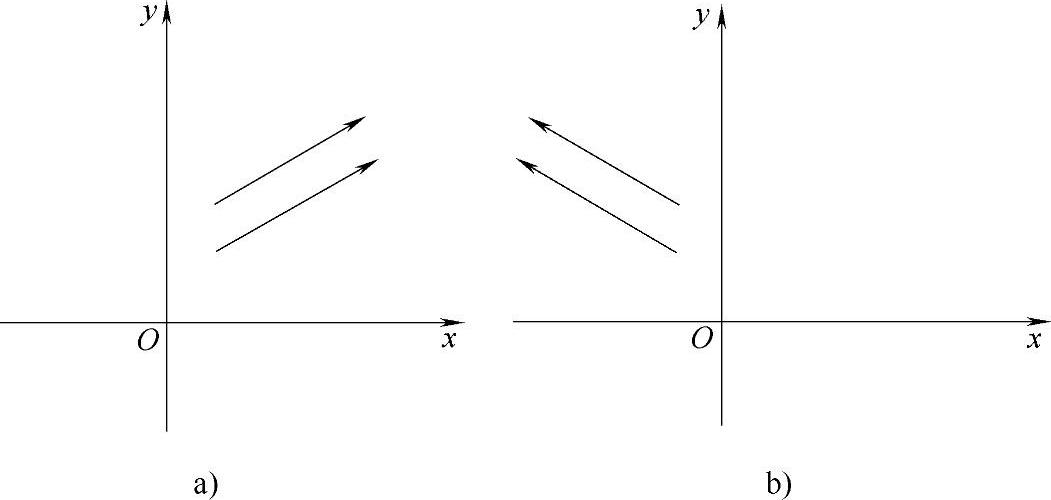
图2-6 利用比例变换产生对称图形
a)变换前 b)对y轴的反射变换
3)旋转变换。图形绕坐标原点旋转某一角度生成变换后的图形,这种变换称为旋转变换。
设点P(x,y)绕原点O顺时针方向旋转θ角后达到P′(x′,y′),则
x′=xcosθ+ysinθy′=-xsinθ+ycosθ
图2-7所示为三角形绕坐标原点顺时针旋转45°的变换情况。三角形的顶点坐标分别由原来的(20,0)、(60,0)、(40,100)变为(14.14,-14.14)、(42.43,-42.43)、(98.99,42.43)。
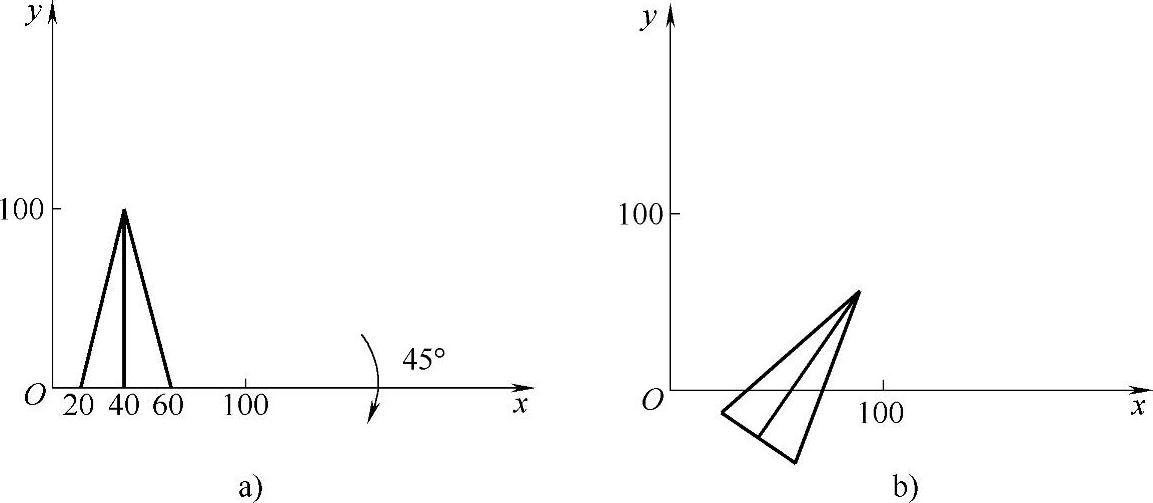
图2-7 图形的旋转变换
a)变换前 b)变换后
(2)变换的矩阵表示
1)齐次坐标。对点向量[xy]和[x′y′]引入第三分量,使它们成为[xy 1]和[x′y′1]。位置向量[xy 1]和[x′y′1]中的第三元素1,可看做一个附加坐标,即平面上的一个点(二维向量)用3个坐标(三维向量)来表示。这种用三维向量表示二维向量,或用n+1维向量表示n维向量的方法称为齐次坐标表示法。在齐次坐标表示法中,n维向量的变换是在n+1维空间内实现的。在n+1维齐次空间中的一个向量可看做一个n维空间中的向量多了一个比例因子H。通常笛卡儿坐标系中的二维点[xy]的齐次表达式是[HxHyH],其中H≠0。于是,给出点的齐次表达式[XYH],就可以得到二维笛卡儿坐标,即
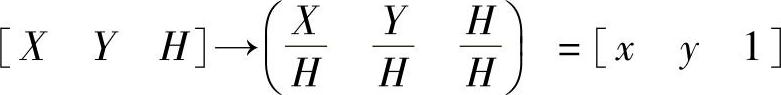
这个过程称为正常化处理。
用齐次坐标时不存在位置向量的唯一表示。例如,齐次坐标[15 9 3],[-30-18 -6]和[5 3 1]都表示笛卡儿坐标点(5,3)。在二维变换中,为简单起见,令H=1。此时二维坐标点(x,y)的齐次坐标表示为[xy 1],其中x、y坐标没有变化,只是增加了H=1的一个附加坐标。在几何意义上,相当于把发生在三维空间的变换限制在H=1的平面内。
2)变换矩阵。如果点的位置向量用齐次坐标表示,那么平移变换矩阵、比例变换矩阵和旋转变换矩阵将分别采用如下形式。
平移变换矩阵

比例变换矩阵
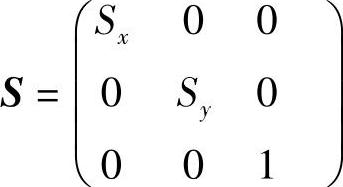
旋转变换矩阵
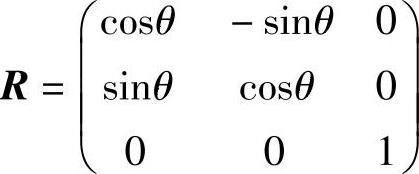
若对点[xy 1]进行平移变换,则有
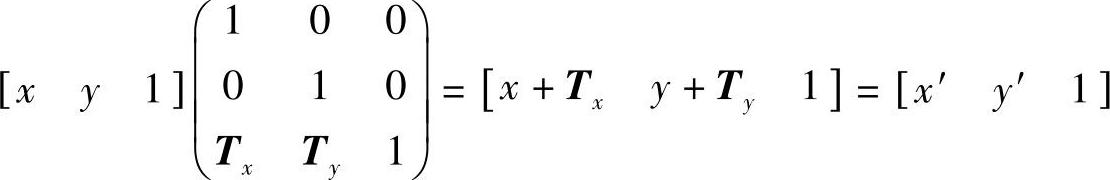
当S>1时,对点的位置向量进行如下变换,可使两个坐标同时缩小。即
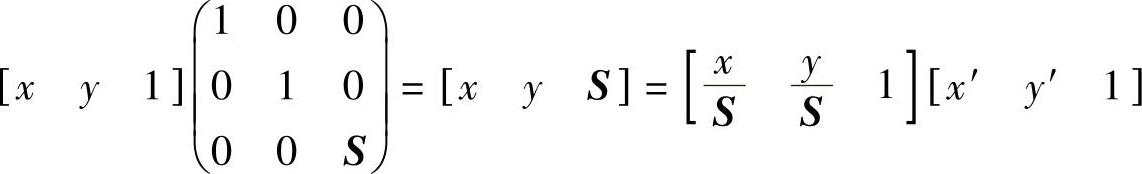
以上3种变换都具有可逆性,即
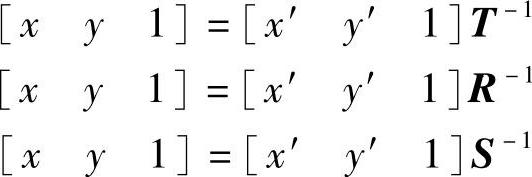
(3)变换的级联 图形除了需要进行以上所讨论的一些简单变换外,还需要进行更复杂的变换。例如,图形绕任意点旋转,可以通过3个简单变换来实现,即平移→旋转→平移。一系列的简单变换(变换顺序)可以通过级联组合成一个变换。
在对变换序列进行级联时,顺序问题十分重要。例如,将图2-8a所示三角形旋转90°,然后平移Tx=-80,Ty=0,变换后的情形如图2-8b所示。若将变换次序颠倒,则得到的图形如图2-8c所示。
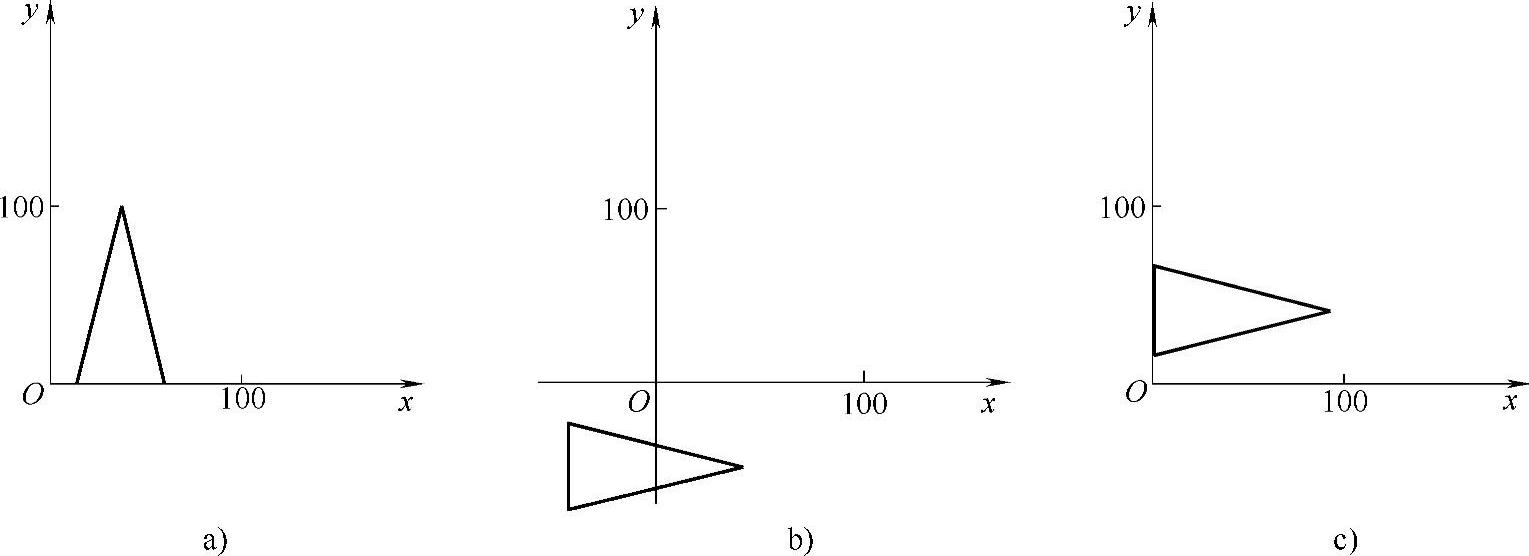
图2-8 不同变换顺序产生的结果
a)变换前 b)旋转—平移 c)平移—旋转
级联的目的是将一个变换顺序表示成一个变换。假设点P经过n次变换T1,T2,T3,…,Tn,则总的变换结果为
P′=PT1T2…Tn-1Tn=PT
所以,总的变换矩阵
T=T1T2…Tn-1Tn
例 求绕平面上任意点旋转的变换矩阵,如图2-9所示。
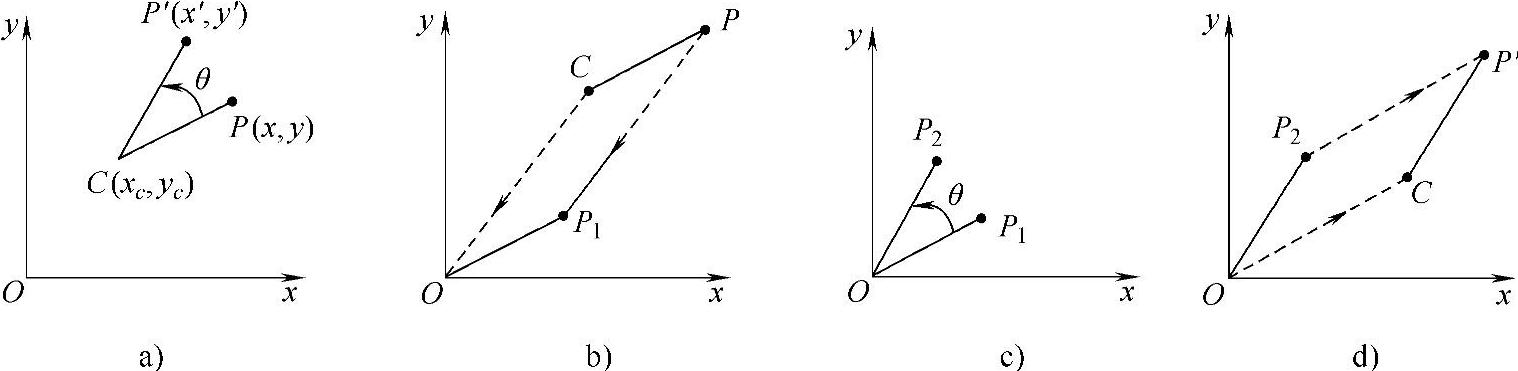
图2-9 绕平面上任意点的旋转变换
a)绕O点旋转θ角 b)平移 c)旋转 d)平移
绕平面上任意点C(xc,yc)的旋转是一个组合变换。可以通过下列步骤实现:首先将旋转中心平移到坐标原点;然后进行旋转变换;最后再平移变换,恢复原坐标系。通过以上3种变换的有序级联,可求得其组合结果,即总的变换矩阵为
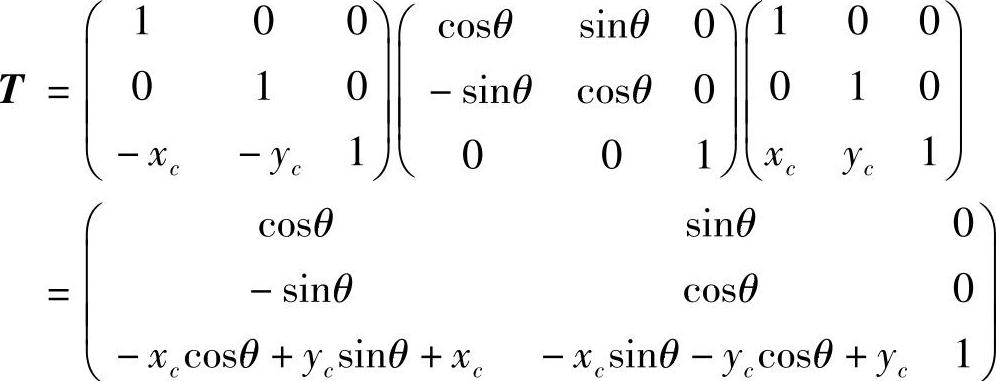
2.三维图形变换
前面所讨论的二维变换扩展到三维时,三维点的位置向量齐次坐标表示为[xyz 1],齐次变换矩阵是4×4方阵,即
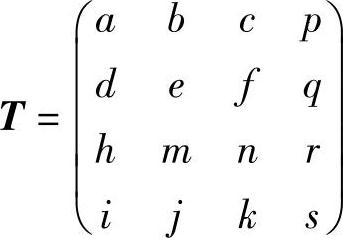 (https://www.xing528.com)
(https://www.xing528.com)
因此,三维空间点的变换可写为
[XYZH]=[xyz 1]T
正常化处理后的坐标为
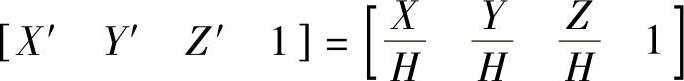
下面介绍一些基本的三维变换。
(1)平移变换 把点(x,y,z)平移到新点(X,Y,Z)的变换为
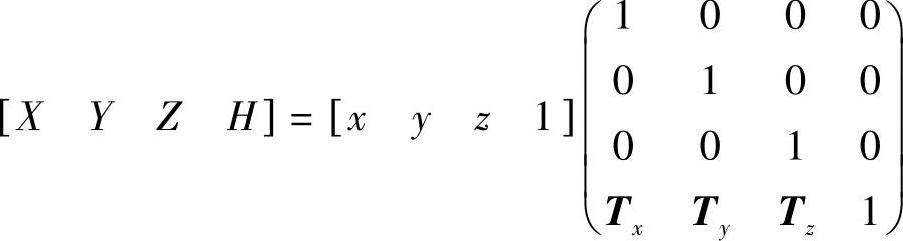
式中,Tx、Ty、Tz分别为在x、y、z坐标轴方向上的平移分量。
(2)比例变换 用比例变换可以分别调节每个坐标方向上的大小。
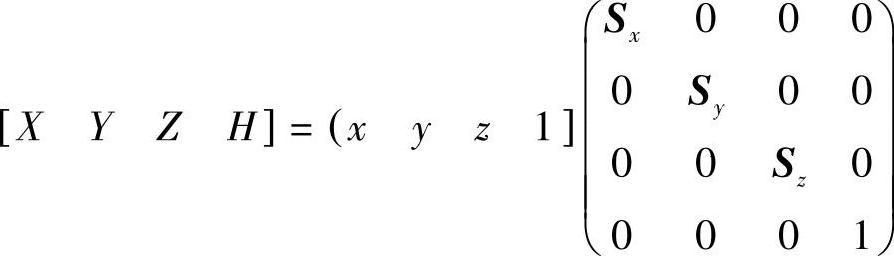
均匀缩放图形大小的变换为
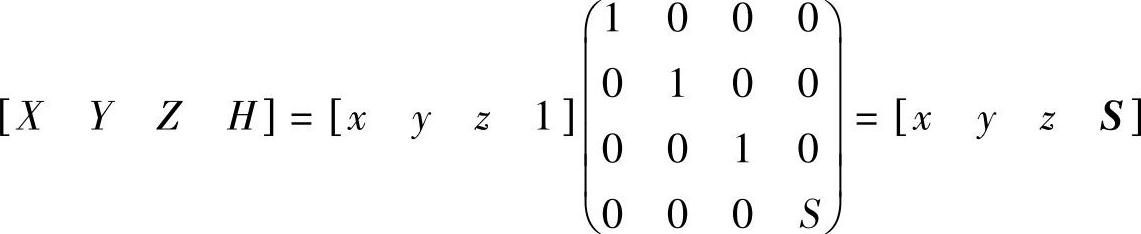
正常化处理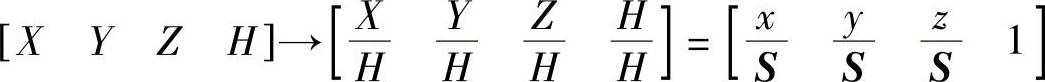
若S>1,则整个图形缩小;若S<1,则整个图形放大。
(3)旋转变换
1)绕坐标轴旋转变换矩阵。绕z轴旋转角θz角,如图2-10a所示,变换矩阵Rz为
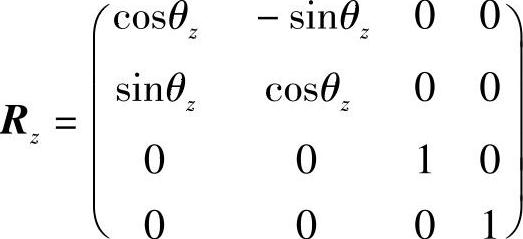
绕y轴旋转θy角,如图2-10c所示,变换矩阵Ry为
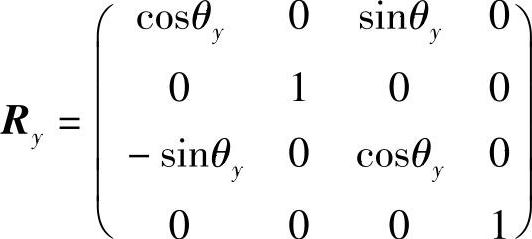
绕x轴旋转θx角,如图2-10b所示,变换矩阵Rx为
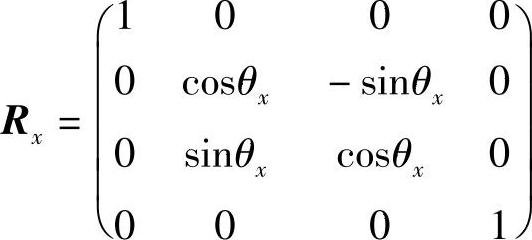
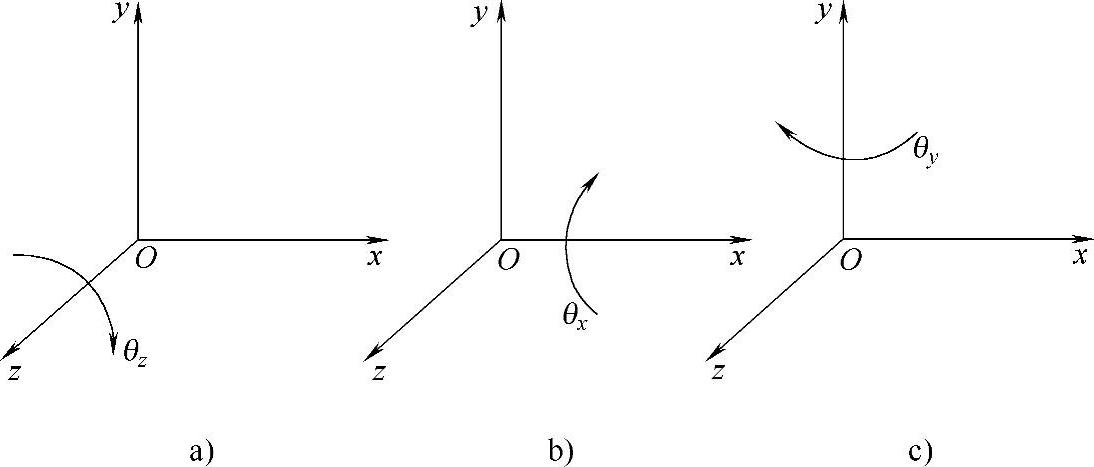
图2-10 绕3个坐标轴的旋转
2)绕空间任意轴的旋转变换。图形绕空间任意轴(不通过坐标原点)的旋转,可以用组合变换实现。首先把坐标原点移到旋转轴上;然后绕x和y轴旋转,使旋转轴与z轴重合,这样图形绕任意轴旋转θ角就转化为绕轴z旋转θ角;最后,绕y轴和x轴作相反方向的旋转及平移,恢复原坐标系,如图2-11所示。
用直线上的一点和该直线的方向来定义空间任意轴,这样,点的位置向量可提供平移信息,而直线的方向可提供使它旋转到与z轴重合的正确角度。设给定直线的参数方程为
x=Aμ+x1y=Bμ+y1z=Cμ+z1
在直线上的一点是(x1,y1,z1),直线的方向由[ABC]向量定义。其变换序列如下:
①移动原点到旋转轴上的平移变换矩阵为
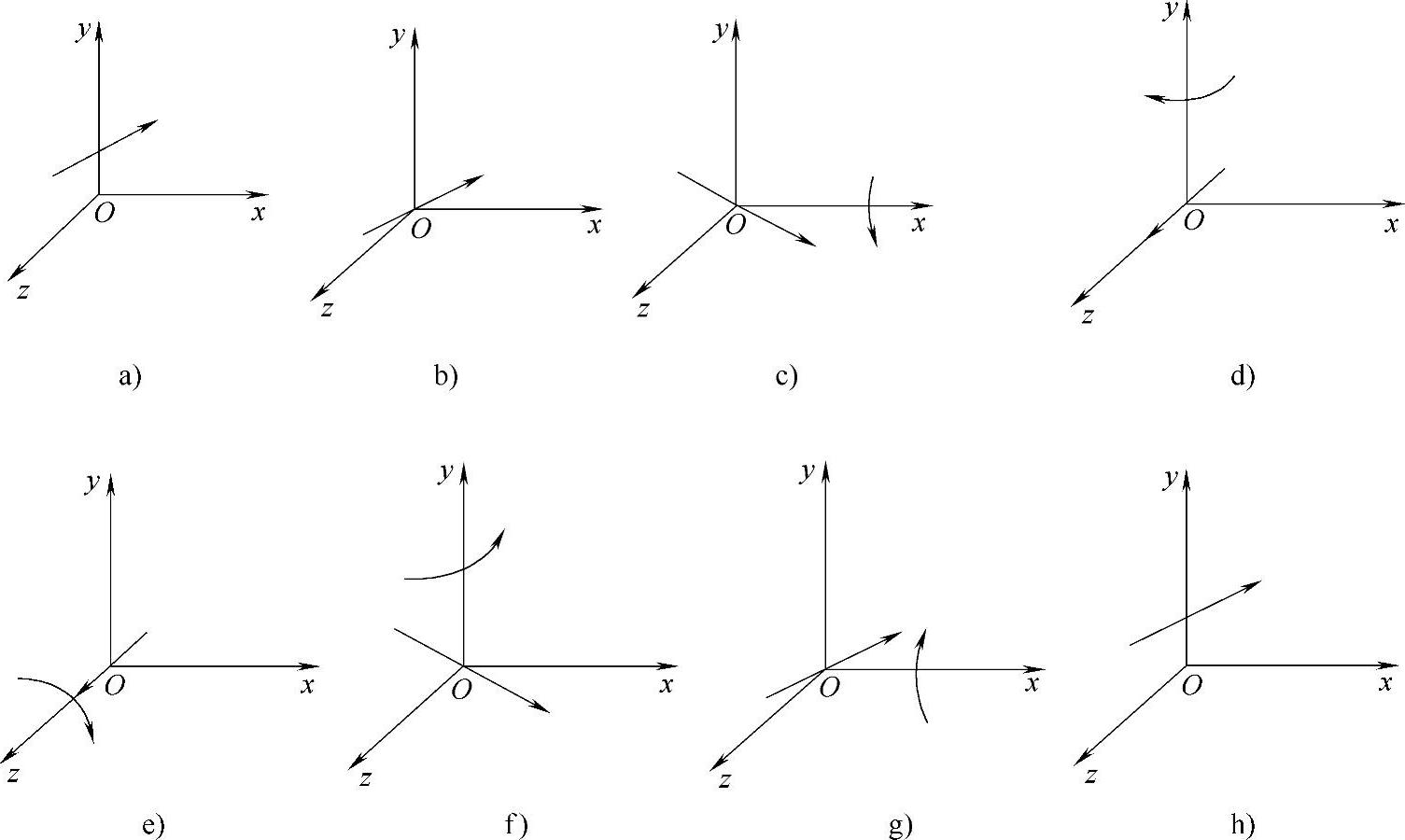
图2-11 绕空间任意轴的旋转变换
a)原状 b)平移至原点 c)绕x轴旋转至Oxy平面 d)绕y轴旋转,使旋转轴与z轴重合 e)绕z轴旋转返回 f)绕y轴旋转返回 g)绕x轴旋转返回 h)平移返回
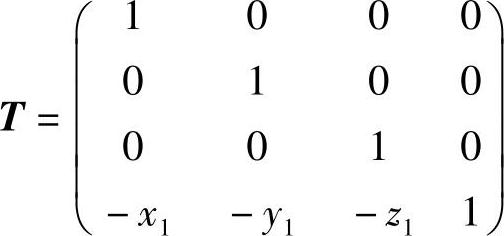
②绕x轴旋转直到旋转轴位于Oxz平面内。为了确定所需的旋转角度,把直线的方向向量置于新坐标系的原点上,如图2-12所示,研究它在Oyz平面上的投影。因平移的结果使原点(0,0,0)处于旋转轴上,所以在(0,0,0)和(A,B,C)之间的线段L必须在旋转轴上。L在Oyz坐标面上的投影是从(0,0,0)到(0,B,C)之间的线段l′。
若绕x轴旋转直到旋转轴在Oxz坐标面内,则l′将与z轴重合。使l′与z轴重合,需逆时针旋转I角。因为
l′=(B2+C2)1/2
sinI=B/l′
cosI=C/l′
因此绕x轴旋转变换矩阵应为
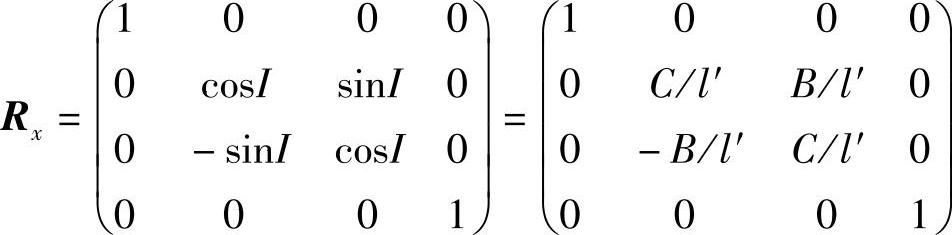
因为绕x轴旋转时,x坐标不变;线段长度L不变,L=(A2+B2+C2)1/2;z坐标为
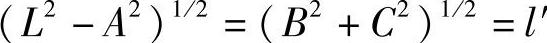
所以经Rx变换后,就可画出位于Oxz坐标面内的旋转轴,如图2-13所示。
③绕y轴顺时针旋转J角,使旋转轴与z轴重合,因为
sin J=A/L cos J=l′/L
所以绕y轴旋转变换矩阵为
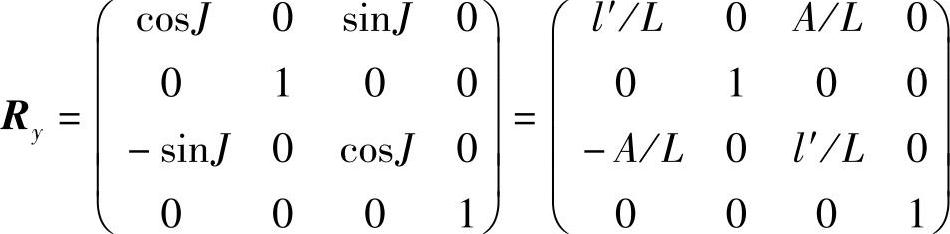
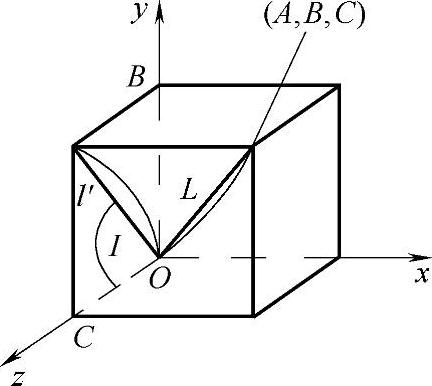
图2-12 绕x轴转角的确定
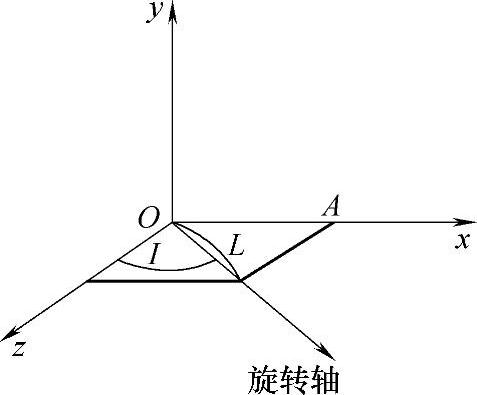
图2-13 位于Oxz平面内的旋转轴
④绕z轴旋转θ角,变换矩阵为
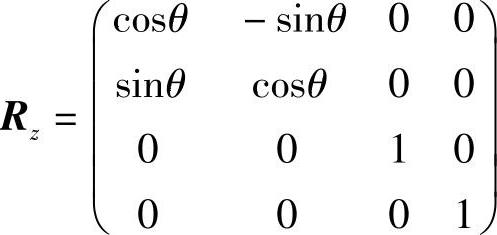
然后进行恢复原坐标系的变换。
⑤绕y轴逆时针旋转J角,变换矩阵为
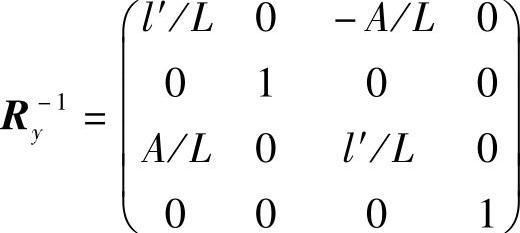
⑥绕z轴顺时针旋转I角,变换矩阵为
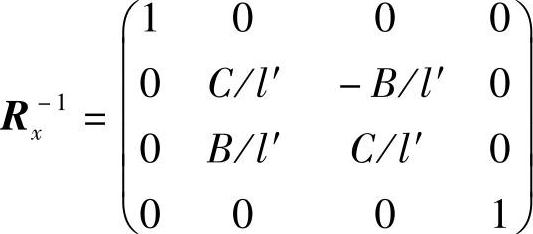
⑦平移使坐标原点返回到它原来的位置,变换矩阵为
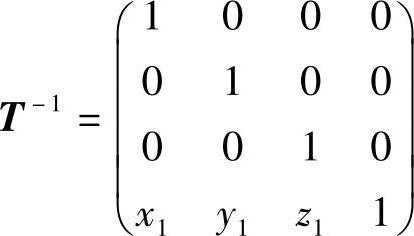
绕任意轴旋转θ角的变换矩阵Rθ是以上给出的变换矩阵之乘积,即
Rθ=TRxRyRzRy-1Rx-1T-1
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




