滚动轴承故障诊断模型：基于PELCD、LS和VPMCD

本节提出的滚动轴承故障诊断模型，包含如下四个步骤：

（1）首先采用PELCD对滚动轴承每个原始振动信号进行分解，得到若干个ISC分量；

（2）选择前三个ISC分量，提取它们的时域和频域特征值以及振动信号的时频熵，由此组成初始特征向量，即：提取前三个分量I1（t）、I2（t）和I3（t）的特征参数：KS，SF，IF，FE，FG，FSTD，FRMS，再提取振动信号的时频熵TFE。于是可构建特征向量：T=（TFE，KS1，SF1，IF1，KS2，SF2，IF2，KS3，SF3，IF3，FE1，FE2，FE3，FG1，FSTD1，FRMS1，FG2，FSTD2，FRMS2，FG3，FSTD3，FRMS3）。T的维数为1×22，为方便，T的各对应特征值记为Ti，i=1，2，…，22。

（3）计算由初始特征向量T组成的初始特征向量矩阵的LS分值，依据分值由低到高对特征量进行排序，选择分值较小的前若干个特征向量作为最优特征向量。

（4）将最优特征向量输入VPMCD分类器进行训练和测试，实现滚动轴承故障诊断。

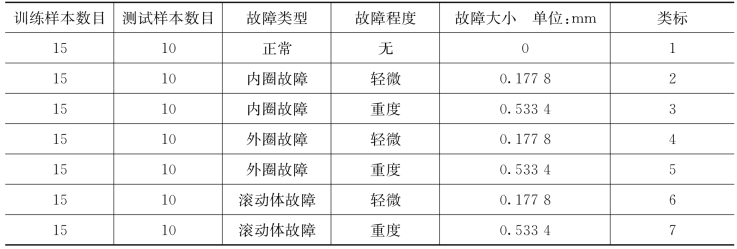
为了验证本节提出的滚动轴承故障诊断模型的有效性，采用滚动轴承试验数据对其进行验证。试验数据来自美国凯斯西储大学滚动轴承数据中心，试验数据说明如表7.3所示，各类信号的时域波形如图7.10所示。

上述试验数据中，故障类型分为外圈故障、内圈故障和滚动体故障，每种故障程度可分为轻微故障和重度故障，加上正常状态，共七种状态类别，每一类取15个样本作为训练，10个样本作为测试，共得到105个训练样本，70个测试样本。

表7.3　试验数据类别描述

首先，采用PELCD分别对每一类的每个振动信号进行分解，得到若干个ISC分量。

其次，提取前三个分量I1（t），I2（t）和I3（t）的上述特征参数和振动信号的时频熵，构建特征向量T，T=（Ti）1×22。

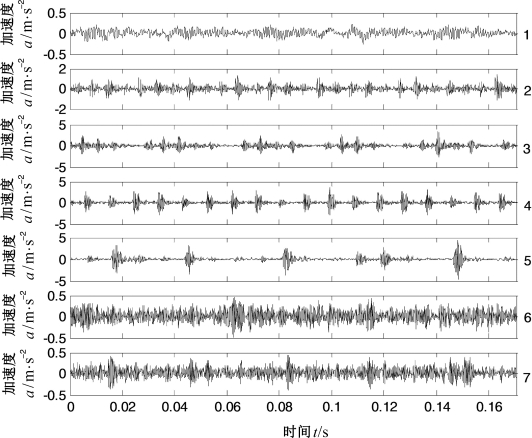
图7.10　正常和故障轴承振动信号的时域波形（图形右端数字对应表7.3中类标）

第三，将105个训练样本的特征向量T组成初始特征向量矩阵C（维数为105×22）。计算矩阵C各特征向量的LS，将22个特征向量按照LS从小到大进行排序，选择分值较小的前五个特征值作为最优特征量（最优特征量个数用J表示）形成最优特征向量矩阵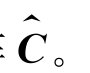

对于上述试验数据，LS由低到高的顺序为：

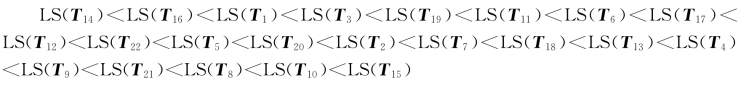
即前五个最优特征值依次为：第一个分量I1（t）的重心频率，第一个分量I1（t）均方根频率，原始信号的时频熵，第一个分量I1（t）的波形指标，第二个分量I2（t）的均方根频率。这说明分解得到的第一个分量I1（t）包含了重要的故障信息，这与文献[244]的结果是一致的。(www.xing528.com)

最后，将最优特征向量矩阵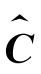（维数105×5）输入VPMCD分类器进行训练，得到各个类别的变量预测模型。依据特征矩阵提取70个测试样本的五个最优特征值（为了与下文比较，仍提取了每个振动信号的22个特征值），得到训练样本70×5的特征矩阵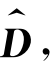，将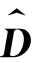输入已训练的VPMCD分类器。测试样本的VPMCD输出结果、训练用时及测试样本的识别率如表7.4所示。由表7.4可以看出，本节提出的方法有很好的分类效果，不仅实现了故障类别的区分，而且也实现了故障程度不同的区分，测试样本的故障识别率较高（100%）。

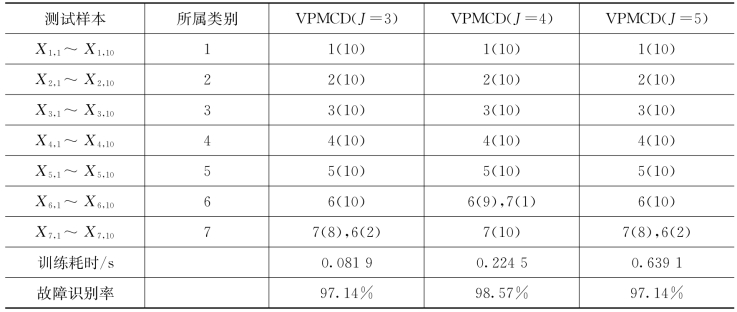
显然，特征向量的维数对诊断结果有重要的影响，若特征向量的维数过小，即特征值个数较少，则无法完全反映和区分故障类型和故障程度，诊断效率不高；若特征值个数较多，则会造成信息的冗余，训练耗时，降低诊断效率。为了比较，本节选择经过LS排序后前J个特征值（J=3，4，5，6，7）作为特征向量输入VPMCD分类器，训练样本和测试样本个数不变，经过训练建立预测模型，测试样本的输出结果、训练耗时及测试样本的识别率如表7.4所示。从表7.4中可以看出特征向量个数对故障诊断结果的影响，特征向量个数过多或过少都不宜。同时表7.4的结论也验证了本节提出的故障诊断模型中选择前五个特征量是可行且合理的。

为了说明LS优化特征向量的必要性及优越性，本节选择未经过LS排序的前J个特征量（J=3，4，5）作为特征向量输入VPMCD分类器，训练样本和测试样本个数不变，经过训练建立预测模型，测试样本的输出结果、训练用时及测试样本的识别率如表7.5所示。对比表7.4和表7.5易发现，由于特征向量未经过LS优化，对相同的VPMCD分类器，分别选择前四个和前五个特征值作为特征向量进行训练，测试样本的识别率明显要比经过LS优化后的特征向量作为输入特征向量的测试样本的识别率要低，这说明LS对特征值进行排序优化具有一定的优越性和必要性。

表7.4　优化特征向量不同时测试样本的VPMCD输出结果

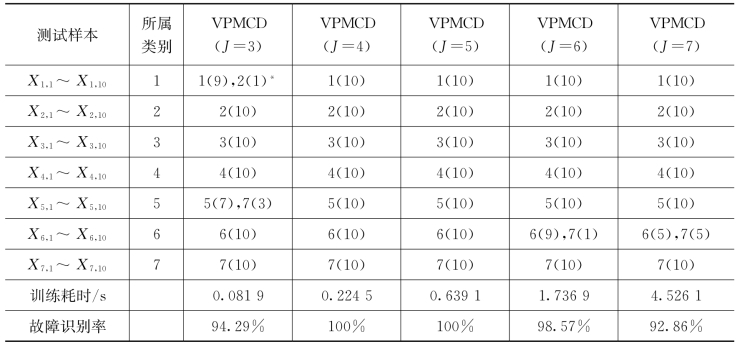
*表示10个测试样本，9个输出为1类，1个错分为2类，其他意义同。

表7.5　特征量未LS优化时测试样本的VPMCD输出结果

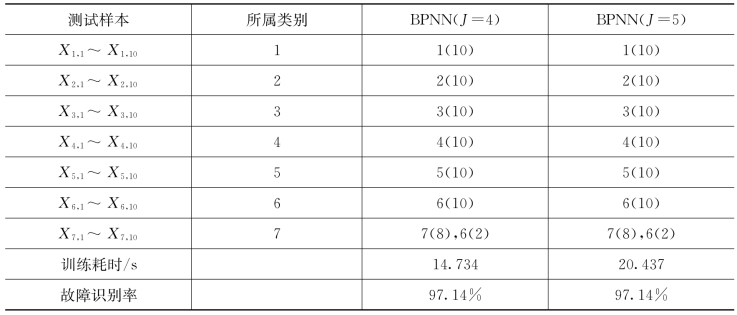
此外，为了说明VPMCD分类器的优越性，采用常用的BP神经网络（BP nerve network，BPNN）分类器重复同样的分类过程，其中网络结构的隐含层20层，输出层7层，训练目标为0.001，最大训练次数为6 000，其他参数为默认设置。特征向量分别由LS优化后的前四个和前五个特征值组成，训练样本和测试样本个数不变，通过训练BPNN分类器，测试样本的输出结果、训练用时及测试样本的识别率如表7.6所示。表7.6和表7.4对比易发现，对于相同的特征向量，BPNN的识别率要低于VPMCD，且耗时较多，这说明VPMCD在耗时方面要优于BPNN，是一种有效的故障分类方法。

表7.6　LS优化的特征量训练的BP神经网络的测试样本输出结果

本节提出的一种基于PELCD，LS和VPMCD的滚动轴承故障诊断模型，该模型具有以下特点：

（1）PELCD克服了LCD分解的模态混叠问题，并对原PELCD方法中的参数进行了优化，使得PELCD对振动信号的分解结果更为精确，是一种有效的数据分析方法；

（2）同时提取振动信号时域、频域和时频域特征值，多角度反映故障特征；

（3）针对提取特征值维数较多，容易造成信息冗余和维数灾难的问题，采用拉普拉斯分值特征选择降低特征向量维数，依据分值选择与故障关系最为密切的特征值，有效地降低了诊断时间，提高了诊断效率；

（4）VPMCD通过对特征值间的内在关系进行预测，无需事先选择参数，自适应地选择最优预测模型实现模式的分类。试验数据表明，与BP神经网络相比，VPMCD在精确性和节约训练时间方面有一定的优越性。