部分集成局部特征尺度分解方法优化

7.4.1.1　PELCD算法

对于一个复杂信号S（t），PELCD的分解步骤简述如下：

（1）假设待分解信号为S（t），添加符号相反的白噪声到S（t），即

其中，ni（t）表示添加的白噪声，a表示添加白噪声幅值，i=1，2，…，Ne，Ne表示添加白噪声对数。

（2）分别对和进行一阶LCD分解，得到一系列和}，通过对2Ne次试验集成平均得到

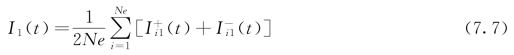
（3）检测I1（t）是否是高频间歇或噪声，如果是，再分别对和进行下一阶LCD分解，直至第p阶分量Ip（t）不是高频间歇或噪声，将已分解的前p-1个分量从原始信号S（t）中分离，得到剩余信号r（t），即

（4）再对剩余信号r（t）进行完整LCD分解。

其中，第（3）步高频间歇或噪声的检测方法是基于排列熵的随机性检测，通过设置排列熵阈值（设为0.6）来实现分解的自适应性，但是排列熵阈值的选择具有主观性，且添加白噪声幅值和数目也依据主观选择，本节对PELCD方法进行了如下方式的改进。

①向待分解信号S（t）添加一对幅值为ak但符号相反的白噪声，其中ak=0.05k SD，k=1，2，…，8，SD为原始信号的标准差，集成次数Ne固定为100（即添加白噪声对数为50）。

②对加噪信号执行完整LCD分解再集成平均，依据分解正交性指标（IO）最小和得到的分量个数最少选择最优分解结果。

③i=1，计算最优分解每一阶ISC分量Ii（t）排列熵值PEi。

（I）i=i+1。若i=p时，PEp-1＞0.6且PEp＜0.4，则对剩余信号rp-1（t）=S（t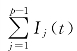）-进行完整LCD分解；

（II）若0.6≥PEp≥0.4，则分别对剩余信号rp-1（t）和rp（t）进行完整LCD分解，再依据IO最小选择分解结果；

（III）若0.6≥PEp-1＞PEp≥0.4，则对剩余信号rp-2（t），rp-1（t）和rp（t）分别进行完整LCD分解，再依据分量正交性最小选择分解结果，依此类推。(www.xing528.com)

由于PELCD成对地添加白噪声，减小了噪声残留，保证了分解的完备性，同时通过及时检测间歇或噪声等引起分解模态混叠的高频信号，避免了不必要的集成平均，不但能够抑制模态混叠，而且使得更多分量满足ISC判据条件。

7.4.1.2　仿真分析

为了说明PELCD的有效性，首先考虑如图7.4所示的仿真信号x=x1+x2，其中x1=cos（2π10t），x2是由两段频率为100 Hz，幅值为0.1的正弦信号构成的间歇信号。

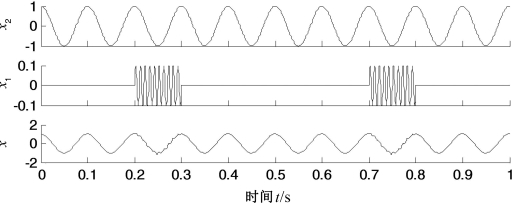
图7.4　仿真信号x及各成分的时域波形

首先，分别采用LCD和PELCD对混合信号分解，结果分别如图7.5和图7.6所示，图中Ci表示第i个ISC分量，ri表示剩余项。由图7.5可以看出，LCD分解出现了严重的模态混叠，得到的ISC分量失去了物理意义。而由图7.6可以看出，PELCD能够有效和准确地将余弦信号从高频间歇中分离出来，C3对应真实分量x1。为了说明PELCD抑制模态混叠的能力，采用公认的抑制分解模态混叠效果比较有效的EEMD方法对上述信号进行分解，结果如图7.7所示。从图7.7中可以看出，虽然EEMD也能够将余弦信号从高频间歇信号中分离出来，但是分解出现了虚假分量C3和C5，其中C4和C5具有相同的频率。因此，比较而言，PELCD分解结果是最优的。

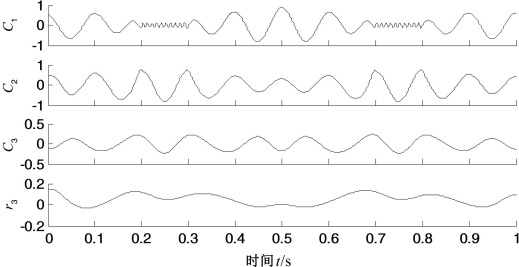
图7.5　仿真信号x的LCD分解结果

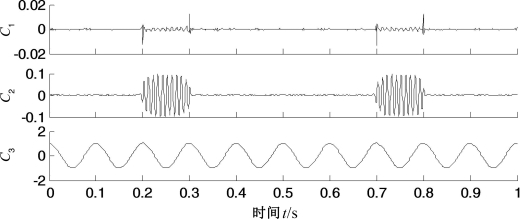
图7.6　仿真信号x的PELCD分解结果

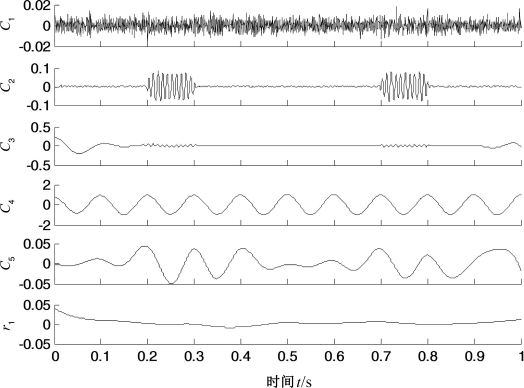
图7.7　仿真信号x的EEMD分解结果

由于调制与冲击是机械发生故障的两种典型形式[244]，因此，构造图7.8所示故障模拟信号，其中x1（t）为背景干扰噪声，x2（t）为故障高频冲击信号，x3（t）表示恒定转速正弦信号，x4（t）为调制信号，x5（t）为趋势项，x（t）为前五者的混合信号。采用PELCD对混合信号x（t）进行分解，结果如图7.9所示。由图7.9可以看出，PELCD分解得到的分量I1（t），I2（t），I3（t），I4（t）和趋势项r4（t）分别对应为x1（t），x2（t），x3（t），x4（t）和趋势项x5（t），除了第一个背景噪声分量外，其他分量与真实信号的相关性系数分别为0.976 7，0.993 9，0.986 9和0.998 7。这说明PELCD能够从混合信号中精确地提取出冲击、转速和调制成分，因此，PELCD适合处理滚动轴承振动信号。

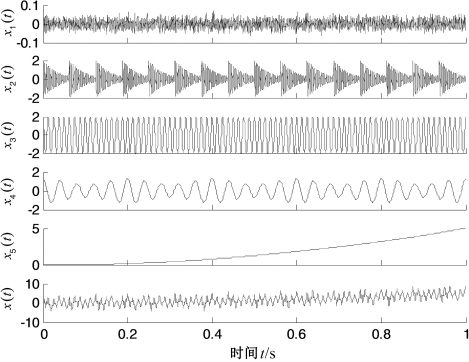
图7.8　故障模拟信号及各成分时域波形

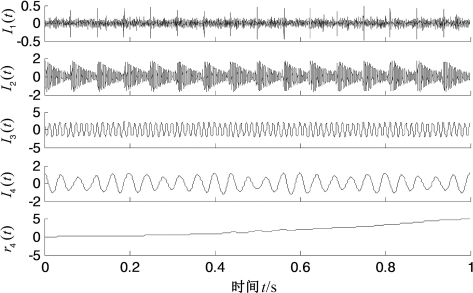
图7.9　故障模拟信号PELCD分解结果