基于LCD和排列熵的滚动轴承故障诊断

如前文所述，多尺度分析的途径有两种，一种是基于信号自适应分解的方式，另一种是通过时间序列的粗粒化方式。上文研究了多尺度排列熵在滚动轴承故障诊断中的应用，下文通过自适应分解的方式来实现多尺度分析，从而提出了一种基于LCD和排列熵的滚动轴承故障诊断方法，步骤如下。

（1）采用LCD方法自适应地将滚动轴承振动信号分解为若干个不同尺度的ISC分量：ISC1，ISC2，…，ISCn。每个分量都包含了原始信号不同频段和不同尺度的故障信息。

（2）由于故障信息一般集中在振动信号相对较高的频段，因此本节选取包含主要故障信息前五个的ISC分量，计算它们的排列熵，作为个体神经网络的特征向量：

（3）依据特征向量对多类故障滚动轴承建立神经网络集成（neural network ensemble，NNE）分类器[208，209]，通过对样本进行训练和测试，从而实现滚动轴承故障的智能诊断。

基于LCD，PE和NNE的滚动轴承故障诊断方法流程如图6.19所示。

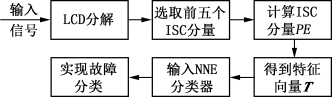
图6.19　基于LCD，排列熵和NNE的滚动轴承故障诊断方法流程图

本节将提出的方法应用于滚动轴承试验数据以证明方法的有效性。分析数据采用美国凯斯西储大学电气工程试验室的滚动轴承试验数据。测试轴承为6205-2RSJEM SKF深沟球轴承，电机负载约为735.5 W，轴承转速为1 772 r/min，试验使用电火花加工技术在轴承上布置单点故障，故障直径为0.355 6 mm，深度为0.279 4 mm，在此情况下采集到正常、内圈单点电蚀、外圈单点电蚀和滚动体单点电蚀，四种状态的振动信号，信号采样频率为12 k Hz，每种状态取30组数据，数据样本长度为2 048。正常（NORM）、滚动体故障（REF）、内圈故障（IRF）和外圈故障（ORF）四种状态轴承的振动加速度信号如图6.20所示。

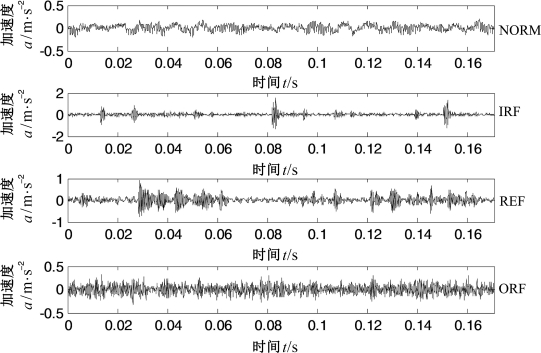
图6.20　正常和具有故障滚动轴承振动信号的时域波形(www.xing528.com)

正常、外圈故障、内圈故障和滚动体故障四种状态轴承的振动信号，每种状态取30组数据样本，其中20组用来训练，10组用来测试。首先，对四种状态的120个样本数据进行LCD分解，每个样本分解得到若干个ISC分量；其次，对包含主要故障信息的前五个ISC分量计算其排列熵，并将熵值组成特征向量，因此，共得到120个特征向量。图6.21给出了正常和三种故障轴承振动信号特征向量的关系。

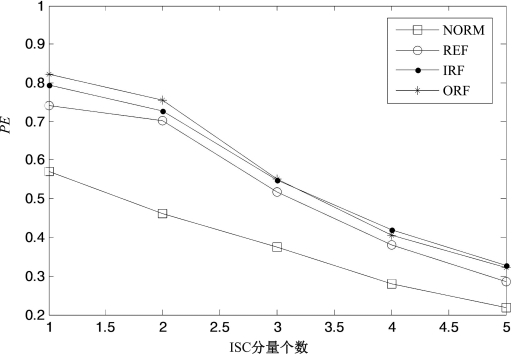
图6.21　正常和具有故障轴承的振动信号的特征向量

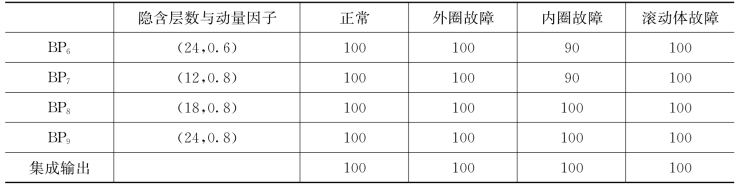
从图6.21可以发现，正常状态滚动轴承的振动信号各分量的排列熵较小，当滚动轴承发生故障时，信号各分量的排列熵值发生了较大变化。这是因为当滚动轴承发生故障时，信号的随机性发生改变，振动信号的动力学行为也发生较大突变，因此熵值变大，然而，至于是外圈故障、内圈故障还是滚动体故障，三者的区分仍不明显。因此，为了实现故障类别的诊断，本节建立基于神经网络集成的滚动轴承多故障分类器。采用训练样本分别对每个BP神经网络进行训练，再将测试样本输入到已训练的神经网络分类器中，并通过相对多数投票法集成神经网络的输出，结果如表6.8所示。

表6.8不仅说明本节提出的方法有较高的故障识别率，对试验数据达到100%，而且也说明集成后的神经网络的泛化能力确实得到了提高，NNE输出的准确率比单个输出要高和稳定。

为了说明进行多尺度分析的重要性，采用原始信号的排列熵作为特征向量，训练9个个体BP神经网络，参数选择与上述选取相同，同样的方法集成输出，四种状态的故障识别率分解为：正常100%，外圈故障70%，内圈故障80%，滚动体故障100%。这说明，直接对原始信号提取排列熵作为特征向量的分类效果并不理想，也验证了本节方法中进行LCD多尺度分解的必要性。

表6.8　个体BP神经网络和神经网络集成输出识别率比较（识别率%）

续表