多尺度排列熵在滚动轴承故障诊断中的优势

在上述理论的基础上，本小节将MPE应用于滚动轴承故障振动信号的分析。

试验数据采用美国凯斯西储大学（CWRU）轴承数据中心提供的滚动轴承试验数据[146]。测试轴承为6205-2RSJEM SKF深沟球轴承，电机负载约为2 206.496 3 W，转速为1 730 r/min，采用电火花加工技术在轴承上布置单点故障，故障直径为0.533 4 mm，深度为0.279 4 mm。在此情况下采集到正常（normal，NORM），内圈故障（inner race fault，IRF），外圈故障（outer race fault，ORF）和滚动体故障（rolling element fault，REF）四种状态滚动轴承的振动信号各30组数据，数据长度为2 048，采样频率为12 k Hz，四种状态滚动轴承的振动信号典型时域波形如图6.17所示。

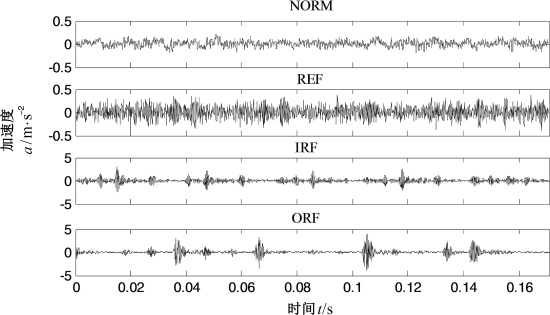
图6.17　正常和不同故障轴承振动信号的时域波形

从图6.17中不易发现正常和故障轴承振动信号的明显区别，尤其是正常和滚动体故障，内圈故障和外圈故障。首先对振动信号进行MPE分析，设置参数：嵌入维数m=6，时延λ=1，最大尺度因子为12，四种状态滚动轴承的MPE画成尺度因子的函数，如图6.18所示。

图6.18　正常和故障滚动轴承振动信号的多尺度排列熵(www.xing528.com)

当尺度因子等于1时，MPE即为原始振动信号的排列熵，由于熵值比较接近，无法明显地区别三种故障和正常轴承的类型，因此有必要对振动信号进行多尺度分析。基于此，提出了一种基于MPE和SVM的滚动轴承故障诊断方法，该方法以多尺度排列熵值为特征参数，同时基于SVM建立多故障分类器。如果采用全部的12个特征值进行训练会造成信息的冗余，且训练比较耗时，也需要较多的训练样本，且由图6.18也可以看出，前几个尺度的熵值表征了振动信号的主要信息，因此，采用前四个尺度的排列熵值作为特征向量，即T=（PE1，PE2，PE3，PE4）。本节提出的故障诊断步骤如下。

首先，提取特征参数。对振动信号进行MPE分析，提取特征参数向量T。正常、滚动体故障、内圈故障和外圈故障四种状态，每种状态取30个样本，故每种状态可得到30个表征故障特征的特征向量，共得到120个特征向量。

其次，训练分类器。由于有三种故障状态和正常状态，建立由四个SVM组成多故障分类器，SVM1为正常对三种故障分类器，SVM2为外圈故障对其他类分类器，SVM3为内圈故障对其他类分类器，SVM4为滚动体故障对其他类分类器。每种状态随机抽取10个样本进行训练，并将每组30个样本全部用来测试。基于SVM的多故障分类器如上文6.4节图6.13所示。

最后，测试分类器。对已训练的SVM分类器，将全部样本作为测试样本进行测试，输出结果如表6.7所示。

表6.7　测试样本的输出结果

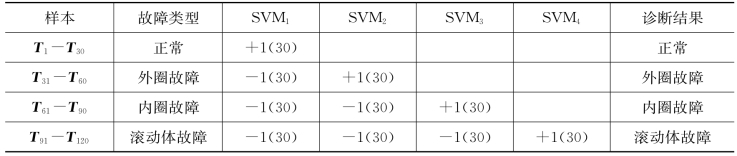
由表6.7可以看出，本节提出的滚动轴承故障诊断方法有很好的识别率，对试验数据的全部样本的识别率为100%，这验证了本节滚动轴承故障诊断方法的有效性。需要说明的是，本节选取特征值为前四个尺度上的特征值，主要基于以下原因考虑。如果特征值过少，不能完全反映故障的特征信息，而特征值过多会造成信息冗余，且需要增加训练样本和训练时间。Zhang等在文献[195]中，选择多尺度熵值的统计量，最大值、最小值、代数平均、几何平均和标准差作为特征向量，但统计量方法忽略了特征值之间的内在关系，因此，本节采用前四个尺度因子的排列熵值组成特征向量。