【摘要】：而对m=5而言，数据长度分别为1 024和256的信号的排列熵相差0.051 66，此时，数据长度为256已经可以估计合理的排列熵值。图6.14不同长度白噪声的排列熵图6.15高斯白噪声信号在不同时延下的排列熵时延λ对时间序列的计算影响较小，以长度为512的高斯白噪声信号为例，在不同λ下的排列熵值随嵌入维数的变化关系如图6.15所示，由图可以看出，时延对信号熵值的影响较小，本节取λ=1。表6.6不同长度高斯白噪声的排列熵在不同嵌入维数下的差值
排列熵的计算与时间序列长度N，嵌入维数m和时延λ的值都有关系。一般地，嵌入维数m取3～7，如果m等于1或2，此时重构的向量中包含的状态太少，算法失去意义和有效性，不能检测序列的动力学突变；如果m过大，相空间的重构将会均匀化时间序列，此时不仅计算比较耗时，而且也无法反映序列的细微变化，综上，本节选取m=6。时延λ对时间序列的计算影响较小，取λ=1。为研究数据长度N对PE计算的影响，分别以长度为128，256，512，1 024和2 048的白噪声为例，对应的PE分别记为PE1，PE2，PE3，PE4和PE5，如图6.14所示。
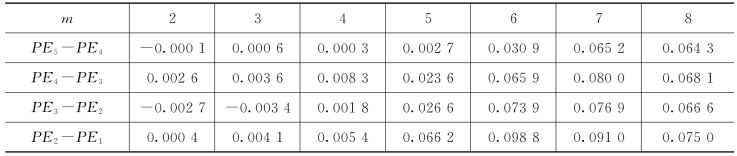
由图6.14和表6.6可以发现，嵌入维数m=6时，长度为1 024和512的两个数据的熵值相差0.065 9，而数据长度为2 048和1 024的两个信号的PE值相差0.030 9，因此，此时选数据长度为1 024较合适。而对m=5而言，数据长度分别为1 024和256的信号的排列熵相差0.051 66，此时，数据长度为256已经可以估计合理的排列熵值。一般地，嵌入维数越小，数据长度则要求越小。
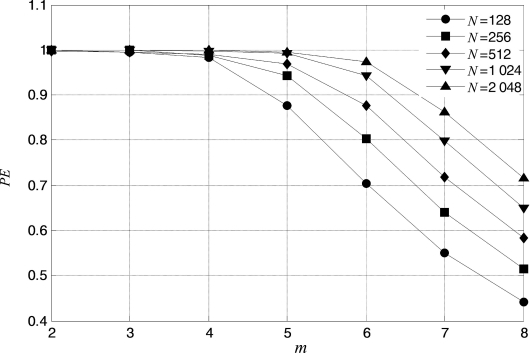
图6.14 不同长度白噪声的排列熵
(https://www.xing528.com)
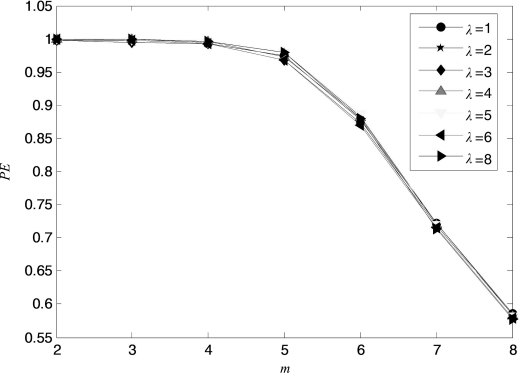
图6.15 高斯白噪声信号在不同时延下的排列熵
时延λ对时间序列的计算影响较小，以长度为512的高斯白噪声信号为例，在不同λ下的排列熵值随嵌入维数的变化关系如图6.15所示，由图可以看出，时延对信号熵值的影响较小，本节取λ=1。
表6.6 不同长度高斯白噪声的排列熵在不同嵌入维数下的差值
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
