滚动轴承故障诊断的多尺度模糊熵分析方法

由于大部分滚动轴承故障振动信号是非线性和非平稳信号，具有复杂的调幅调频和调相等调制特点，且不同故障类型的振动信号复杂性不同，如上所述，可以用模糊熵表征滚动轴承振动信号的复杂性的变化。但是由于不同故障类型特征频段不同，同一故障的故障特征信息也可能分布在多个频段和尺度，不同尺度下信号的复杂性也不相同，仅仅对原始振动信号进行模糊熵分析，并不能完全反映故障的全部特征和本质，而对振动信号进行多尺度分析是一种有效可行的分析手段。

常用的多尺度分析的途径主要有两种。一种是上述提到的，通过式（6.7）和式（6.19）粗粒化方式，将原始时间序列依据尺度因子粗粒化为若干个粗粒化序列，再通过对每个粗粒化序列进行分析，从而实现对原始信号的多尺度分析。另一种多尺度分析的途径源于小波变换的信号分解方法[204，205]。众所周知，小波变换是一种多分辨多尺度分析方法，小波变换的母函数通过调整尺度参数来实现多尺度的分析，小波的层数分解，事实上即是将信号按尺度分解。后来发展的经验模态分解（EMD）和局部特征尺度分解（LCD）等都是自适应地将一个复杂信号分解为从高频到低频分布的若干个单分量信号（IMF或ISC）之和，每个单分量信号事实上也对应原始信号在不同尺度的分量。多尺度分析减少了振动信号间特征信息的干涉或耦合，实现了故障特征的分离，同时也更方便地提取故障的本质信息。

本节分别对两种多尺度分析的思路进行了研究：（1）自适应分解的思路：提出了一种基于LCD自适应分解，模糊熵和支持向量机（support vector machine，SVM）的滚动轴承故障诊断方法，即，首先采用LCD将振动信号分解为多个不同尺度的ISC分量之和，再提取每个ISC模糊熵，最后，通过适合小样本分类的SVM建立多故障分类器，从而实现滚动轴承故障的智能诊断。（2）粗粒化思路：将多尺度模糊熵应用于滚动轴承振动信号分析，研究滚动轴承不同故障振动信号的复杂性特征。试验表明，两种方法都能够有效地区分滚动轴承的故障类型。对振动信号进行多尺度分析是一种有效的很有应用前景的故障诊断方法。

6.4.4.1　基于LCD，模糊熵和SVM的滚动轴承故障诊断

基于LCD，模糊熵和SVM的滚动轴承故障诊断方法，步骤如下：

（1）采用LCD方法将滚动轴承的振动加速度信号自适应地分解为若干个ISC分量，每个分量都包含了原始信号不同频段的故障信息，因此通过提取每个ISC分量特征即可得到原始信号的故障特征。

（2）由于故障信息一般集中在高频段，因此选取前M个包含主要故障特征信息的ISC分量，计算其模糊熵，作为特征向量T=（FuzEn1，FuzEn2，…，FuzEnM）。

（3）建立基于SVM的对应三类故障的分类器，通过对分类器进行训练和测试，实现故障诊断。

为了说明该方法的有效性，将其应用于试验数据分析。仍采用第6章第3节部分描述的6307型滚动轴承试验数据。首先，取正常滚动轴承、具有外圈故障和内圈故障三种状态的原始振动信号，每种状态取5个样本数据，共15个样本数据，分别计算每个样本的模糊熵，以及五组模糊熵的均值，结果如表6.3中第1列所示。从中可以看出，原始信号的模糊熵值虽然可以区分正常、外圈故障和内圈故障三种状态的滚动轴承，但两种故障状态的模糊熵值比较接近，区分效果不明显。正常滚动轴承的振动信号的模糊熵值最大，约为2左右。这是因为正常的滚动轴承的振动是随机振动，无规则程度较高，信号较为复杂，因此，熵值较大。当出现故障时，系统出现规律性和周期性冲击，振动信号的自相似性增强，熵值降低，因此具有外圈故障和内圈故障的轴承振动信号的模糊熵值比正常状态的要低。另外，具有内圈故障滚动轴承的振动信号熵值较具有外圈故障的大，这是因为外圈相对较固定，冲击特征和周期性特征更明显，而内圈随轴一起转动，理论上后者故障机理比前者要复杂，熵值要大。但不足的是，通过振动信号本身的模糊熵值区分故障类型的效果不明显。

表6.3　不同状态滚动轴承振动信号及其前5个ISC分量的模糊熵

由于原始振动信号的模糊熵的区分效果不明显，因此考虑对每组原始振动信号进行LCD分解，每组数据分解得到约10个ISC分量，由于前几个分量包含了原始信号的主要故障信息，因此，计算每组数据分解得到的前五个分量的模糊熵，每种状态五组数据的前五个分量的模糊熵均值，如表6.3中第2～6列所示。从中可以看出，具有内圈故障的滚动轴承信号分解得到的ISC2，ISC3和ISC4的模糊熵值比具有外圈故障振动信号分解得到的对应分量的熵值大，但都小于正常轴承振动信号对应的分量的模糊熵值。因此，多个分量的模糊熵能够区分故障类型。为了实现故障的智能诊断，考虑采用适合小样本分类的SVM建立多故障分类器。

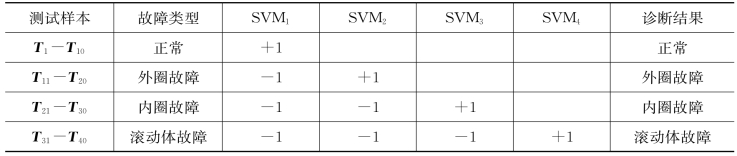
正常、具有外圈故障和内圈故障三种状态轴承的振动信号，每种类型分别选择13组数据，由此共得到39个故障特征向量T用于滚动轴承的故障模式识别。其中，每种状态9组数据用来训练样本，其余用来测试。试验数据有三种状态，需建立能够识别三种状态的多故障SVM分类器，该分类器由三个SVM组成。其中，SVM1为正常滚动轴承对故障类分类机，SVM2为外圈故障对其他故障分类机，SVM3为内圈故障对其他故障分类机，核函数选用径向基核函数。在分类测试中，先将测试样本的特征向量T输入SVMl，若判别式f（x）输出为“+1”，则确认为正常，测试结束；否则自动输入SVM2，直到SVM3，若输出不为“+1”，则说明测试样本属于其他故障，测试样本输出结果如表6.4所示。表6.4中测试样本全部得到正确识别，故障识别率是100%，这说明本节提出的方法是一种有效的滚动轴承故障诊断方法。

表6.4　测试样本输出和诊断结果

6.4.4.2　多尺度模糊熵在滚动轴承故障诊断中的应用

滚动轴承故障诊断的关键是从振动信号中提取特征信息。振动信号一般是非平稳信号，含有干扰信号和噪声，但模糊熵的计算具有抗噪和抗干扰能力，因此，考虑直接对原始信号进行多尺度模糊熵分析，由此提出了基于多尺度模糊熵和支持向量机的滚动轴承故障诊断方法，即，首先对振动信号的原始振动信号进行多尺度模糊熵分析，观察正常状态和故障状态的多尺度模糊熵曲线的区别，尤其是区分效果比较明显的前几个尺度；其次，若区别明显，则可以实现故障类型的诊断，否则，选取前M个尺度的多尺度模糊熵作为特征参数，输入支持向量机分类器，通过对样本进行训练和测试，从而实现滚动轴承的故障诊断。

试验数据采用美国凯斯西储大学电气工程试验室的滚动轴承试验数据[146]。测试轴承为6205-2RSJEM SKF深沟球轴承，电机负载约为735.5 W，轴承转速为1 797 r/min，使用电火花加工技术在轴承上布置单点故障，故障直径为0.533 4 mm，深度为0.279 4 mm，试验数据采集装置如图6.10所示。在此情况下采集到正常、内圈单点电蚀、外圈单点电蚀和滚动体单点电蚀四种状态的振动信号，信号采样频率为12 k Hz，每种状态截取20组数据，数据样本长度为2 048。正常（NOR）、滚动体故障（BRF）、内圈故障（IRF）和外圈故障（ORF）四种状态轴承的典型振动加速度信号如图6.11所示，图中从上到下依次为：NOR，BRF，ORF和IRF。

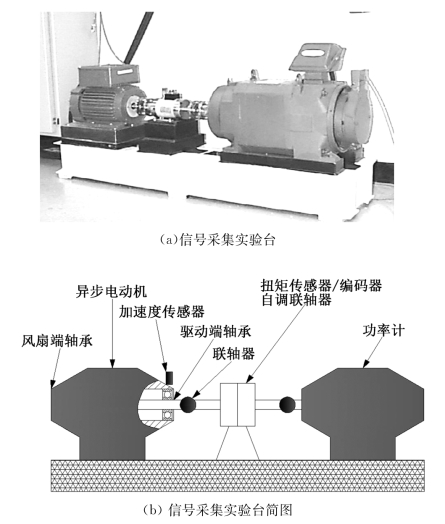
图6.10　信号采集实验台及简图

(www.xing528.com)

图6.11　四种状态轴承振动信号的时域波形

由于干扰和背景噪声的影响，从时域波形上不易发现四种状态的明显区别。为了避免诊断的偶然性和盲目性，从以上四种状态的每种状态中随机抽取3组数据，共12组数据，分别在三组不同参数条件下，对上述12组数据进行多尺度模糊熵分析，结果如图6.12（a），（b）和（c）所示。

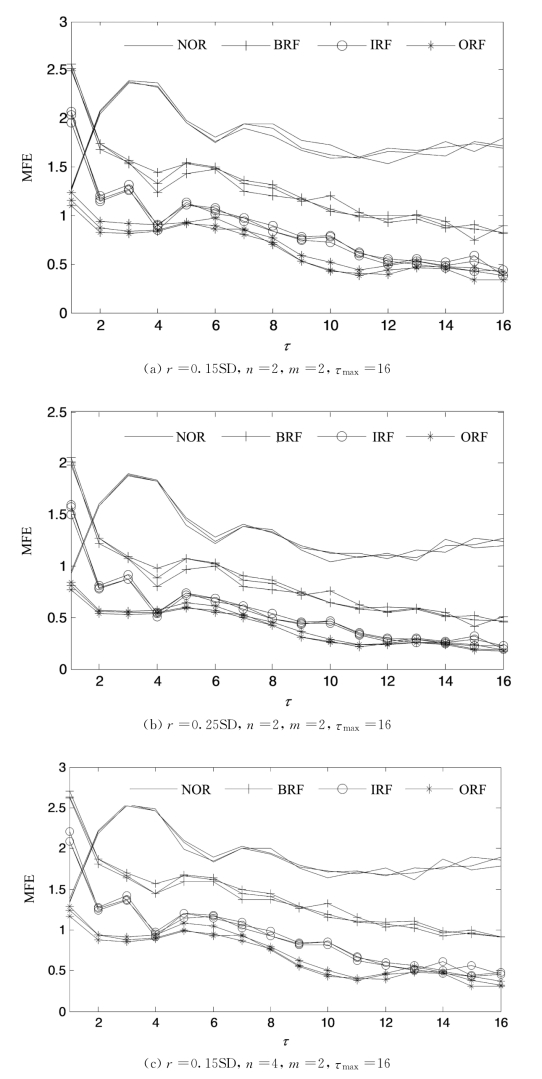
图6.12　不同状态滚动轴承振动信号在不同参数条件下的多尺度模糊熵

从图6.12中可以得出如下结论。

首先，在大部分尺度（τ＞1）上四种状态滚动轴承的振动信号被明显地区分开来。正常滚动轴承的振动加速度信号的模糊熵值比三种故障状态振动加速度信号的熵值大，这是因为正常滚动轴承的振动是随机振动，其振动信号在大部分尺度上无规则程度较高，自相似性较低，相对较复杂，故熵值较大；当出现故障时，振动信号的规则性增强，自相似性增高，大部分尺度上熵值降低。

其次，在大部分尺度（τ＞1）上，四种状态滚动轴承的振动信号的熵值关系是：E（NOR）＞E（BRF）＞E（IRF）＞E（ORF）。当滚动轴承出现故障时，振动信号自相似性较高，熵值降低；由于轴承工作时外圈相对固定，当外圈发生故障时，振动信号冲击性和自相似性较强，因此，熵值较低。而当发生内圈故障时，振动信号也表现出一定的冲击性和自相似性，但其冲击频率比发生外圈故障时的冲击频率要大，且由于内圈随轴转动，振动信号的不规则性更强，因此，理论上讲，具有内圈故障的轴承振动信号的复杂性程度要比与具有外圈故障的轴承的振动信号的复杂性程度高，故障机理也更复杂，因此其振动信号的熵值要比具有外圈故障的要大。而当滚动体发生故障时，滚动体既有自转，又随轴转动，振动波形冲击性与内圈和外圈故障相比也更为不规则，振动信号更为复杂，其振动信号要较具有内圈和外圈故障轴承的振动信号复杂、自相似性低，因此，具有滚动体故障的滚动轴承的振动信号的熵值在大部分尺度上要比具有内圈和外圈故障的熵值大。但如上所述，三种故障状态滚动轴承的振动信号的熵值在大部分尺度上都要小于正常滚动轴承振动信号的模糊熵值。

第三，特别要说明的是，在尺度因子等于1时，多尺度模糊熵即是原始信号的模糊熵，此时正常滚动轴承振动信号的模糊熵值比具有故障的轴承振动信号的熵值小，但这并不能说明具有故障滚动轴承的振动信号比正常轴承的振动信号复杂，相反，这恰好说明了进行多尺度分析的必要性[195]。三种故障状态的轴承的振动信号的多尺度模糊熵随着尺度因子的增加而逐渐递减，而正常轴承的振动信号多尺度模糊熵随着尺度因子的增加而先增后减，且在大部分尺度上熵值变化不大。这说明单一尺度上的模糊熵值并不能反映故障的本质，其他尺度的序列上也包含有重要的故障特征信息。

第四，从图6.12中可以看出，参数r增大，对应的熵值变小；n增大，对应的熵值变大；但参数的改变不影响四种状态轴承振动信号多尺度模糊熵值的相对关系，只是熵值的大小略有不同，这说明多尺度模糊熵具有很好的相对一致性。

以上分析说明，机械振动信号在其他多个尺度上包含有重要的时间模式信息，而单一尺度上的信息并不能反映故障的本质，这说明进行多尺度分析的重要性，而这一点是分形维数和模糊熵等无法反映的，这也是多尺度模糊熵优于传统的基于单一尺度熵分析之处。

上述只是从每种状态的轴承振动信号中随机选取三组数据的分析结果，样本量较少，有一定的偶然性，为了验证方法的普适性，选用适合小样本分类且训练时间较短的支持向量机（SVM）作为分类器，提出了一种新的滚动轴承故障诊断方法，步骤如下：

（1）对轴承原始振动信号进行MFE分析，得到τmax=16个熵值，并画成尺度因子的函数；

（2）根据MFE曲线诊断滚动轴承的故障类别，若故障类型区分不明显，则依图选择特征参数的个数，由于用全部熵值作为特征参数信息会有冗余，从图6.13中可以看出前5个模糊熵值即可有效地区别故障类型，因此本节选取前5个熵值作为特征量，即T=[En1，En2，…，En5]；

（3）将特征向量T输入支持向量机进行训练和测试，从而实现滚动轴承故障类别的诊断。

具有外圈故障、内圈故障、滚动体故障和正常四种状态的滚动轴承，每种状态分别选取20组数据，共80组数据，由上述方法共得到80个故障特征向量。其中每种状态10组特征向量用来训练，其余10组作为测试样本。该试验有4种滚动轴承状态，故需建立4个二类支持向量分类机，按照图6.13所示，组合成可以识别4种状态的多分类SVM分类器。图6.13中，SVM1为正常滚动轴承对其他类分类机，SVM2为外圈故障状态对其他故障分类机，SVM3为内圈故障对其他故障分类机，SVM4为滚动体故障对其他故障分类机。f（x）表示支持向量机的最优分类函数，核函数选用径向基核函数。在分类测试中，将测试数据样本的特征向量T依次输入已训练的SVM1，若判别式f（x）输出为“+1”，则确认为正常，测试结束；否则自动输入SVM2，直到SVM4，若输出不为“+1”，测试样本属于其他故障。

图6.13　基于SVM多故障分类器示意图

将每一类的10个测试样本（共40个测试样本），输入到已训练的SVM分类器进行测试，测试样本的诊断结果如表6.5所示，测试样本全部得到正确识别，识别准确率为100%。

表6.5　测试样本诊断结果

多尺度模糊熵和模糊熵、多尺度熵、分形维数等类似，都是对信号复杂性和自相似性的量度，但与它们相比，多尺度模糊熵能够反映蕴含在时间序列更深层的模式信息，且具有计算所需数据短、抗噪能力强和具有相对一致性等优点。研究了多尺度模糊熵在滚动轴承故障诊断中的应用，提出了一种基于多尺度模糊熵和SVM的滚动轴承故障诊断新方法。试验数据表明，多尺度模糊熵能够有效地反映滚动轴承的故障特征和区别故障类型，是一种有效的滚动轴承故障诊断方法。