由模糊熵的定义,模糊熵值的计算和嵌入维数m,相似容限r,模糊函数的梯度n和数据长度N都有关系。
(1)嵌入维数m。和近似熵和样本熵一样,一般取嵌入维数m=2。因为m越大,在序列的联合概率进行动态重构时,会有越多的详细信息,但m越大,计算所需要的数据长度就更长(N取10m~30m),因此综合考虑,m=2。
(2)相似容限r。r表示模糊函数边界的宽度。r过大会丢失掉很多统计信息;r过小估计出的统计特性的效果不理想,而且会增加对结果噪声的敏感性。一般r取0.1SD~0.25SD(SD是原始数据的标准差),本节取r=0.15SD。
(3)n的选取。n决定了相似容限边界的梯度,n越大则梯度越大,n在模糊熵向量间相似性的计算过程中起着权重的作用。当n>1时,更多地计入较近的向量对其相似度的贡献,而更少地计入较远的向量的相似度贡献,n过大会导致细节信息的丧失;当n<1时则相反,事实上,n趋于无穷大时,指数函数即变为单位阶跃函数。为了捕获尽量多的细节信息,建议计算时取较小的整数值,如2或3等。综上考虑,本节取n=2。
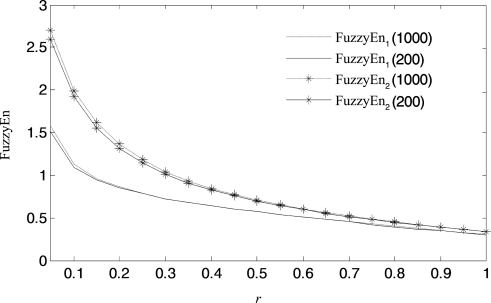
(4)数据长度N。一般熵值结果对数据的长度要求不高,若选定m=2,则N取100~900。仍以式(6.18)所示信号为例,分别考虑p=0.1和0.3时两个混合信号不同长度的模糊熵,如图6.7所示,从图中可以看出,数据长度是200或者1 000,对两混合信号的模糊熵值几乎没有影响,这说明模糊熵计算所需的数据长度短。
(5)另外,对于多尺度模糊熵还有一个参数,尺度因子τ,一般地,τ的最大值大于10即可,因为原数据长度为N,则粗粒化后的序列长度为N/τ,一般要保证N/τ具有的长度不影响模糊熵值的计算(一般大于100)[173,187]。
 (https://www.xing528.com)
(https://www.xing528.com)
图6.7 不同长度下两混合信号的模糊熵
对于一个自相似随机过程,功率谱密度S(f)与频率f成比例关系,即S(f)∝1/fβ。其中,β=0时随机过程为白噪声信号,β=1时随机过程称为1/f噪声,二者在自然界都很常见[194-195]。白噪声与1/f噪声的时域波形和傅里叶谱分别如图6.8所示。从图中可以看出,1/f噪声是长程相关的(long-range correlation),这意味着1/f噪声要比白噪声信号更为复杂,二者的MSE和MFE如图6.9所示。
从图6.9可以看出,当尺度因子τ等于1时,白噪声的样本熵和模糊熵值都比1/f噪声的大,如果依据单一尺度的熵的观点,很容易得出白噪声比1/f噪声复杂的错误观点。但是,随着尺度因子τ的增加,白噪声的样本熵和模糊熵值都逐渐递减,而1/f噪声的熵值则趋于平稳,而且随着尺度因子的增加,在大部分尺度上,1/f噪声的样本熵和模糊熵都大于白噪声的样本熵和模糊熵(τ>3时和τ>5时),这意味着1/f噪声要比白噪声更为复杂。此外,随着尺度因子的增加,两个信号的模糊熵变化较为平缓,而它们的样本熵则波动较大,因此,多尺度模糊熵要比多尺度熵更加稳定,一致性更好。

图6.8 白噪声和1/f噪声的波形和频率

图6.9 白噪声与1/f噪声的MSE和MFE
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




