转子系统作为典型的旋转机械,常发生的故障类型主要有转子不对中、不平衡、碰摩和油膜涡动及振荡等[199-202],且各个故障的系统都表现为非线性振动,因此,转子系统故障诊断的关键是如何从非线性的振动信号中提取与故障特征密切相关的信息[10,199-201,203]。多尺度熵作为一种衡量时间序列复杂性的动力学参数,能够反映时间序列在不同尺度的复杂性程度和规则性程度,本节考虑将多尺度熵用于分析具有故障的转子系统径向振动信号。
从转子振动模拟试验台上分别采集转子不平衡、正常、不对中、碰摩和油膜涡动五种状态下的径向位移振动信号(实验装置见图3.6)。采样频率为2 048 Hz,采样时间为0.5 s,转速为3 000 r/min。五种状态的时域波形分别如图6.4所示。
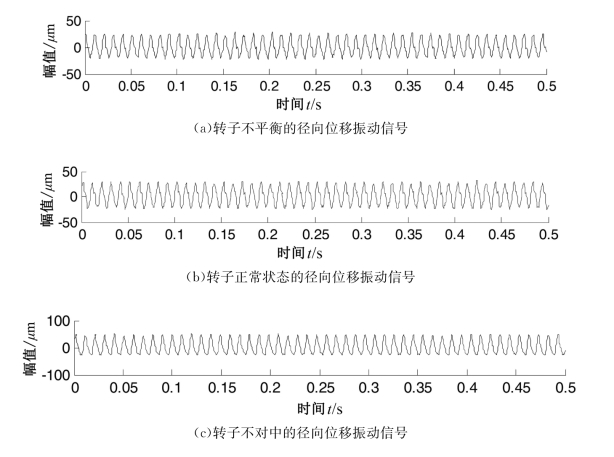

图6.4 转子系统不同状态的径向位移振动信号
从图6.4中转子系统五种状态径向位移信号的时域波形上不易发现它们的明显区别,因此考虑它们的样本熵值的关系。以上五种状态转子径向位移信号每种状态取三个数据样本计算样本熵再求平均值,结果如表6.2所示。
表6.2 五种状态转子振动信号的样本熵
 (https://www.xing528.com)
(https://www.xing528.com)
从表6.2可以看出,不同故障转子系统的径向位移振动信号的样本熵不同,同种故障类型的位移信号的样本熵比较接近。故障状态与正常状态的转子振动信号的熵值大小关系是:
![]()
碰摩和不平衡的样本熵值相对较大,这说明二者的振动信号的复杂性较高,而不对中和油膜涡动的样本熵值相对较小,这说明二者的振动信号的复杂性较低,序列自相似性较高。由上知,样本熵可以实现不同故障的区分,但由于各种故障类型的样本熵值相差较小,区分效果不明显。
考虑分析转子系统振动信号的多尺度熵特征,仍然通过分析上述五种状态下的各三组样本,分别求其多尺度熵,并画成尺度因子的函数,如图6.5所示。从图6.5中可以得出如下结论:首先,与样本熵相比,由于引入尺度因子,多尺度熵能够更明显更直观地区分转子的几种故障状态类型。不同的故障类型的转子径向位移信号在不同尺度下的熵值不同;其次,多尺度熵值和样本熵所得的结果是一致的。但不同故障状态与正常状态的多尺度熵值区分非常明显,大小关系是:
![]()
此外,图6.5说明,具有碰摩故障转子径向位移信号在大部分尺度上的熵值比正常滚动轴承的熵值较高,无规则程度更高,信号更为复杂,不平衡和正常轴承次之,不对中和油膜涡动故障径向位移信号在大部分尺度上的熵值较小,这说明不对中和油膜涡动状态径向位移信号自相似性较高,信号较为规则;第三,五种状态的多尺度熵曲线都是随着尺度因子的增加,而渐变地趋向于某一值,这说明,多尺度熵不仅能够很好地反映时间序列的复杂性程度,而且还反映了时间序列隐藏在其他尺度上的信息,而这一点是分形维数和样本熵等单一尺度的分析方法无法反映的,这也体现了多尺度分析的优越性。
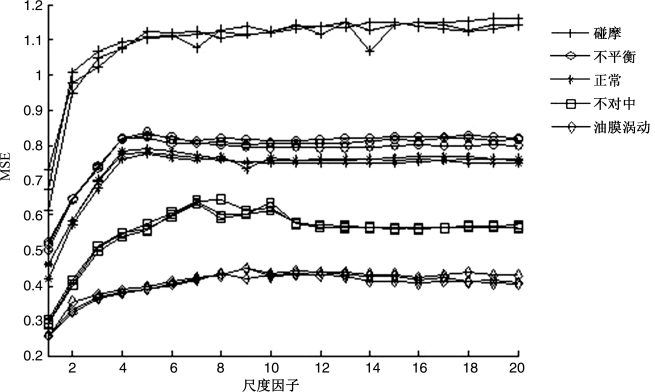
图6.5 转子五种状态振动信号的多尺度熵
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




