仿真信号分析技术概述

为了说明GEMD和IEAD-NQ的优越性，首先考察式（5.34）所示的仿真信号：

其中，x1（t）=3（t+1）cos（2π50t+2π5t2），x2（t）=e-tcos（2π28t），x3（t）=2t2。x（t）由调幅调频信号、调幅信号和一个多项式趋势项叠加而成，各分量和混合信号的时域波形如图5.16所示。

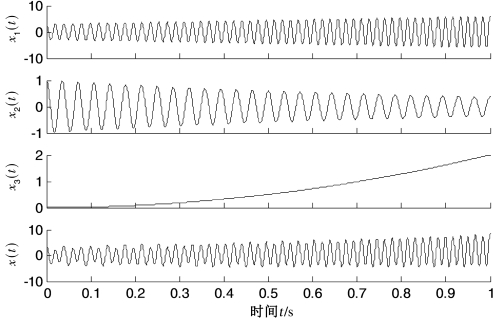
图5.16　式（5.34）所示仿真信号x（t）及其各成分时域波形

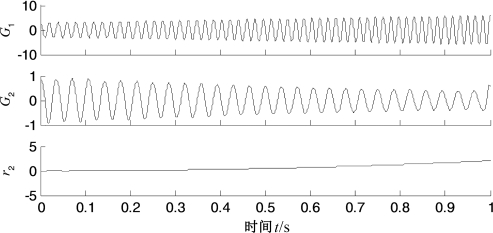
分别采用EMD和GEMD对x（t）进行分解，结果分别如图5.17和图5.18所示。图5.17中，c1和c2表示EMD的第1和第2个IMF，r2表示对应剩余项；图5.18中，G1和G2表示GEMD的第1和第2个GIMF，r2表示对应剩余项。

由图5.17和图5.18可以看出，EMD和GEMD都能够有效地将三个单分量成分从混合信号中分离，从波形上看，二者的分解效果都比较好，无明显差别。为了比较分解效果，图5.19给出了两种分解结果与真实分量的绝对误差，即分解得到的分量与对应真实分量之差的绝对值，图中实线表示由GEMD得到的GIMF与真实分量的误差，虚线表示由EMD得到的IMF分量与真实分量的误差，Errori表示第i个分量与对应真实值xi（t）的绝对误差。由图5.19可明显看出，由EMD得到的IMF分量c1和c2与对应真实分量x1（t）和x2（t）的绝对误差较大，远大于由GEMD得到的GIMF分量G1和G2与对应真实分量x1（t）和x2（t）的绝对误差。不仅如此，由EMD分解得到的趋势项r2也与真实分量x3（t）的绝对误差较大，大于由GEMD得到的趋势项与x3（t）的绝对误差，且有较严重的端点效应。此例表明，与EMD相比，GEMD有更好的精确性，得到的分量与真实分量更吻合。

图5.17　式（5.34）所示仿真信号x（t）的EMD分解结果

(www.xing528.com)

图5.18　式（5.34）所示仿真信号x（t）的GEMD分解结果

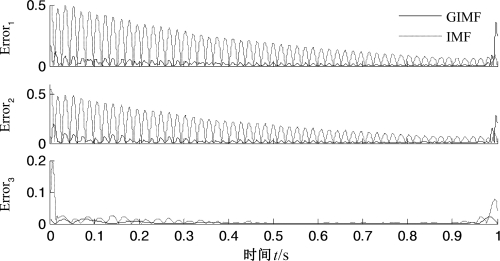
图5.19　EMD和GEMD两个分量的绝对误差

为了说明IEAD-NQ方法解调的优越性，分别采用HT与IEAD方法估计x1（t）和x2（t）瞬时幅值，采用NQ和NHT方法估计它们的瞬时频率，估计结果如图5.20（a）和图5.20（b）所示，其中，估计值与真实值的绝对误差分别如图5.21（a）和图5.21（b）所示。由图5.20（a）和图5.20（b）可以发现，由HT和IEAD估计得到的瞬时幅值二者无明显差别，但由HT估计的瞬时幅值有明显的端点效应；由图5.21（a）和图5.21（b）可以看出，NHT估计得到的瞬时频率有严重的端点效应，且“污染”向信号内部传播，而NQ方法相对端点效应较小，瞬时频率较为平滑，与真实值绝对误差也较小。

综上，与HHT相比，基于GEMD和IEAD-NQ的解调方法在信号分解和解调的精确性等方面都有很大的提高，是一种有效信号解调方法。

图5.20　HT和IEAD估计的x1（t）和x2（t）瞬时幅值和绝对误差

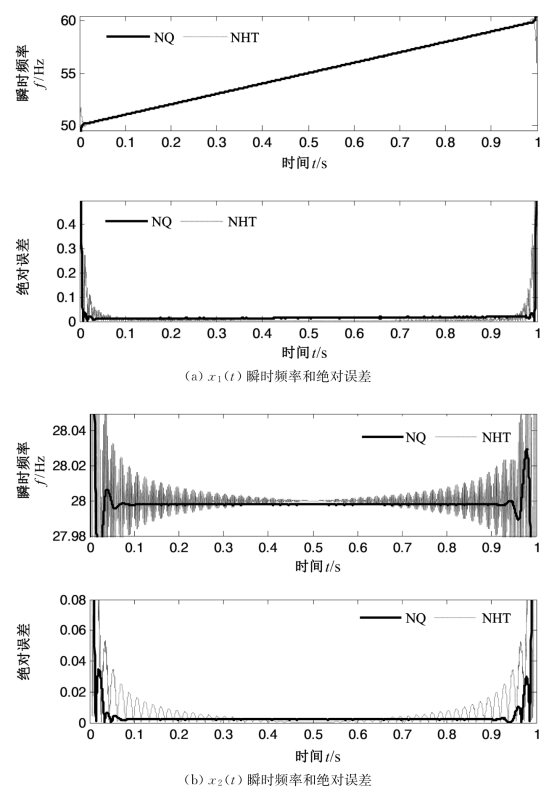
图5.21　NQ和NHT估计的x1（t）与x2（t）瞬时频率和绝对误差