经验包络法（EE）：优化绩效评估方法

5.2.3.1　经验调幅调频分解

一般单分量信号x（t）未必是形如a（t）cosφ（t）[a（t）＞0，φ′（t）＞0]的形式，而将其写作调幅部分和调频部分的乘积的形式对于求瞬时频率是非常重要的，能量算子解调和反余弦法以及标准希尔伯特变换也都基于此假设，因此有必要研究将任意单分量信号唯一地分解写作调幅和调频部分的乘积形式的一般方法。

Huang等在文献[129]中提出了一种将单分量信号特别是内禀模态函数分解成调幅部分和调频部分乘积形式的方法，称之为经验调幅调频分解（EAD），详细步骤如下。

（2）采用三次样条函数拟合所有（τk，xk），得到信号的经验包络函数a11（t）。

对于一般实信号x（t）来说，它的极值点是固定的，因此经验包络函数也是唯一确定的。用得到的经验包络函数对数据进行标准化，即将x（t）除以经验包络函数a11（t），得

（3）x1（t）是标准化后的信号，理论上x1（t）的经验包络函数a12（t）应该小于等于1，否则，对x1（t）重复上述步骤n次，直到a1n（t）≤1时停止迭代，此时x1n（t）为纯调频信号。

记纯调频信号x1n（t）为F（t），则存在φ（t）（φ′（t）＞0），使得

（4）x（t）的调幅部分定义为

至此，x（t）被分解为调幅部分与调频部分乘积的形式。

上述标准化的过程经验化地实现了单分量信号的调幅调频的分解。一般地，上述过程收敛比较快，迭代次数不会太多，一般2～5次即可实现数据的标准化。如经验模态分解一样，上述方法只是经验性的分解，并没有解析的表达式和严格的数学证明。另外，分解过程可能会引起原始信号波形的失真，但失真的总和是可以忽略不计的，因为上述过程有过零点周期性地严格控制，而过零点的位置是不变的[129]。(www.xing528.com)

5.2.3.2　经验包络法

由EAD，任意单分量信号x（t）可以近似写作x（t）=a（t）F（t）=a（t）cosφ（t）的形式，F（t）的瞬时频率即为原始信号的瞬时频率，因此，只要求出F（t）的瞬时频率即可。由此提出了如下的经验包络法。

（1）由EAD，任意单分量信号x（t）可写作x（t）=a（t）cosφ（t）。

（2）令F（t）=cosφ（t），并对其两边求导，得

由于φ′（t）=2πf（t）一般是线性的，或相对载波部分变化缓慢的函数，因此可视φ′（t）=2πf（t）为F′（t）的包络部分。

（3）对F′（t）进行EAD分解，得

这里的b（t）近似为式（5.15）中的φ′（t），原信号的瞬时频率定义为

经验包络法基于信号的EAD分解提出，计算简单方便，不需要复杂的程序和极值点处的特殊处理，只要两次应用EAD和一次求导即可。经验包络法的核心是EAD分解的效果直接决定了求得的瞬时频率的准确性。这里有个矛盾，为了得到纯调频信号，则需要增加迭代的次数，但由于采用三次样条拟合包络，迭代的次数增加，拟合的误差会增大，求得的瞬时频率误差也会随之增大；如果迭代的次数过少，那么三次样条拟合的误差减小，得到的纯调频信号的个别点仍大于1。试验表明，经验包络法对信号的纯调频程度要求不高，即允许有个别点的值大于1，对结果影响很小。经验包络法流程如图5.1所示。

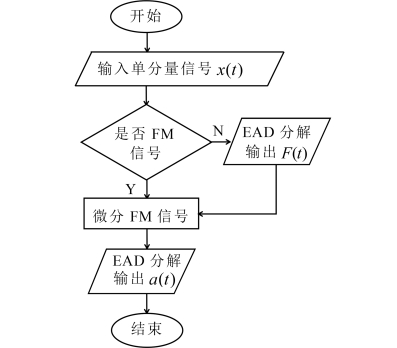
图5.1　经验包络法流程图

事实上，由EAD信号被分解为调幅部分和纯调频部分的乘积，对于纯调频信号F（t）=cosφ（t），可以采取类似于LMD方法中的反余弦法求取瞬时频率，即对F（t）=cosφ（t）两边求反余弦，得φ（t）=arccos F（t），φ（t）相位以2π展开，再对其求导得到瞬时频率。基于反余弦法求瞬时频率直接方便，不需要希尔伯特变换，且计算量较小，但反余弦法的缺点是其求得的瞬时频率在信号的极值点处会有不稳定的突变，需要平滑处理；并且对信号的标准化要求较高，如果标准化后的数据有大于1的点，那么在该处反余弦法估计结果会有很大的突刺和误差。