应用实例：PEEMD在滚动轴承故障信号分解中的表现

为了说明本节提出的PEEMD方法的实用性，考察具有故障的滚动轴承实测信号，试验数据来自美国Case Western Reserve University（CWRU）轴承数据中心。试验所用数据为具有内圈故障的滚动轴承振动加速度信号，故障频率fi约为162.2 Hz，转速为1 797 r/min，因此转频fr约为29.95 Hz，采样频率为12 k Hz，采样时长0.25 s，其时域波形如图4.47所示。

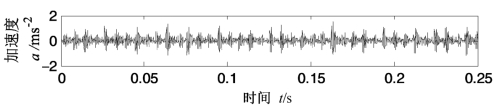
图4.47　具有内圈故障的滚动轴承振动信号的时域波形

分别采用EMD，CEEMD和PEEMD对上述信号进行分解，限于篇幅，EMD和CEEMD分解结果不再画出，PEEMD分解结果如图4.48所示。其中CEEMD和PEEMD分解中添加噪声幅值和对数分别为0.1和100。

从图4.48中可以发现，PEEMD分解对模态混叠有一定的抑制，分解的分量较为合理。不仅如此，经计算发现，PEEMD的分解重构误差也非常小，幅值数量级为10-15，完备性较好。为了说明PEEMD的优越性，分别对EMD，CEEMD和PEEMD得到的各个分量做包络谱分析。研究发现，EMD，CEEMD和PEEMD分解的前两个IMF分量的包络谱中，故障特征频率处的谱线都很明显，并且还有明显的2倍频谱线，三者都能够实现故障的诊断，无明显区别。而三者的第四个IMF分量的包络谱，如图4.49所示，图中横轴最大分析频率应为6 000 Hz，为了便于观察，进行了10倍放大，EMD分解所得第四个IMF分量没有特别明显的谱线，2倍转频线也不明显；CEEMD的第四个IMF分量中有明显的转频倍频和故障特征频率谱线，但其他频率干扰较大，而且，在100 Hz处的干扰谱线无法解释，另外，相对高频200～300 Hz部分谱线干扰也较大；而PEEMD分解的第四个IMF分量包络谱中，2倍转频和故障特征频率谱线较为明显，干扰频率较少。因此，从这方面来说，PEEMD方法具有一定的优势。(www.xing528.com)

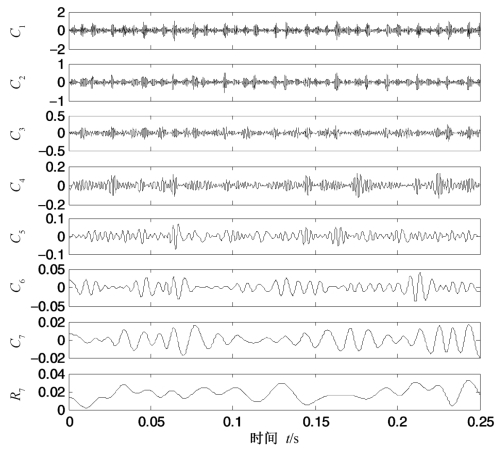
图4.48　滚动轴承振动信号PEEMD分解结果

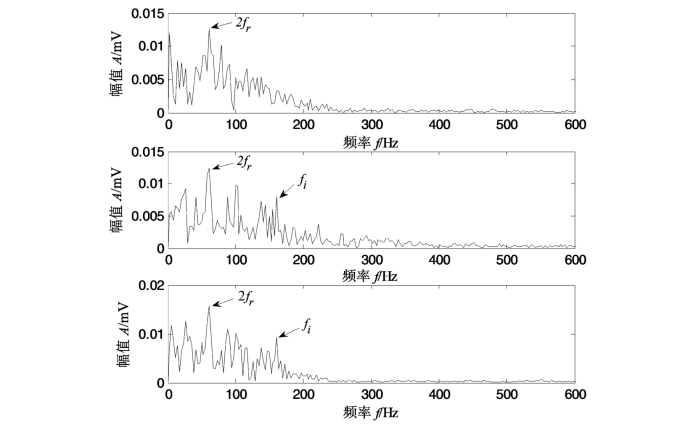
图4.49　从上到下依次为EMD，CEEMD和PEEMD分解的第四个IMF的包络谱

针对EEMD和CEEMD方法不能完整解决EMD中模态混叠的问题，本节基于排列熵的随机性检测，提出了改进的EEMD方法——部分集成局部特征尺度分解（PEEMD）。通过对仿真信号和实测信号分析，结果表明，PEEMD不但能够有效地抑制EMD分解过程中的模态混叠，而且还节省了EEMD和CEEMD分解过程中的计算量，缩小了由于添加白噪声引起的重构误差，保证了得到的分量满足IMF的定义。PEEMD方法中，为了提高PEMD分解的自适应性，在选择参数检测分解得到的异常信号时，提出了基于排列熵的随机性检测，通过选择适当的排列熵阈值，可以实现PEEMD的异常信号检测和自适应分解。当然，基于排列熵的检测方法不是唯一的，理论上选择更合适的平稳性信号检测方法会更好地提高PEEMD的分解效果。