为了说明PEMD方法的有效性和实用性,本节将PEMD方法应用于具有碰摩故障的转子径向位移振动信号分析。考虑具有碰摩故障的转子模拟信号,采样频率为2 048 Hz,采样时间为0.5 s,转速为3 000 r/min,fr=50 Hz,时域波形如图4.33所示,图4.34是其幅值谱,从中只看到主要频率成分为转频50 Hz和其3倍频,与故障有关的频率成分则不明显。
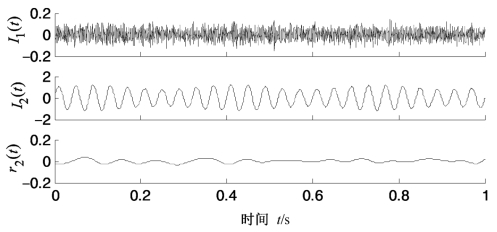
图4.31 图4.29所示混合信号的PEMD分解结果

图4.32 EEMD和PEMD得到的与真实分量x2(t)对应的分量的绝对误差
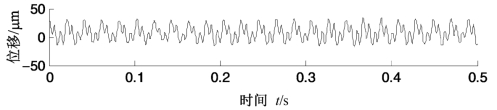
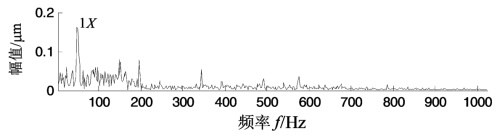
图4.33 具有局部碰摩故障的转子径向位移振动信号
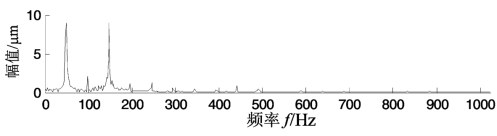
图4.34 图4.33所示的转子径向位移振动信号的幅值谱
采用PEMD对上述振动信号进行分解,结果如图4.35所示。从图中可以看出,分解得到的第一个分量I1(t)具有调制特征,I1(t)包含了碰摩故障的主要成分。对I1(t)求其包络谱,如图4.36所示,从中可以看出,I1(t)的调制波频率为转频50 Hz,这是由于转子每旋转一周动件与静件就要摩擦一次造成的。I2(t)是转频的3倍频,I3(t)是转频,I4(t)为1/5分倍转频的3倍频,I4(t)也进一步证实转子出现了碰摩故障[8,110,132]。
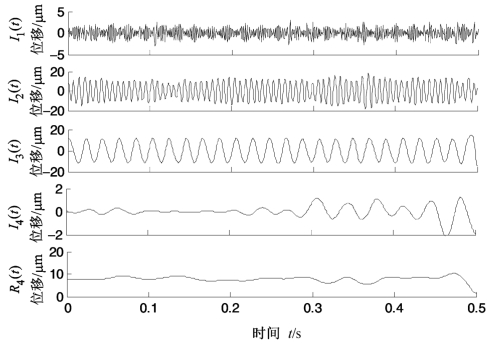
图4.35 图4.33所示转子振动信号的PEMD分解结果
 (https://www.xing528.com)
(https://www.xing528.com)
图4.36 PEMD分解第一个分量I1(t)的包络谱
上述分析说明,PEMD能够有效地从转子故障位移振动信号中分离出故障成分和转频成分。为了说明PEMD的优越性,采用EMD对相同转子位移振动信号进行分解,结果如图4.37所示。由图中波形可以看出,EMD分解的第一个分量I1(t)与第二个分量I2(t),第二个分量I2(t)和第三个分量I3(t)都发生了局部模态混叠。虽然能够从第一个分量I1(t)的包络谱(图4.38)中看出50 Hz的调制成分,但诊断效果不如PEMD分解第一个分量的明显。因此,与EMD相比,PEMD具有一定的优越性。上述结果表明,PEMD不仅对仿真信号有很好的分析效果,而且还能够有效地应用于转子碰摩故障的诊断,且效果优于EMD方法。
本节提出了一种基于伪极值点假设的经验模态分解(PEMD)来抑制EMD的模态混叠问题,并将其应用于转子碰摩故障的诊断,仿真和实测信号分析结果表明PEMD方法与EMD和传统的抑制模态混叠的方法EEMD相比,至少有如下优点:
(1)与EMD相比,PEMD能够有效地抑制EMD分解的模态混叠问题,使得到的分量更具有物理意义;
(2)与EEMD相比,PEMD分解得到的分量与真实信号的相关性更好,更吻合真实值,且分解的正交性也更好;
(3)PEMD不需要添加白噪声和确定添加白噪声的幅值和数目,是一种完备的和自适应的信号分解方法;
(4)PEMD能够从振动信号中有效地提取与故障特征有关的分量,有效地应用于机械设备故障诊断。
PEMD是一种很有应用前景的数据分析方法,适合于机械设备故障振动信号的处理,但不足之处在于,PEMD也有端点效应,镜像延拓不是最理想的,仍需要进一步研究。
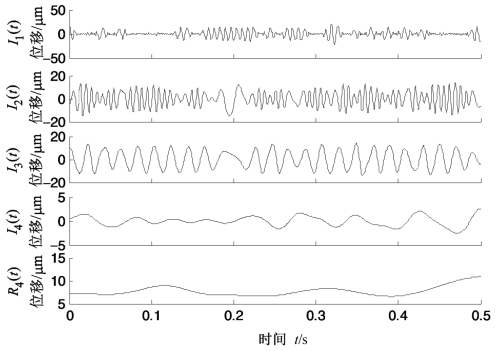
图4.37 图4.33所示转子振动信号的EMD分解结果
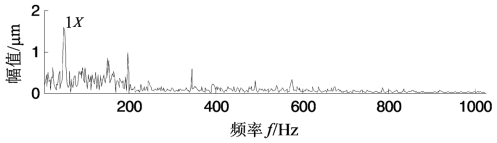
图4.38 EMD分解第一个分量I1(t)的包络谱
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




