基于伪极值点假设的经验模态分解（PEMD）优化技术

EMD分解发生模态混叠时，尺度差异较大的信号被分解到同一个IMF分量中，因此，限制分解过程中的尺度将会对模态混叠有很好的抑制，基于此，本节提出了一种基于伪极值点假设的经验模态分解（PEMD）方法。

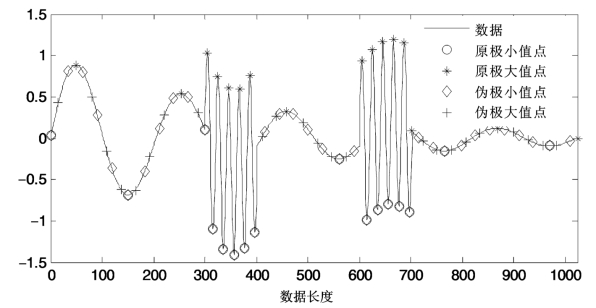
图4.23　一个仿真信号的伪极值点示意图

基于伪极值点的定义，PEMD的分解过程如下：

（1）确定原始信号x（t）所有极大值点和极小值点，通过上述方式确定x（t）所有伪极值点，将得到的伪极大值点视为极大值点，将得到的伪极小值点视为极小值点。(www.xing528.com)

（2）分别采用三次样条拟合所有极大值点和极小值点，得到上包络线e1（t）和下包络线e2（t），并计算二者的均值曲线，即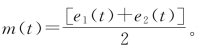

（3）将均值曲线m（t）从原始信号中分离出来得到剩余分量u（t），即

若u（t）满足IMF分量的定义，记为I1（t），否则，视u（t）为x（t），重复上述步骤，直到u（t）满足IMF分量的定义，记为I1（t）；将I1（t）从原始信号中分离，得到剩余项r（t）=x（t）-I1（t）。

（4）将r（t）视为原始数据，重复上述步骤（1）～（3），直到剩余信号r（t）满足筛分终止条件。

上述步骤（3）中需要选择合适的IMF判据，PEMD通过最小极值尺度度量所有极值尺度来增加伪极值点，每次提取出信号中尺度最小也即瞬时频率最高的分量[131]，也正因为如此，由于端点效应的影响，PEMD会分解出频率较大，且幅值较小的信号。为了抑制这种情况的产生，本节选择限制迭代次数的方法来终止迭代。一般地，迭代次数限制为6～10次，也可以依据不同的分量限制不同的迭代次数。第（4）步中原EMD方法中的筛分终止条件是剩余信号的极值点个数不超过两个，但是由于三次样条拟合易引起包络过冲和不足，导致过多的虚假分量的产生，因此，本节考虑采用如下筛分终止条件：剩余信号的极值点个数少于3或者剩余信号的能量与原信号能量比小于千分之一。

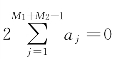特别地，当所有小于2δ时，即伪极值点总数时，信号中尺度未发生混淆，此时PEMD即等同于原EMD方法。PEMD不需要EEMD的事先设置添加噪声的幅值和数目，因此，PEMD是一种完备的、自适应的信号分解方法。