仿真与实测信号分析比较

为了说明ELCD和PELCD方法的有效性和合理性，下面我们通过仿真信号进行验证，考虑式（4.17）所示信号：

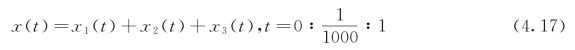
其中，x1（t）=（t2+1）cos（2π40t），x2（t）=cos（2π15t）；x3（t）是幅值为0.4、频率为200 Hz和幅值为0.2、频率为150 Hz的两段正弦信号组成的高频间歇信号。

分别采用ELCD，CEEMD和PELCD对式（4.17）所示的仿真信号进行分解，结果分别如图4.15，图4.16和图4.17所示。ELCD方法中，添加噪声幅值a和集成次数Ne分别为0.4和120；CEEMD方法中，a和Ne分别为0.2和120；PELCD方法中，a和Ne分别为0.4和120。

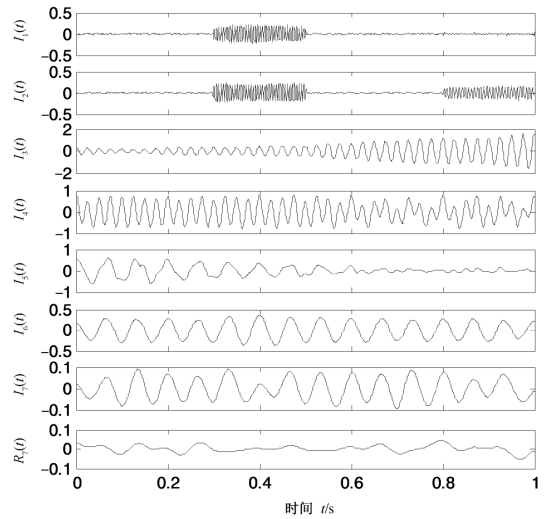
图4.15　式（4.17）所示仿真信号的ELCD分解结果

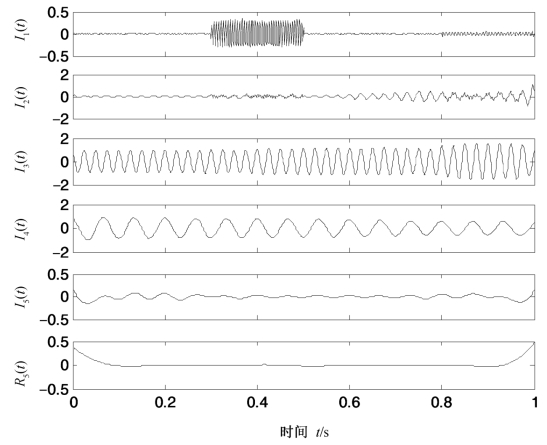
图4.16　式（4.17）所示仿真信号的CEEMD分解结果

图4.17　式（4.17）所示仿真信号的PELCD分解结果

由图4.15，图4.16和图4.17可以发现，ELCD虽然能够抑制分解过程的模态混叠，但出现了较多的伪分量，本质上仍存在模态混叠；CEEMD虽然也实现了高频间歇信号和低频分量的区分，抑制了分解的模态混叠，然而CEEMD分解的分量I2（t）包含了I3（t）成分，使得分量I3（t）与真实值x1（t）吻合较差；PELCD方法则完美地实现了高频间歇信号和低频分量的分解，前两个分量为间歇信号，I3（t）与I4（t）分别对应为仿真信号的x1（t）和x2（t）。经计算，CEEMD两个分量与真实值的相关性系数分别为0.989 7和0.993 2，而PELCD的分量与真实值的相关性为0.999 5和0.997 9。因此，综上所述，PELCD在抑制模态混叠和伪分量、提高分量的精确性方面要优于ELCD和CEEMD方法。

上述仿真干扰信号为间歇高频信号，再考虑式（4.18）所示的仿真信号：

其中，x1（t）=cos（2π40t），x2（t）=cos（2π15t），x3（t）为幅值0.1的噪声信号。

由于分量频率为常函数，波形简单，这里不再画出。分别采用CEEMD和PELCD对x（t）进行分解，分解结果如图4.18和图4.19所示，其中添加白噪声幅值为0.1，添加白噪声对数为60（即总体平均的次数为120）。

由图4.18和图4.19可以看出，CEEMD虽然分解出了噪声信号和两个低频分量，但I2（t）包含了噪声和I3（t）成分，得到的I3（t）和I4（t）与真实值也有明显的误差。计算发现，二者与真实值的相关性分别为0.976 3和0.991 0。PELCD分解的结果与真实值较为接近，误差较小，得到的分量与对应真实值的相关性分别为0.997 1和0.997 7。

为比较分解分量的瞬时特征，图4.20给出了两种分解方法得到的第三个分量I3（t）的瞬时幅值和瞬时频率，从中可以看出，CEEMD和PELCD得到的分量瞬时频率与真实频率（40 Hz）的差别都很小，但CEEMD分量的端点效应较为严重；CEEMD第三个分量的瞬时幅值波动较大，而PELCD第三个分量的瞬时幅值误差较小，更接近理论值1。(www.xing528.com)

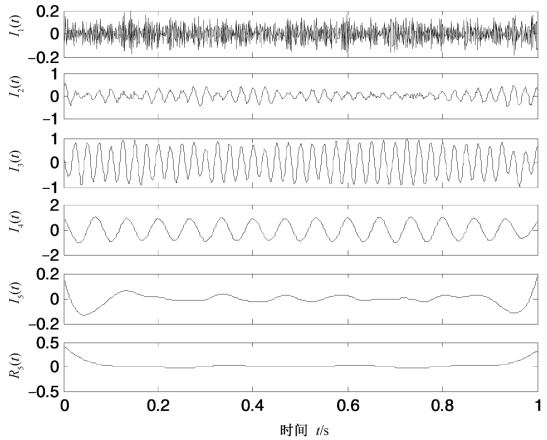
图4.18　式（4.18）所示仿真信号的CEEMD分解结果

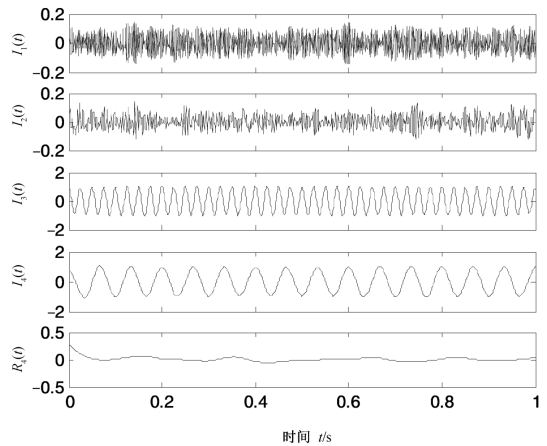
图4.19　式（4.18）所示仿真信号的PELCD分解结果

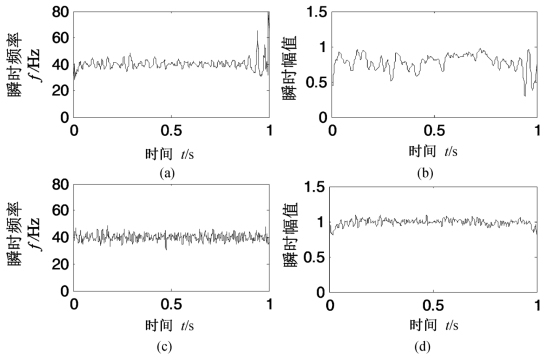
图4.20　CEEMD和PELCD得到的第三个分量的瞬时频率和瞬时幅值

上述仿真信号表明，与CEEMD相比，PELCD能够更好地抑制模态混叠，得到的分量精确性更高，是一种有效的信号分解方法。为了说明PELCD对实测信号的有效性，考虑将PELCD方法应用于Wu和Huang在原EEMD文献中分析的日长（length-of-day，LOD）数据的部分（1980年01月01日—1990年01月01日，数据幅值单位：10 000）[63]。分别采用CEEMD和PELCD对其进行分解，添加噪声幅值为0.2，集成次数为200。分解结果分别如图4.21和图4.22所示，为节约篇幅只画出了前五个分量及其剩余项。观察图4.21和图4.22易发现，二者的分解结果是相对应的。各分量的物理意义是，I1（t）平均幅值远小于其他分量，是具有拟正则的周期近似为7天峰值与随机高频波动的叠加。I2（t）平均周期为14天，I3（t）平均周期为28天等。虽然从二者分解的结果中都能得到如上周期规律，但从波形图可以看出，CEEMD分解得到的分量并不是关于横轴对称的（如图中虚线所圈部分），不是严格意义上的IMF，如分量I2（t），I4（t）和I5（t）；而PELCD分解得到的分量光滑性更好，关于横轴对称，满足ISC分量的定义，而且计算发现，PELCD各分量的上述周期特征更为明显和精确。

ELCD虽然能够在一定程度上抑制模态混叠，但分解会产生很多伪分量。PELCD则对模态混叠有更好的抑制作用。PELCD至少在以下三个方面要优于ELCD和CEEMD方法：

（1）首先，在计算时间和速度方面。PELCD只有前几个分量采用集成平均，而剩余分量则是LCD分解。因此，理论上PELCD计算时间要少于ELCD方法。

（2）其次，在抑制模态混叠和伪分量方面。ELCD和CEEMD虽然能在一定程度上抑制模态混叠，但是依赖于添加白噪声的幅值和集成次数，如果参数选择不合适，那么分解会产生较多的伪分量，而PELCD分解产生的伪分量相对较少。

（3）第三，在分解得到的分量的精确性方面。CEEMD和ELCD方法并不能保证得到的分量满足IMF和ISC分量的定义，需要后续处理。PELCD得到的分量满足ISC分量定义条件，提高了分量的精确性。

综上，理论和仿真分析结果都表明，PELCD对LCD分解中的模态混叠有很好的抑制作用，是一种有效的数据处理方法。

图4.21　LOD数据的CEEMD分解结果

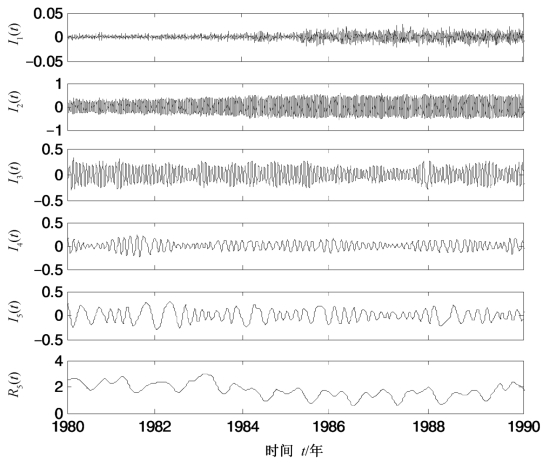
图4.22　LOD数据的PELCD分解结果