CEEMDAN与CELCD的比较分析

为了说明本章提出的方法能够有效地抑制模态混叠，只需比较LCD分解和CELCD分解即可。为了说明本章提出的方法优于传统的基于噪声辅助分析的抑制模态混叠的方法，还需将CELCD与EEMD，CEEMD和CEEMDAN进行对比。但是，文献[120]对前二者进行了详细比较，结果发现CEEMD与EEMD的分解效果基本相同，优势只体现在分解分量的完备性，而文献[121]详细阐述了CEEMDAN相比于EEMD的优势，CEEMDAN效果也要优于CEEMD，因此，本章只将CELCD与LCD和CEEMDAN进行对比。

首先，不失一般地，考虑如式（4.11）所示的混合信号：

其中x1（t）=cos（80πt），x2（t）=2cos（30πt）；t=0∶∶1；x3（t）为均值为零且服从正态分布的随机噪声，混合信号及其分量时域波形如图4.1所示。

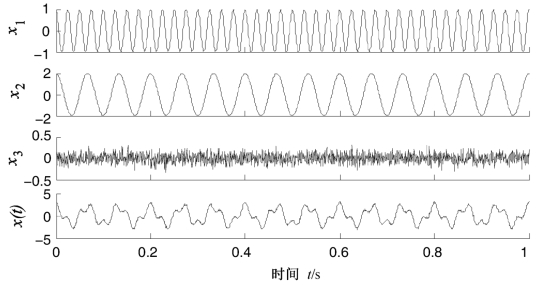
图4.1　混合信号式（4.11）及各分量的时域波形

分别采用LCD，CEEMDAN和CELCD方法对混合信号进行分解，其中ISC和IMF分量的判断依据为三阈值准则，端点处理方法为镜像延拓，三种方法分解结果分别如图4.2，图4.3和图4.4所示。图4.2中，LCD分解得到13个ISC分量和剩余项，只画出了前6个ISC分量和对应剩余项。图4.3中，CEEMDAN分解得到11个IMF分量和对应剩余项，只画出了前8个IMF分量和对应剩余项，前几个分量为不同频段噪声信号，前三个分量求和画出。CEEMDAN和CELCD中总体平均次数Ne和添加白噪声幅值a的选择如表4.1所示。为了量化地比较两种方法分解结果，考虑评价参数：分解的正交性指标IO，分量与实际分量的相关性r和能量误差E。其中，ri表示实际分量xi（t）与不同方法分解得到分量的相关性系数，能量误差Ei定义为分解得到分量与实际分量xi（t）误差的能量与实际分量能量的比值，即Ei=，E（·）为求能量算子，Ij为与xi（t）对应的分解分量，误差能量越小说明分解分量越接近实际值[128]。

表4.1　CEEMDAN和CELCD的参数对比

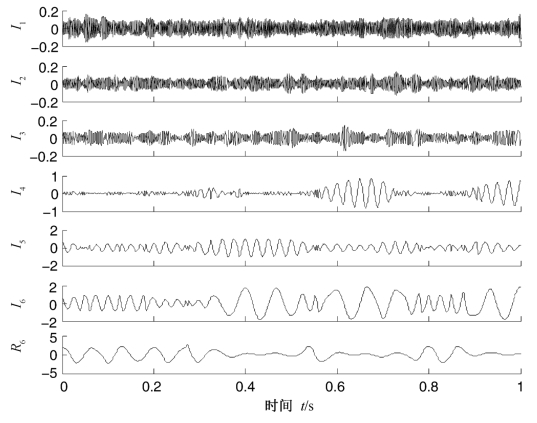
图4.2　混合信号的LCD分解结果

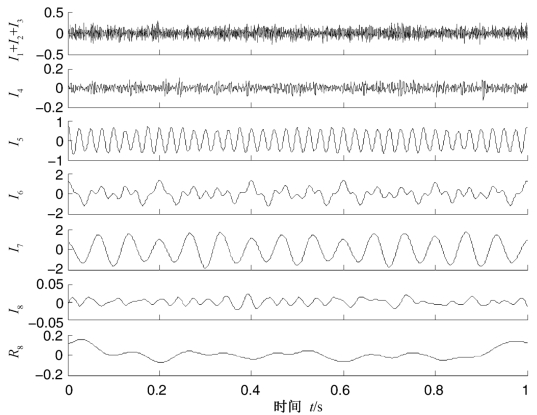
图4.3　混合信号的CEEMDAN分解结果

图4.4　混合信号的CELCD分解结果

两种方法得到的分量与实际分量的上述比较参数指标如表4.1所示。由表4.1，图4.2，图4.3和图4.4可以得到如下结论。首先，由于噪声的干扰，LCD分解出现了严重的模态混叠，得到的分量与实际误差很大，无可读性。而CEEMDAN和CELCD两种方法有效地抑制了分解的模态混叠，提取出了与实际值较为接近的分量。CEEMDAN分解的前四个是噪声信号，I5和I7分别对应为实际分量的x1（t）和x2（t），而I6则为得到的伪分量，由于总体平均时各个加噪信号得到的分量不同所致。CELCD得到的前五个分量为噪声信号，而I6和I7则对应为实际分量的x1（t）和x2（t），分解较为理想。其次，为了便于比较，两种方法选择的总体平均次数和加入的白噪声是相同的，由表4.1可以看出，CELCD得到的分量I6，I7与实际分量x1（t），x2（t）的相关性比CEEMDAN得到的分量I5，I7与x1（t），x2（t）的相关性更高，而且，CELCD得到的分量I6，I7与实际分量x1（t），x2（t）的能量误差比CEEMDAN得到的分量I5，I7与实际分量x1（t），x2（t）的能量误差更小，因此，CELCD得到的分量更吻合实际值。最后，由表4.1中也可以看出，CELCD正交性指标较小，仅为CEEMDAN的正交性指标的10%，这说明CELCD分解更具有正交性。另外，计算发现，两种分解结果的重构误差数量级皆为10-16～10-15，这说明两种分解方法都是完备的。

上述仿真信号的分析结果表明，CELCD对噪声干扰引起的模态混叠有很好的抑制作用，再考虑由间歇信号导致分解出现模态混叠的例子。(www.xing528.com)

不失一般地，考虑高频间歇与正弦信号叠加的混合信号：

mix（t）=x（t）+n（t）

其中x（t）=cos（30πt），t=0∶∶1；n（t）为两段高频间歇信号。混合信号由高频间歇信号和瞬时频率为15 Hz的余弦信号组成，它们时域波形如图4.5所示。

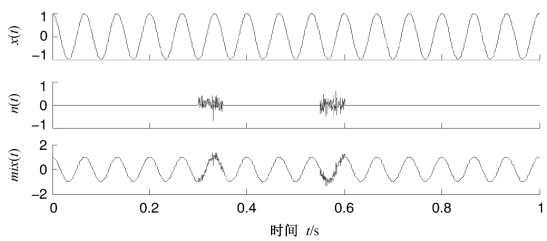
图4.5　混合信号mix（t）及其分量的时域波形

分别采用LCD，CEEMDAN和CELCD对混合信号进行分解，结果如图4.6，图4.7和图4.8所示。其中，图4.6中，LCD分解得到14个ISC分量和一个剩余项，这里只画出了前6个ISC分量和其剩余项；图4.7中，CEEMDAN分解得到12个IMF分量和一个剩余项，这里只画出了前8个分量和其剩余项；图4.8中，CELCD分解得到8个ISC分量，前5个分量为不同频段噪声，这里求和画出，R为重构误差。CEEMDAN和CELCD的总体平均次数Ne和加入白噪声的幅值a如表4.2所示。

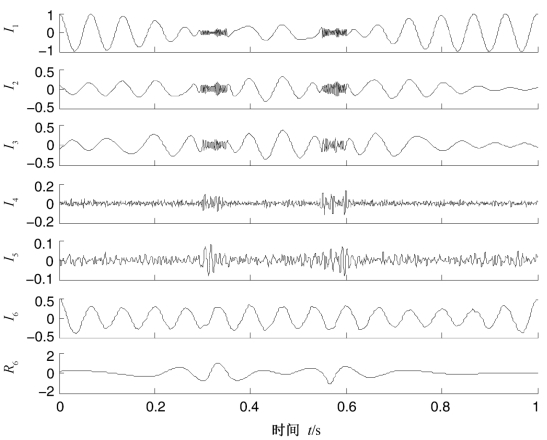
图4.6　混合信号mix（t）的LCD分解结果

表4.2　CEEMDAN和CELCD的参数对比

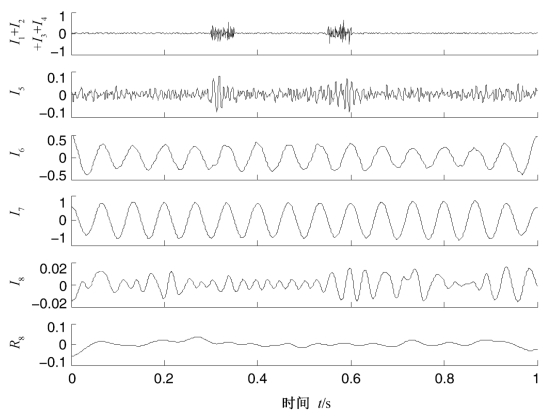
图4.7　混合信号mix（t）的CEEMDAN分解结果

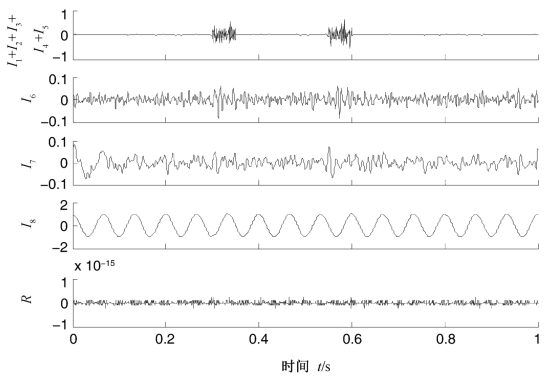
图4.8　混合信号mix（t）的CELCD分解结果

分析图4.6，图4.7，图4.8和表4.2可得到如下结论。首先，由图4.6可以看出，由于间歇信号的干扰，LCD分解出现了严重的模态混叠；由图4.7和图4.8可以看出，CEEMDAN有效地抑制了分解的模态混叠问题，提取出了与实际值较为接近的分量，但同时也出现了伪分量，实际分量x（t）被分解为两个分量之和（I6+I7）。而CELCD在分解出噪声信号之后得到的分量I8对应实际分量x（t），趋势项为零，重构误差R数量级为10-15，分解具有完备性，分解结果比较理想。其次，由表4.2可以看出，在总体平均次数和加入的白噪声是相同的情况下，CELCD得到的分量I8与实际分量x（t）的相关性比CEEMDAN得到的分量I7与x（t）的相关性更高，而相应的能量误差则更小，因此，CELCD得到的分量比CEEMDAN得到的分量更接近实际分量。第三，由表4.2知，CELCD正交性指标较小，仅为CEEMDAN的正交性指标的10%，这说明CELCD分解具有更好的分解正交性。

以上两个仿真信号分析的结果表明，CELCD不仅能够有效地抑制由于高频间歇和随机噪声引起的模态混叠，而且分解优于基于噪声辅助分析的EEMD，CEEMD和CEEMDAN方法。