完备拆分重构：仿真信号的EMD、LCD和GEMD分析

GEMD综合了EMD，ITD和LCD等六种单一均值曲线分解方法的优势，得到的GIMF分量相对于单一均值分解的方法来说是最优的。值得一提的是，GEMD并不是将待分析信号采用六种方法分解、再从结果中选择最优作为GIMF，而仍是采用类似于EMD的过程进行筛分。

由上述公式（3.14）知，GEMD是完备的，即原始信号可以通过所有GIMF分量与剩余之和进行重构。下文将通过估计重构误差进行数值化验证，其中重构误差定义为原始数据与所有GIMF分量和的差。

GEMD分解的正交性在应用过程中是很容易满足的，但理论上却很难保证。事实上，由分解的过程知，得到的分量是彼此局部正交的，因为分解是从高频到低频进行筛分，在任何的相同时刻或位置，不同GIMF的瞬时频率都不相同。GEMD分解的正交性将通过后验的数值的方法进行验证。

为了说明GEMD方法的优越性，理论上要将GEMD与上述六种单一分解方法的每种方法都进行比较，但这将占用大量篇幅，由于在这六种分解方法中EMD是最经典、最常用、也被学者研究最多的，因此，本文仅将GEMD与EMD和本书提出的LCD方法进行对比。

不失一般地，考虑式（3.15）所示的仿真信号：

其中x1（t）=[1+0.2（cos2π2t）]sin（2π40t+2π3t2），x2（t）=cos（2π24t）。信号x（t）及其两个分量成分x1（t）和x2（t）的时域波形如图3.15所示。

图3.15　式（3.15）所示仿真信号的时域波形

分别采用EMD，LCD和GEMD对式（3.15）所示的信号x（t）进行分解，结果分别如图3.16～图3.18所示。为了便于对比，图3.19给出了三种分解方法的分解绝对误差。表3.2给出了三种分解方法的正交性，前两个分量的正交性，第一个和第二个分量与对应真实值的绝对误差的能量。首先，从图3.16～图3.18可以看出，三种分解方法的分解结果波形无明显差别，其中LCD的剩余项幅值较大，EMD和GEMD的剩余项几乎为常数零。其次，由图3.19可以看出，EMD的两个IMF分量与对应真实值的绝对误差的幅值最大，绝对误差的能量指标也最大；LCD的两个ISC分量与对应真实值的绝对误差的幅值次之，绝对误差的能量指标也次之；而GEMD得到的两个GIMF分量与对应真实值的绝对误差的幅值最小，绝对误差的能量指标也最小。第三，由表3.2中正交性指标可以看出，GEMD分解正交性指标和两个分量的正交性指标也都是最小的，这说明与EMD和LCD相比，GEMD分解的正交性也是最好的。此外，为了衡量分解的完备性，定义绝对重构误差为原始信号与分解得到的所有分量之和差的绝对值，即，其中x（t）是被分解信号，Ii（t）（i=1，2，…，n）表示分解得到的分量。ARE越小说明分解的完备性越好，ARE为零则说明分解是完备的。计算上述三种分解方法的ARE，结果发现绝对重构误差数量级都在10-16～10-15，这说明三种分解都是完备的。此例表明，和EMD与LCD相比，GEMD在分解正交性和精确性等方面都有一定的优越性。(www.xing528.com)

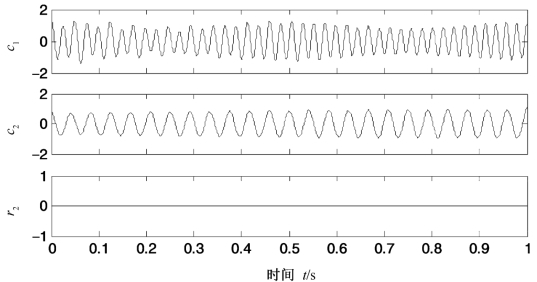
图3.16　式（3.15）所示仿真信号EMD分解结果

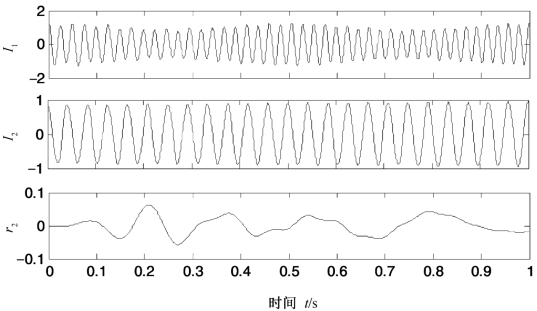
图3.17　式（3.15）所示仿真信号LCD分解结果

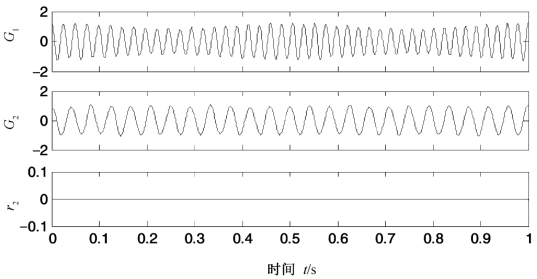
图3.18　式（3.15）所示仿真信号GEMD分解结果

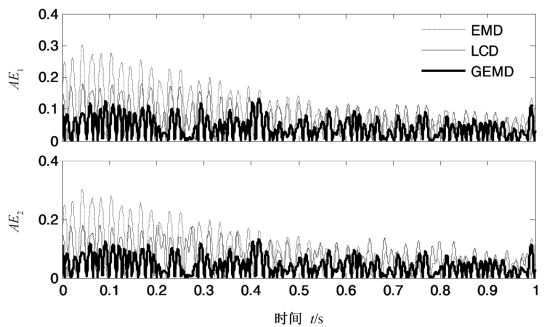
图3.19　式（3.15）所示仿真信号三种方法前两个分量的分解绝对误差

表3.2　EMD，LCD和GEMD分解结果的评价指标