EMD方法假设任何一个复杂信号可被分解为若干个瞬时频率具有物理意义的内禀模态函数(IMF)和一个趋势项之和。其中IMF满足条件:
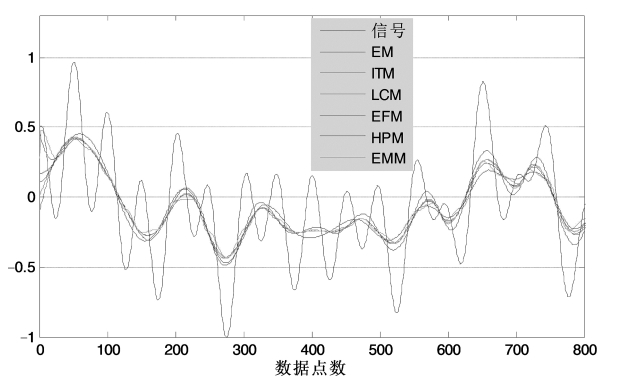
图3.13 信号不同均值曲线示例
(Ⅰ)整个数据段,极值点个数与过零点个数相等,或至多相差不超过一个;
(Ⅱ)在数据内任一点,基于三次样条拟合极大值得到的上包络线与基于三次样条拟合极小值得到的下包络线的均值为零。
条件(Ⅱ)基于信号的上下包络的平均,(Ⅰ)和(Ⅱ)保证了得到的分量瞬时频率具有物理意义。但这只是一个单分量信号瞬时频率具有物理意义的充分条件,而非必要条件,如第2章节中定义的瞬时频率具有物理意义的ISC分量条件。(https://www.xing528.com)
综合多种定义方法,本文定义一种新的单分量信号——广义内禀模态函数(generalized intrinsic mode function,GIMF),GIMF满足条件:
(a)同IMF定义条件(I);
(b)在数据的任一点,数据的均值曲线为零;
(c)满足条件(a)和(b)的分量称之为pre-GIMFs,在得到的pre-GIMFs中选择瞬时带宽与中心频率比值最小的分量作为最终的GIMF。
对于给定的信号z(t)=a(t)ejφ(t),其在t时刻的瞬时带宽定义为![]() 当Bt非常小时,z(t)被认为是窄带信号。信号z(t)的带宽可表示为两部分之和,即
当Bt非常小时,z(t)被认为是窄带信号。信号z(t)的带宽可表示为两部分之和,即![]() ,其中
,其中![]() 反映了信号的瞬时幅值a(t)的变化情况,只与幅值调制有关。
反映了信号的瞬时幅值a(t)的变化情况,只与幅值调制有关。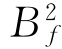 称为频率带宽,反映了信号的瞬时频率φ′(t)的变化情况,也反映了信号的瞬时频率在整个时间段内的聚集程度。
称为频率带宽,反映了信号的瞬时频率φ′(t)的变化情况,也反映了信号的瞬时频率在整个时间段内的聚集程度。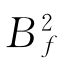 越小,说明信号的不同时刻的尺度特征越接近,尺度混淆越弱[111-114]。因此,
越小,说明信号的不同时刻的尺度特征越接近,尺度混淆越弱[111-114]。因此,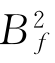 被用来作为GIMF的判别标准。
被用来作为GIMF的判别标准。
GIMF的定义是基于假设得到的pre-GIMFs,是近似窄带的,即如果z(t)=a(t)ejφ(t)是一个pre-GIMF,那么a(t)是带限信号,其最高频率远远小于φ′(t)。计算得到的每一个pre-GIMF的带宽Bi与中心频率ωi[]的比值,即![]() ,其中,i=1,2,…,P。那么具有最小γi的pre-GIMF分量将被视为最终的GIMF。详细的关于
,其中,i=1,2,…,P。那么具有最小γi的pre-GIMF分量将被视为最终的GIMF。详细的关于![]() 与ω[]的估计参见文献[111,112]。
与ω[]的估计参见文献[111,112]。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




