选择均值曲线的优化方法

EMD和LCD这类基于“筛分”的分解方法的关键是如何定义信号合理的均值曲线，然而到目前为止，EMD以及改进的EMD方法中，均值曲线的定义都是经验性的，还没有文献给出均值曲线的确切的数学定义。本章采用以下六种比较有代表性的均值曲线的定义方法。

（1）EMD中基于信号的上、下包络线定义的包络均值（envelop mean，EM）。

（2）固有时间尺度均值（intrinsic time-scale mean，ITM），定义方法参见Frei等提出的固有时间尺度分解。

（3）局部特征尺度均值（local characteristic-scale mean，LCM），定义方法参见本书第2章第3节。

（4）极值域均值（extrema field mean，EFM），定义方法参见盖强等提出的极值域均值分解[108]，步骤如下：

假设待分析信号为S（t）（t＞0），其所有的极值点记为（tk，Sk）（k=1，2，…，P，P是极值点数目），S（t）在区间[tk，tk+1]上的均值曲线可定义为

ti+1时刻的均值定义为(www.xing528.com)

（5）半波均值（half period mean，HPM）。

第（4）种方法中，由于S（t）在区间[tk，tk+1]上的均值曲线定义为mi（tξi），这里tξi近似等于，因此，采用三次样条函数对所有的（tξi，mi（tξi））进行插值即得到信号的另一种均值曲线。

（6）极值中值均值（extremum midpoint mean，EMM）。

假设待分析信号为Yt（t≥0），其所有极值点为（τk，Yk）（k=1，2，…，M），相邻两个极大（或极小）值的中点可表示为

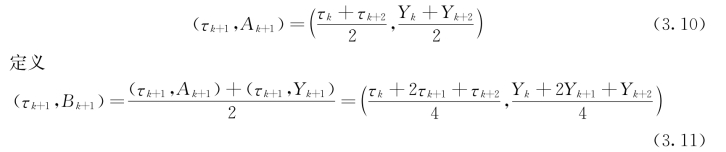
采用上述六种方法提取信号的均值曲线，事实上对应了六种信号的分解方法，而且每一种分解方法都有其不同的优势。如EMD的包络均值曲线（EM）能够有效地保证分解信号的对称性，对大部分信号而言，EMD方法仍有良好的分解性能。其不足之处在于，对极值点变化较大、分布不均匀的信号，由于采用三次样条插值，会产生包络过冲和不足，生成新的极值点，从而导致分解误差。ITM和LCM避开了包络线的定义方法，基于数据的特征尺度而定义，每一个极值点处的均值均采用相邻的三个极值点而定义，再分别采用基于数据本身的线性变换和三次样条插值定义均值曲线，因此能很好地反映信号的局部特征，提高分解频率分辨能力，但不足的是，二者对噪声较敏感，ITM易引起波形的失真，LCM易导致分量幅值一致化。EMM是为了克服LCM对相邻极值幅值变化较大从而造成均值点偏移而提出。EFM和HPM是基于相邻的两极值点间一段数据来定义均值点，更能反映数据的局部性特征，提高分解的频率分辨能力，但对调频较大的信号易出现均值不为零从而导致过度筛分。图3.13给出了一个信号的六种不同均值曲线。

给出三点注记。首先，由于理论限制，六种曲线的合理性和数学模型目前仍较难论证，但是不合理的均值曲线得到的分量将会被GEMD方法舍弃，不会影响分解的结果。其次，对于大部分瞬时频率和瞬时幅值为常函数或变化缓慢的调幅调频信号，上述六种均值曲线的差别不大，这是容易理解的，因为对常见的等单分量信号无论哪种方法求得的均值都应该趋于理论值零。再次，现有文献关于均值曲线的定义远不止六种，本文方法中只选取比较有代表性的六种。