EMD、LCD和ILCD对比分析

为了说明所提出的ILCD的优越性，不失一般地，考虑式（3.4）所示的混合信号x（t）：

其中x1（t）=[1+0.6sin（2π3t）]cos（2π50t+2π5t2），x2（t）=2cos（2π25t）。x1（t），x2（t）与x（t）的时域波形如图3.1所示。

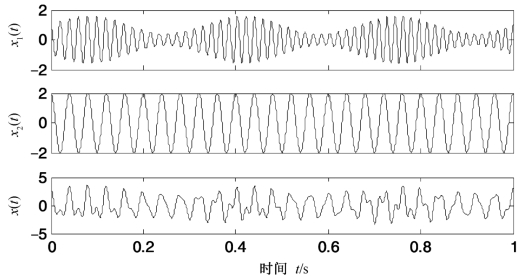
图3.1　式（3.4）所示混合信号和其各成分的时域波形

分别采用EMD、LCD和ILCD对x（t）进行分解，结果分别如图3.2～图3.4所示。其中，图3.2中c1，c2和r2分别表示第一和第二个IMF分量以及剩余项，图3.3和图3.4中I1，I2和r2分别表示第一和第二个ISC分量以及剩余项。为了方便比较，图3.5给出了三种分解方法的分解绝对误差，分解绝对误差定义为分解得到的分量与真实分量之差的绝对值，图中，E1和E2分别表示三种方法第一和第二个分量与真实分量x1（t）和x2（t）的绝对误差。

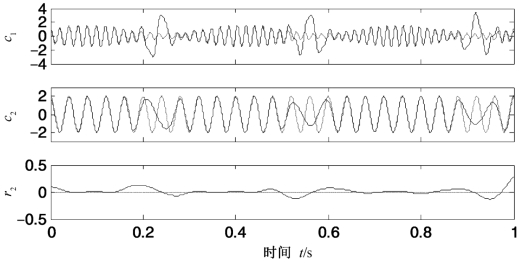
图3.2　式（3.4）所示混合信号的EMD分解结果

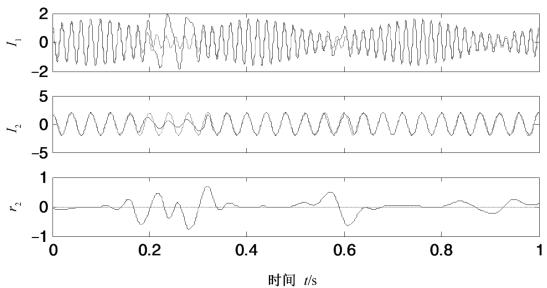
图3.3　式（3.4）所示混合信号的LCD分解结果

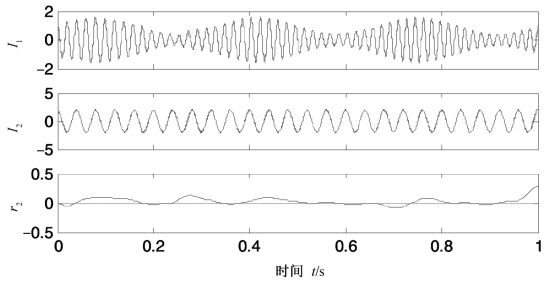
图3.4　式（3.4）所示混合信号的ILCD分解结果(www.xing528.com)

图3.5　式（3.4）所示混合信号三种分解方法的分解结果绝对误差

由图3.2～图3.5可以看出，EMD的分解结果中IMF分量c1与c2局部波形严重失真，与真实分量误差较大；LCD的分解结果中ISC分量I1与I2虽然波形局部失真情况不如EMD分解中IMF分量失真严重，但与真实分量误差幅值也比较大（从图3.5中可以明显看出）；与前两者相比，ILCD分解则比较理想，分解分量与真实分量非常接近，绝对误差幅值非常小。

为了进一步比较三种方法的分解效果，本文还考察了三种分解方法的分解正交性指标（index of orthogonality，IO），前两个分量的正交性指标以及三种分解方法前两个分量与真实分量绝对误差的能量。正交性指标越小说明分解正交性越好；绝对误差的能量越小，说明误差越小。其中，分解正交性指标[23，107]

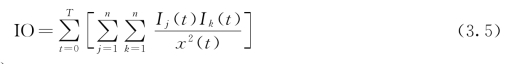
这里，为方便，记In（t）=un（t）。

两个单分量信号f（t），g（t）的正交性定义为

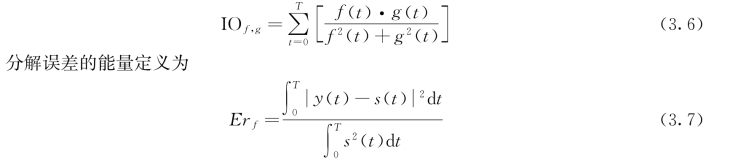
其中，y（t），s（t）分别为估计值和对应真实值。

上述三种分解方法的分解指标分别如表3.1所示，其中，IO表示分解结果正交性，IO12表示分解的第一个和第二个分量的正交性，Eri表示第i个分量与其对应真实分量的绝对误差的能量，i=1，2。由表中可以看出，与EMD和LCD方法相比，ILCD方法的正交性指标和误差能量指标都是最小的，这说明ILCD在正交性和精确性方面有一定的优越性。

表3.1　EMD，LCD和ILCD分解结果评价指标比较