数据传输差错控制技术详解

串行数据在传输过程中，由于干扰而引起误码是难免的，这将直接影响通信系统的可靠性，所以，通信中的差错控制能力是衡量一个通信系统的重要指标。我们把如何发现传输中的错误，叫检错；在发现错误之后，如何消除错误，叫纠错。在基本通信规程中一般采用奇偶校验或方阵码检错，在高级通信控制规程中一般采用循环冗余码CRC（Cyclic Redundancy Code）检错和自动纠错。

1.奇偶校验

在发送数据时，数据位尾随的1位为奇偶校验位（1或0）。奇校验时，数据中“1”的个数与校验位“1”的个数之和应为奇数；偶校验时，数据中“1”的个数与校验位“1”的个数之和应为偶数。接收字符时，对“1”的个数进行校验，若发现不一致，则说明传输数据过程中出现了差错。奇偶校验的缺陷在于若有2位（或偶数位）变化时，则检测不出差错。

2.方阵码检错

方阵码检错技术是奇偶校验与“检验和”的综合。例如，7位编码的字符附1位奇偶校验位，以使整个字节的“1”的个数为偶数或者为奇数。让若干个带检验位字符组成一个数据块，并对所有数据块中的字符纵向按位加，产生一个单字节的检验字符并附加到数据块末尾，如表5-2所示。这一检验字符实际是所有字节“异或”的结果，反映了整个数据块的奇偶性。在接收时，数据块读出产生一个检验字符和发送来的检验字符进行比较。如果两者不同，就表明有错码，反馈重发。

3.循环冗余码（CRC）检错和自动纠错(www.xing528.com)

CRC循环校验是数据通信领域中最常用的一种差错校验码，其特征是信息字段和校验字段的长度可以任意选定。对于任意一个由二进制位串组成的代码都可以和一个系数仅为“0”和“1”取值的多项式一一对应。例如：代码1010111对应的多项式为x6+x4+x2+x+1，而多项式为x5+x3+x2+x+1对应的代码101111。可见，n位二进制数，可以用n-1阶多项式表示。

表5-2　方阵码举例

CRC循环校验的原理是，对于一个长度为k位的二进制信息码元，其多项式用M（x）表示，发送装置将产生一个r位的码元序列，称为监督码序列，其用多项式R（x）表示。r位监督码附加在k位的信息码元序列后面，组成总长度为n位（n=k+r）的循环码序列，其多项式为C（x），并将n位的循环码作为一帧信息发送出去。这个n位的循环码序列可以被某个预定的生成多项式G（x）整除，接收装置对接收到的n位码元除以同样的生成多项式G（x），当无余数时，则认为没有错误。

CRC校验的要点是选择生成多项式G（x）和如何确定监督码R（x）的问题。首先选定作为除数的生成多项式G（x），其次将信息码多项式M（x）乘以xr再除以生成多项式G（x）得到余项R（x），最后得到循环码C（x）=M（x）xr+R（x）。

如信息字段代码为1011001，对应的多项式为M（x）=x6+x4+x3+1，假设生成多项式为G（x）=x4+x3+1，G（x）对应的代码为11001，则M（x）x4=x10+x8+x7+x4对应的代码记为10110010000。采用多项式除法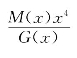得余数为1010，即校验字段为1010，发出的循环码为：1 0 1 1 0 0 1 1 0 10。