1.基于正弦函数模型的算法——半周积分算法
实际应用中，由于各种不对称因素及干扰的存在，电流和电压波形并不是理想的工频正弦波，而是存在高次谐波，尤其是在电力系统故障时，还会产生衰减直流分量。但一些较为简单的算法，考虑到交流输入回路中设有R-C滤波电路，为了减少计算量，加快计算速度，往往假设电流、电压为理想的正弦波。当然这样会带来误差，但只要误差在应用的允许范围内，也就是许可的。
半周积分算法的依据是一个正弦量在任意半个周期内绝对值的积分是一常数S，以正弦电流为例
积分值S与积分起始点的初相角α无关。如图3-20所示，积分的起始点无论从0或从α角开始，积分半周期的绝对值总是常数，因为图中画斜线的两块面积是相等的。
由式（3-3）看出，求出积分常数S即可求出正弦电流的有效值或幅值。在微机系统中，积分常数S用梯形法则转换成累加和近似求出。
式中 ik——第k次采样值，k取0、1、2、…、N/2；
N——1个工频周期的采样点数。
图3-20 半周积分算法原理
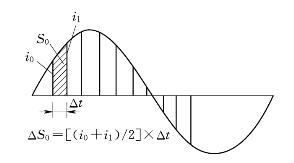
图3-21 梯形法近似计算积分面积示意图
只要采样点数N足够多，用梯形法近似求取积分的误差可以做到很小，如图3-21所示。半周期积分算法本身具有一定的高频分量滤除能力，因为叠加在基波上的高频分量在半周期积分中其对称的正负半周互相抵消，剩余的未被抵消部分占的比重就很小了。但这种算法不能抑制直流分量，可配一个简单的差分滤波器来抑制电流中的非周期分量（直流分量）。
2.基于周期函数模型的算法——傅氏变换算法
傅氏算法适用于周期变化的信号，即采样的模拟电压和电流除基波外还含有不衰减的直流分量和各次谐波。傅氏算法的基本思路来自傅里叶级数，以电压为例，用傅里叶级数可展开为
(www.xing528.com)
式中 U0——直流分量；
an、bn——各次谐波正弦项和余弦项的幅值。
若求出系数an和bn，则可求出各次谐波分量（包括基波）的有效值或幅值以及初相位。以基波为例
可根据a1和b1求出电压有效值和初相角
根据傅氏级数的原理，可求出a1和b1
用梯形法则转换成累加和为
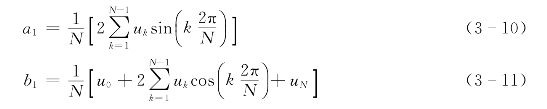
式中 N——一个工频周期采样点数；
uk——第k次采样值，k=0、1、2、…、N。
同理，对于n次谐波来说，an和bn用梯形法则近似求出
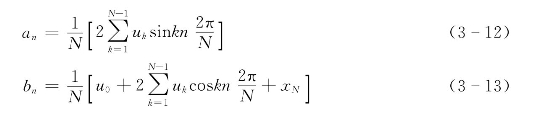
则n次谐波有效值和初相角为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
