水资源安全的层次分析综合评价方法

层次分析法运用系统分析思想把复杂的问题分成若干联系的、有序的层次,对每一层次的相关元素进行比较分析,一般情况下具有三个层次:总体层(或称目标层)、准则层(或称系统层)和指标层。若问题比较复杂,每层下还可细分为次要层次,以便更加深入分析问题。本研究涉及自然和社会经济复合系统的诸多子系统和因子,拟分3个层次:总体层、准则层和指标层,将指标体系的横向结构确立起来。

1.水资源安全评价指标体系

建立评价指标体系时,首先选取最能反映和度量被评价对象优劣程度的指标。本次研究坚持以生态平衡、安全平衡、力的作用与动态平衡为指导思想,通过(在第七章)详细的分析比较,本文建立的水资源安全指标体系见表12-13。

表12-13　水资源安全评价指标体系

指标体系包含1 个总体层 (A),7 个系统层 (B 1～B 7),共21 个指标(C1～C21)。准则层B 1至准则层B 6下的各项指标都是定量的客观指标,要全面准确地判断和评价水资源安全的形势,必须同时使用主观指标和客观指标,使用主观指标可以弥补客观指标的不足之处。作者又建立了定性指标社会管理力 (B7),包括法规制度、水价、公共权力、道德意识等政治和伦理道德因素。

收集山西省11个地市的各项指标,组成原始评价集。

2.数据标准化

由于各指标具体量纲不同,无法进行直接比较,为了消除各评价指标的量纲影响,需对各评价指标的原始数据进行标准化处理,数据标准化的方法有很多种,本文根据不同评价指标的属性,将评价指标划分为三种类型:效益型(越大越优型)、成本型(越小越优型)和中间型 (越中越优型),根据不同的指标类型选择不同的标准化公式进行处理。

对效益型指标

对成本型指标

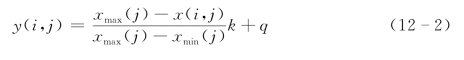
对中间型指标

式中 xmin(j)、xmax(j)、xmid(j)——第j个指标的最小值、最大值和中间理想值；

x(i,j)、y(i,j)——标准化前、后的评价指标值,处理后的数据在[q,k+q]范围内。

按以上算法,标准化处理后的值见表12-14。

3.建立判断矩阵, 赋权重

遵循层次分析原理,依据标度法(见表7-7),建立总体层与准则层的评判矩阵和各准则层与其指标的评判矩阵。

各结构层中的相对权重,采用方根法求解的归一化特征向量和特征值,直到满足一致性检验,所求特征向量就是各因子的权重排序

判断矩阵的一致性检验,A 判断矩阵满足性质:

表12-14　标准化后的评价矩阵

(1)aii=1(i=1,2,…,n)；

(2)aij=1/aji(i,j=1,2,…,n)；

(3)aij=aik/akj(i,j,k=1,2,…,n)。

其中(3)称为A 的完全一致性条件,即

式中 λ——A 的一个特征根；

W——A 对应于λ 的特征向量,W = (w1,w2,…,wn)T。

计算最大特征根

对判断矩阵进行一致性检验

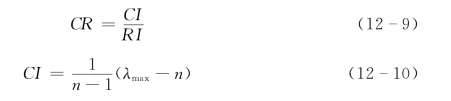
式中 CR——判断矩阵的随机一致性比率；

CI——判断矩阵的一般一致性指标；

RI——判断矩阵的平均随机一致性指标,RI取值见表7-8。

根据表7-8中RI值,计算评判矩阵的随机一致性比率CR,当判断矩阵的随机一致性比率CR＜0.1时,可认为该判断矩阵具有满意的一致性,各评价指标的权重值是可以接受的；否则,要修正判断矩阵,直到具有满意的一致性为止。

按照上述思想,应用层次分析法,通过专家评价,构造评价矩阵,水资源安全为总体目标A,相对于总体目标而言,七大目标B1～B 7之间的相对重要性,评价矩阵见表12-15,经计算,CR=0.053＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 具有满意的一致性。

表12-15　目标层A与准则层B评价矩阵

续表

注 λmax=7.4208 CI=0.0701 CR=0.053

水资源力准则层与其指标层的评价矩阵见表12-16,CR=0＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 1具有满意的一致性。(www.xing528.com)

表12-16　准则层B1与其指标层C评价矩阵

注 λmax=2 CI=0 CR=0

表12-17　准则层B2与其指标层C评价矩阵

注 λmax=2.0001 CI=0 CR=0

社会经济力与其指标层的评价矩阵见表12-17,CR=0＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 2具有满意的一致性。

开发利用力与其指标层的评价矩阵见表12-18,CR=0＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 3具有满意的一致性。

环境力与其指标层的评价矩阵见表12-19,CR=0＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 4具有满意的一致性。

表12-18　准则层B3与其指标层C评价矩阵

注 λmax=2 CI=0 CR=0

表12-19　准则层B4与其指标层C评价矩阵

注 λmax=2 CI=0 CR=0

再生力与其指标层的评价矩阵见表12-20,CR=0.017＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 5具有满意的一致性。

科技力与其指标层的评价矩阵见表12-21,CR=0.041＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 6具有满意的一致性。

社会管理力与其指标层的评价矩阵见表12-22,CR=0.079＜0.1,通过随机一致性比率检验,可以认为评价矩阵A 7具有满意的一致性。

表12-20　准则层B5与其指标层C评价矩阵

注 λmax=4.0456 CI=0.0152 CR=0.017

表12-21　准则层B6与其指标层C评价矩阵

注 λmax=5.1856 CI=0.0464 CR=0.041

表12-22　准则层B7与其指标层C评价矩阵

注 λmax=4.2148 CI=0.0716 CR=0.079

通过以上计算,得到子系统对目标层的权重和评价指标对子系统的权重,见表12-23。

表12-23　水资源安全评价指标体系权重值

续表

4.综合评价

根据标准化后的指标乘以各自的权重,然后分层加总,就可以得到水资源安全的综合评价值。上一层指标值由对应的下一层指标值及其权重计算得到,即

式中 ——上层指标值；

——下一层指标权向量值；

——下一层指标向量值。

逐层计算,便可得到水资源安全综合评价值。综合评价值与水资源安全呈正相关,得分越高,水资源安全形势越好,反之亦然。

通过计算,山西省各地市准则层各子系统评价值见表12-24,综合评价值和排名次序见表12-25。

根据综合排序相应的评价结果进行分析,可知得分由高到低的是晋城市、忻州市、长治市、临汾市、晋中市、阳泉市、吕梁地区、朔州市、运城市、太原市、大同市。得分最高的是晋城市,从各方面综合来评价,晋城市的水资源安全形势最乐观,得分最低的是大同市,大同市的水资源安全形势最不容乐观。

表12-24　各子系统评价值

表12-25　水资源安全综合评价值

为使评价结果合理可信,我们采用两种理论方法对水资源安全进行评价,以下应用Vague集理论对水资源安全综合评价进行研究。