突发性水资源安全风险的分析及应对策略

扩散方程的求解和污染源的存在形式密切有关。从污染源在水体空间的存在形式看,有瞬时源和时间连续源。瞬时源是指污染物质在瞬时内投放于水域,实际上这也是一种近似,如突然事故产生的核污染或者油轮事故突然泄放的油污染可近似看作瞬时污染源。本节就突发性水资源安全风险进行研究,把突发性的水资源安全问题近似看作瞬时污染源。

含有某一有毒物质在水体中的扩散按二维流来考虑,对大多数实际问题,水流具有明显的主流方向,其uy、uz可以忽略不计,二维扩散方程为式 (10-3),解析式为式(10-4)。

假如c表示一种在水里可以降解的污染物的浓度,它的衰减反应系数为k,则式(10-4)变为式(10-7)

河流某断面超标风险率定义为有毒物质在某一泄漏时间 (或时间段)之后,在河流中某断面超过该物质的水质标准的概率。即

当x=x0,t=t0

式中 B——河流宽。

如果f(x,y,t,c)已知,则通过式(10-8)积分,即可求得风险R。

如设

式(10-7)转化为

式 (10-9)是关于y 的标准正态分布函数,均值为0,均方差为σy,φ(y)为y服从N(0,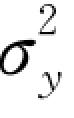)分布的密度函数。

由于河流断面某一点的实测浓度为(www.xing528.com)

式中 c*(x,y,t)——有毒物质在 (x,y)处,泄漏时间为t 时的实际浓度值。

在计算断面超标风险率时,对上式可进行以下简化:

(1)以c(x,y,t)代替c*(x,y,t)进行计算。

(2)假定计算所得c(x,y,t)小于c0时,该点超标风险率为零。从而有

当x=x0,t=t0

R 表示有毒物质在断面x0处,泄漏时间为t0时的超标风险率。

求出c(y)/c0=1时的y 值,根据函数φ(y)的对称性,其解有两个y1、y2,且y1=-y2,设y1＜y2。

计算x=x0,t=t0时的超标风险率

式中 F——标准正态分布变量累积分布函数。