【摘要】：在层流,因边界引起粘性剪切力的存在,这种均匀流动实际是难以遇到的。因此,这只是一种假想的流动,但对这种流动的扩散便于作理论分析,对有些实际紊流也可近似应用。图10-1微元扩散方程是在研究分子扩散理论的基础上得到的,在溶液中取出一微分六面体如图10-1所示。河流发生某一有毒物质泄漏的突发事故,有毒物质在河流中的扩散按均匀紊流中瞬时源扩散来研究。
在流动流体中物质的扩散应按移流扩散方程 (在紊流则为紊流扩散方程)分析,在复杂的流动情况求解是困难的,但在单向的均匀流动中,即各处流速均为ux、uy=uz=0的情况,就有一些解析解。在层流,因边界引起粘性剪切力的存在,这种均匀流动实际是难以遇到的。在紊流,严格说来也不可能出现,因没有剪切力就不能维持均匀紊流而不衰减。因此,这只是一种假想的流动,但对这种流动的扩散便于作理论分析,对有些实际紊流也可近似应用。
图10-1 微元
扩散方程是在研究分子扩散理论的基础上得到的,在溶液中取出一微分六面体如图10-1所示。
六面体的各边长分别为d x、d y、d z,中心点的坐标为 (x,y,z),浓度为c(x,y,z),ux、uy、uz为x、y、z 3个方向的流速。
河流发生某一有毒物质泄漏的突发事故,有毒物质在河流中的扩散按均匀紊流中瞬时源扩散来研究。
当不考虑边界影响时,对瞬时点源
式中 c——有毒物质的浓度；
t——有毒物质的泄漏时间；
ux、uy、uz——水流在x、y、z方向的速度分量；
∑S——内部所有源和汇的代数和,如流动内部没有扩散质的发生与衰减时,∑S=0。
其浓度解为
(www.xing528.com)
式中 M——溶质质量,kg；
其余符号意义同前。
瞬时(线)源的二维扩散方程为
浓度解为
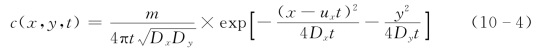
式中 m——单位长度包含的溶质质量,kg/m；
Dx、Dy——x、y 方向的弥散系数；
其余符号意义同前。
瞬时(面)源的一维扩散方程为
浓度解为
式中 μ——单位面积包含的溶质质量,kg/m2；
其余符号意义同前。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
