基本原理：水资源安全控制

水资源安全系统是一开放复杂的巨系统,因此对于水资源安全控制可采用大系统控制理论。在大系统模型化方面,大系统理论继承了控制理论和运筹学中的模型化方法,主要采用数学模型为

式中 x1,x2,…,xn——状态变量；

n——正整数；

u1,u2,…,ur——控制变量；

r——正整数,r≤n；

a11,a12,…,ann——常系数；

b11,b12,…,bnr——常系数。

若用矩阵形式表示,则可写成

式中 x——状态矢量,n维,x= (x1,x2,…xn)T；

u——控制矢量,r维,u= (u1,u2,…ur)T；

A——对象(系统)矩阵；

B——控制矩阵；

T——矢量转置。

因此,在状态空间Rn中某一点,相应于某一状态矢量x= (x1,x2,…,xn)T。

为了实现系统的有目的的状态转移,需要对系统进行控制,施加控制作用。例如,水资源安全系统的用水问题,为了提高系统的安全性,减少水资源的浪费,提高用水效率,需要对安全系统的用水问题进行科学合理控制,施加所需的控制信号或控制作用。可用控制矢量表示控制作用

式中 u——控制矢量,r维,通常r≤n；

uj——控制变量(标量),j=1,2,…,r。

利用状态矢量和控制矢量,可构成如下的三元组

式中 xs——初始状态矢量,xs= (x1s,x2s,…,xns)T；

xg——目标状态矢量,xg= (x1g,x2g,…,xng)T；

u——控制变量,u= (u1,u2,…,ur)T；

F(u)——由u 产生的状态转移操作。

三元组式(9-4)即空间状态空间模型。它描述系统从初始状态xs转移至目标状态xg的控制过程。

从行动规则看:

xs表示系统初始位置；xg表示系统目标位置；u 表示控制作用。

从模式识别看:

xs表示输入模式(控制数据等)；xg表示输出模式；u 表示识别操作 (特征抽取、模式匹配等)。

从故障诊断或疾病诊断看:

xs表示故障现象或疾病症状,例如工业用水浪费问题、工业结构不合理问题、地下水超采问题、水资源的质量问题等；xg表示诊断结论,比如通过故障诊断,某一区域的水资源安全问题是产业结构不合理等；u 表示诊断推理。

从博弈看:

水资源安全系统运行健康与否,实际上就是我们在第七章描述那样,是作用力与反作用力斗争的结果,是水资源力、再生力、环境力等与开发力、利用力等斗争的结果。所以,xs表示例局(初始博弈状态)；xg表示终局 (终止博弈状态)；u 表示博弈策略。

从逻辑证明看:

xs表示已知条件；xg表示求证结果；u 表示演算证明。

从管理看:

xs表示原始资料(目标、条件、信息、数据)；xg表示决策方案；u 表示决策分析与制定。

如果从纯粹控制论的角度看,在状态空间表达法的“三元组”模型中,控制矢量或操作矢量u= (u1,u2,…,ur)T是广义的。例如,u 可以是定型的推理步骤(例如安全诊断),定量的演算方法(例如定理证明、优化计算),静态操作序列,动态的控制变量(例如状态控制与调节作用)。

要保障水资源安全系统的正常、健康、良性的运行,除了其本身的自组织外,必须要对其系统进行科学的合理调节与控制。在现代控制理论中,主要采用“状态方程”作为被控制对象的数学模型,描述在控制变量作用下,被控制对象状态变化的动态过程。

通常,状态方程是指包含状态变量和控制变量的微分方程组,其一般形式是非线性、变系数,一阶常微分方程组

式中 xi——状态变量,i=1,2,…,n；(www.xing528.com)

n——有限正整数；

uj——控制变量,j=1,2,…,r,r≤n；

fi——非线性函数,i=1,2,…,n；

t——自变量。

在函数f1,f2,…,fn中包含某些时变系数。

假设在某一时段,水资源安全系统是一线性定常系统,其状态方程为线性常系数一阶微分方程组

式中 aij——常系数；i=1,2,…,n；j=1,2,…,n；

bij——常系数,i=1,2,…,n；j=1,2,…,r。

线性系统的状态方程可写成矩阵形式

式中 x——状态变量,x= (x1,x2,…,xn)T；

u——控制矢量,u= (u1,u2,…,ur)T；

A——对象(系统)矩阵(描述被控制对象特性)

B 为控制矩阵(描述控制机构特性)

状态方程式(9-7)描述了被控制对象在控制作用下的状态变化过程,可称水资源安全系统的动态状态方程。

水资源安全系统的状态方程模型具有几种不同的变形,用以描述不同条件和情况下的系统状态及其变化过程。

1.水资源安全系统的静态状态方程

若动态状态方程式(9-7)中,令即水资源安全系统状态x(t)不随时间t而变化,处于静态,可得描述该系统稳态关系的静态状态方程

2.水资源安全的自由状态方程

水资源安全系统处于自由状态,没有给被控制对象施加控制作用,即u=0,则由式(9-7)可得自由状态方程

3.水资源安全的输出状态方程

由于实际系统的状态˙x 并不一定都是可观测的输出y,设描述状态与输出的关系方程为

式中 y——输出矢量,y= (y1,y2,…,ym)T,m≤n；

C——观测矩阵(描述观测装置特性)。

由式(9-7)、式(9-12)及式(9-13)可得输出状态方程

4.水资源安全的输出控制方程

系统的控制作用u 不仅可以通过改变状态x 而影响输出y,而且可以直接对输出产生影响,即对输出的直接控制作用。

在这种情况下,描述系统的输出、状态、控制和静态关系的输出控制方程如下

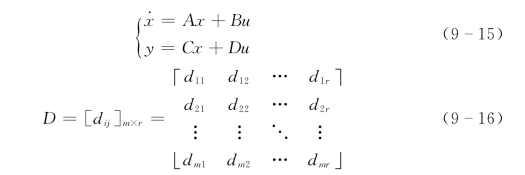
式中 D——直控矩阵(描述对输出的直接控制作用)。

式(9-15)是水资源安全(线性)系统状态方程模型的一般形式。

根据状态方程模式式(9-15),可以绘出相应原理图,如图9-2所示。利用上述各种形式的状态方程模型及控制系统原理图可进行水资源安全系统控制的动态、静态、定量、定性的分析与总和。

图9-2　水资源安全控制系统原理图

∫—积分符号 (微分符号 的逆运算)；
A—对象 (系统)矩阵 (被控制对象特性)；B—控制矩阵 (控制机构特性)；C—观测矩阵 (观测装置特性)；D—直接矩阵 (直接控制特性)