1.相对比较法
相对比较法的过程如下:将所有的评价指标Xj(j=1,2,…,n)分别按行和列排列,构成一个正方形的表;再根据三级比例标度对任意两个指标的相对重要关系进行分析,并将评分值记入表中相应的位置;将各个指标评分值按行求和,得到各个指标的评分总和;最后做归一化处理,求得指标的权重系数。
三级比例标度两两相对比较评分的分值为qij,则标度值及其含义如下

则评分构成的矩阵Q= (qij)n×n。显然,qij=0.5,qij+qji=1。指标Xi的权重系数为

使用该方法确定指标权重时,任意两个指标之间的相对重要程度要有可比性。这种可比性在主观判断评分时,应满足比较的传递性,即X1比X2重要,X2比X3重要,则X1比X3重要。
2.连环比率法
连环比率法也称作A.J.Klee (柯隶)法,采用这种方法确定指标权重,是将X1,X2,…,Xn等n 个指标以任意顺序排列,从前到后,依次赋以相邻两个指标相对重要性比率λi,然后根据最后一个指标的修正评分值计算各个指标的修正评分值,做归一化处理求出各个指标的权重系数值ωj。比率值λi以三级标度赋值如下

连环比率法的计算步骤为:①将评价指标以任意顺序排列;②从评价指标的上方依次以其邻近的下方指标为基础在数量上进行重要度的判断 (λj列);③把最下一指标的基准值定为1,从下至上顺序对各指标的λj值进行基准化,得σj值,即σj=λjσj+1(j=1,2,…,n-1);④将σj值进行归一化得ωj,即

3.PATTERN 法
PATTERN 法是一种关联树法,它是哈奈沃尔公司开发的,特别适合于确定从属层的权重计算。其计算步骤为:①将评价指标层 (目的属性层)排列成树形图,并选定评价基准项目;②在树形图的各水平上,为了评价其重要性,要设立每个水平的基准项目,要求各基准项目的权数和为1;③将属于此水平的各个分项目 (从属层指标)的权数包括基准在内合计定为1;④分别求出各项目的权与相应基准权之积,然后相加,得各项目的重要度。
4.专家咨询法
专家咨询法,又称特尔菲法,即组织若干对评价系统熟悉的专家,通过一定方式对指标权重独立地发表见解,并用统计方法做适当处理。
第一步,组织r个专家,对每个指标Xj(j=1,2,…,n)的权重进行估计,得到指标权重估计值W= (ωk1,ωk2,…,ωkn),(k=1,2,…,r);

第四步,对于偏差Δkj较大的第j 指标权重估计值,再请第k 个专家重新估计ωkj,经过几轮反复,直到偏差满足一定的要求为止,最后得到一组指标权重的平均估计修正值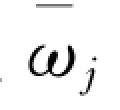 (j=1,2,…,n)。
(j=1,2,…,n)。
5.集值迭代法
采用集值迭代法确定指标权重的过程为:
第一步,选取L (L≥1)位专家,让每一位专家在指标集X=Xj(j=1,2,…,n)中任意选取其认为最重要的s (1≤s≤n)个指标,即第k (1≤k≤L)位专家选取的结果是指标集X 的一个子集X k= {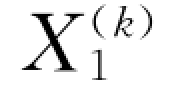 ,
, ,…,
,…,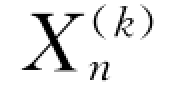 ) (k=1,2,…,L)。
) (k=1,2,…,L)。
第二步,作(示性)函数μk(j)
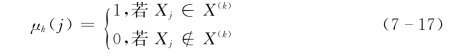
令
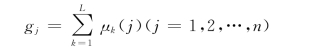
第三步,确定各个指标权重ωj

6.最小平方法和特征向量法
最小平方法首先将n个评价指标关于某个评价目标的重要程度按表7-7所列的比例标度做两两比较判断获得矩阵A。
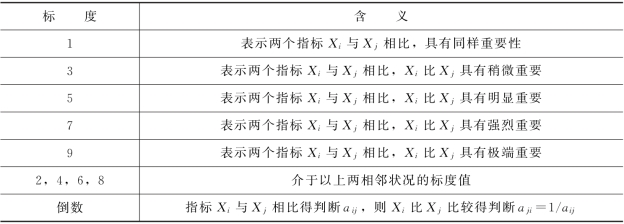
表7-7 1~9标度法
这种方法把目标的重要性做成对比较时,如果目标有n个,则共需要比较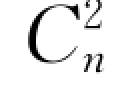 =n (n-1)/2次。把第i目标相对第j 目标的相对重要性的估计值记为aij,并近似地认为这就是属性i的权ωi和属性j 的权ωj的比ωi/ωj。n 个目标成对比较的结果用矩阵A 表示,得到
=n (n-1)/2次。把第i目标相对第j 目标的相对重要性的估计值记为aij,并近似地认为这就是属性i的权ωi和属性j 的权ωj的比ωi/ωj。n 个目标成对比较的结果用矩阵A 表示,得到
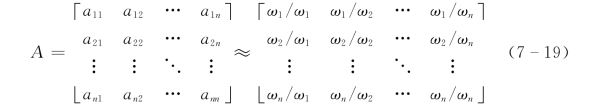
如果决策人对aij(i,j=1,2,…,n)的估计一致,则有

此外,决策人总会估计出aii=1,如果决策人对这些值aij的估计不一致,则只有
![]()
上式中的符号“≈”表示左右两侧近似相等,因此一般aijωj-ωi的值并不为0,但可以选择一组权{ω1,ω2,…,ωn},使其误差平方和最小,即(https://www.xing528.com)
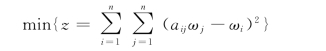
上式中的权{ω1,ω2,…,ωn}受约束于
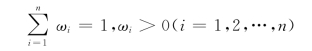
如用拉格朗日乘子法解此有约束的纯量优化问题,则拉格朗日函数为
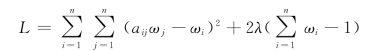
将上式对ω 微分,得到
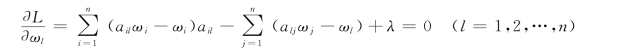
上两式构成了n+1 个非齐次线性方程组,有n+1 个未知数λ1,ω1,ω2,…,ωn,可以求得一组惟一的解。
7.层次分析法
层次分析法简称AHP法 (Analytical Hierarchy Process),是由美国运筹学专家T.L.Saaty于20世纪70年代中期提出的决策方法,基本过程是:首先将复杂问题分解成递阶层次结构,然后将下一层次的各因素相对于上一层次的各因素进行两两比较判断,构造判断矩阵,通过对判断矩阵的计算,进行层次的排序和一致性检验,最后进行层次总排序,得到各因素的组合权重,并通过排序结果分析和解决问题。这种方法具有需求的信息量很少,决策过程花费的时间短等特点。
运用层次分析法确定权重,可以分为以下几个步骤:
第一步,建立递阶层次结构。首先把问题条理化、层次化,构造出一个层次分析的结构模型。同一层元素对下一层的某些元素起支配作用,同时它又受上一层次元素的支配。每一层次中各元素所支配的下一层次元素一般最好不要超过9个,否则将会给两两比较判断带来困难。一个好的层次结构对于解决问题是极为重要的,因而层次模型必须建立在深入分析的基础上。
第二步,构造判断矩阵。对递阶层次结构中各层上的元素可以依次相对与之有关的上一层元素进行两两比较,建立判断矩阵。判断矩阵具有下述性质
![]()
式中,aij(i,j=1,2,…,n)代表元素Xi与Xj相对于其上一层元素重要性的比例标度。判断矩阵的值直接反映了人们对各因素的相对重要性的认识,一般采用1~9比例标度对重要性程度赋值,标度及其含义如表7-7所示。
第三步,计算单一准则下元素的相对权重并进行一致性检验。
设判断矩阵A 的最大特征根为λmax,其相应的特征向量为W,将W 归一化后即为同一层次相应元素对于上一层次某一元素相对重要性的权重问题。
由于客观事物的复杂性以及人们对事物认识的模糊性和多样性,所给出的判断矩阵不可能完全保持一致,有必要进行一致性检验,计算一致性检验指标CI

式中 n——判断矩阵阶数。
若随机一致性比率CR=CI/RI<0.10,则判断矩阵具有满意的一致性,否则需要调整判断矩阵的元素取值。随机一致性指标取值见表7-8。
表7-8 RI取值

8.相容矩阵分析法
层次分析法和最小平方和法需要对判断矩阵A 进行一致性检验,而相容矩阵分析法,不仅能减少因反复重新构造判断矩阵的工作量,而且能保证判断矩阵的一致性,从而简化确定指标权重的过程。
设对任意判断矩阵A 进行迭代,当m=1,2,…,恒有
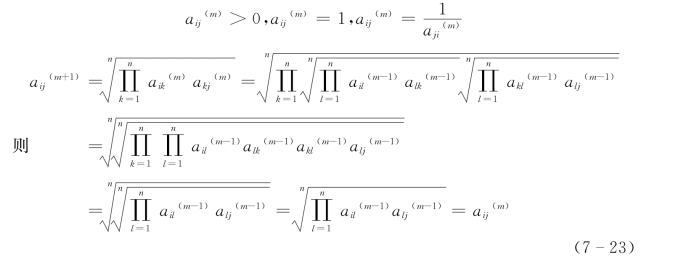
依次类推,得到
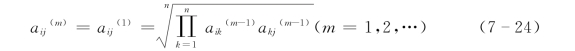
因而迭代极限存在
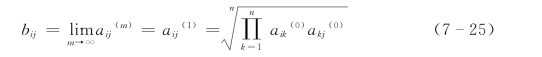
由此可得,任何一个矩阵A= (aij)经过一次迭代后变换为相容矩阵B=(bij),能满足一致性条件bij=bikbkj。因此,为确定指标权重提供了一个行之有效的方法,即相容矩阵分析法。
相容矩阵分析法的基本思路是将判断矩阵A= (aij)中的元素aij进行修正,使其成为满足一致性条件的判断矩阵。其计算步骤为:

![]()
第三步,求指标权重ωj
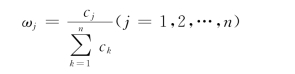
其中
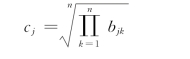
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




