保障水资源安全的平衡性

平衡性问题是水资源安全的中心问题,平衡不存在,那么水资源安全就会不存在,水资源就不安全,所以平衡问题是水资源安全问题的基本。从上面分析看出,水资源平衡性的描述就是对“人”作用下水资源系统的弹性范围的状态变化分析,也就是说对于水资源安全系统的平衡性描述,就是分析在 “人”的作用下水资源可利用量范围的水资源系统变化状态。我们可以认为,在“人”作用力不超过水资源系统的弹性范围情况下,水资源系统内任意点,以及边界点均处于平衡状态,点处于平衡,那么整个系统就处于平衡状态[这里有个问题:系统处于平衡状态,而点处于非平衡状态,这说明系统内的作用力是不一致的,是非均匀的。这在复杂的水资源系统是经常与事实存在的。这好像违背我们在分析水资源安全性的理想弹塑性体的假设,事实上没有违背我们的假设,这就是水资源安全分析的范围,是一个区域,一个流域,一个省,一个县,还是一个点,比如说我们描述一个区域的水资源安全状态,从区域看多年平均降水量为1712亿m3,地表水资源量216亿m3,地下水资源量235亿m3,水资源总量370亿m3；地表水资源可利用量158亿m3,地下水可利用资源量182亿m3,水资源可利用总量301亿m3；2000年该区域的地表水资源利用量为97亿m3,地下水资源利用量为193亿m3,水资源利用总量为290亿m3；水资源的开发率为地表水44.9%,地下水82.1%,总的78.3%；水资源的利用率为地表水61.4%,地下水106%,总的96.3%。因此,我们看出对地下水系统的安全状态已经进入塑性变形范围,但该区域水资源总的安全状态在水资源系统的弹性范围之内,在这一分析层次或分析范围(为了分析方便),我们可以认为此时的水资源安全系统的各个点均处于平衡状态。但这不能说我们忽视了地下水系统安全对整个区域水资源安全的作用,因为我们分析的水资源主要包括地表水资源与地下水资源,所以地下水资源安全状况或变化无时无刻不在影响着区域水资源安全的变化,只是分析的层次不同而描述的不同。这里也给我们提出另一个问题:区域水资源总的处于弹性状态,而地下水反之,这就要求我们利用地表余水通过地下水回灌等措施提高地下水的弹性能力]。

1.水资源安全系统的平衡微分方程

在弹性体内任一点P,如图6-5所示,取一微分平行六面体,如图6-6所示,其3条棱的长为d x、d y、d z。用X、Y、Z 代表单位体积的体积力在3个坐标方向的分量。由于所取的微分体是微小的,因而可以近似地认为体积力和各面作用应力是均匀分布的,系统弹性体内各面应力分量的大小及正方向如图6-6所示。由x、y、z向平衡,可得

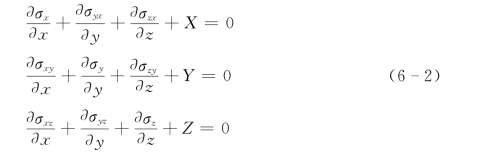
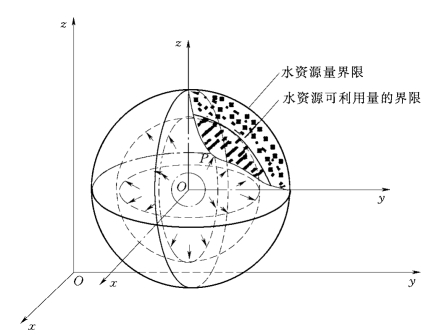
图6-5　水资源安全系统三维图

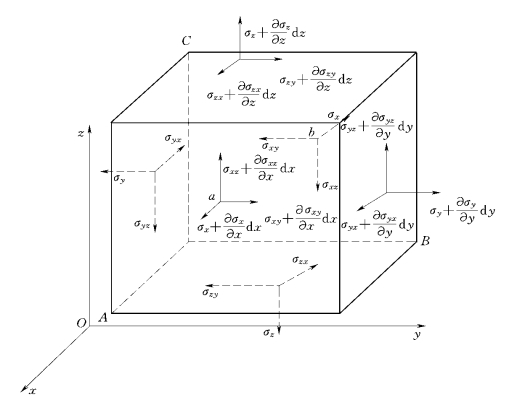
图6-6　水资源安全系统作用力平衡分析图

由对应面中心连线的作用力、力矩平衡,可得

2.作用力的平衡边界条件

用坐标面切割系统弹性体,在边界上一般得到的是微分四面体,如图6-7所示。记边界点单位面积上面力的3个分量为X、Y、Z,物体表面外法线的方向数为l、m、n,则由x、y、z向的平衡条件,可得

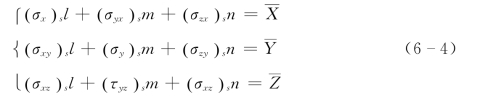
由力矩平衡条件,有(www.xing528.com)

式(6-4)为水资源系统空间问题的作用力的边界平衡条件。

假设水资源安全系统为一球体,若设取球坐标 (r,θ,φ)。我们从物体中切割出一微元体,如图6-8所示。

则

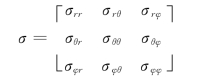
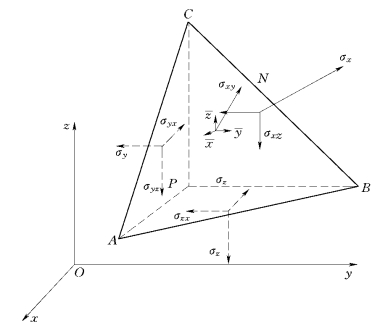
图6-7　水资源安全系统作用力边界平衡分析图

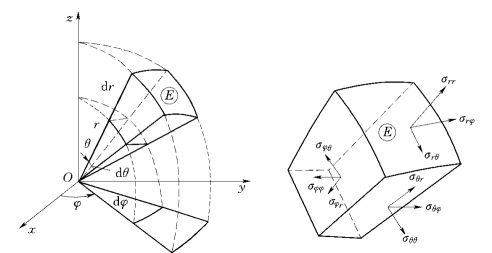
图6-8　水资源系统安全平衡分析图(球体)

或

设在球坐标系中的体积力f 的分量为 (fr,fθ,fφ),则水资源系统安全的平衡(运动)微分方程为

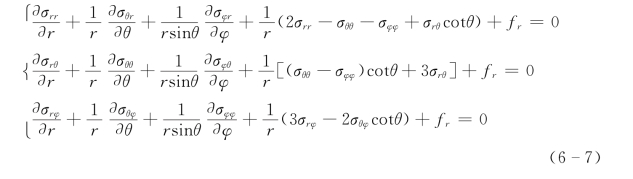
总之,水资源系统在“人”的作用下会发生运动和 “变形”,产生影响水资源安全的问题,并伴随水资源系统自组织作用而产生阻止系统变形的内力。显然,这种内力是作用在已变形系统上的。按照这种观点,水资源系统安全的平衡方程以及力的边界条件应该适用于已变形系统。因为我们现在分析的是水资源系统的安全状态,即外力作用下的水资源系统的弹性问题,可以讲是属于无限小变形理论或小变形理论,这时所有的应力分量都是同级量时。因此,建立在未变形系统和已变形系统上的平衡(运动)微分方程和力的边界条件具有相同的形式。如果放弃或部分放弃小变形的假设,即考虑弹性体的有限变形时,那就是弹性问题的有限变形的非线性问题,通过简化也是服从上述的水资源系统安全的平衡条件。