例2锥齿轮减速器主动轴由一对反装的30208圆锥滚子轴承支承(图2-16a),已知:.m=3.6mm,.=20,.=1450r/min,齿轮受力.t=2000N,.R=600N,.A=300N,载荷系数.d=1.2,静载安全系数.0=1.2。工作温度小于100.C。要求滚动轴承使用寿命不低于24000h。试问此滚动轴承是否能满足要求。
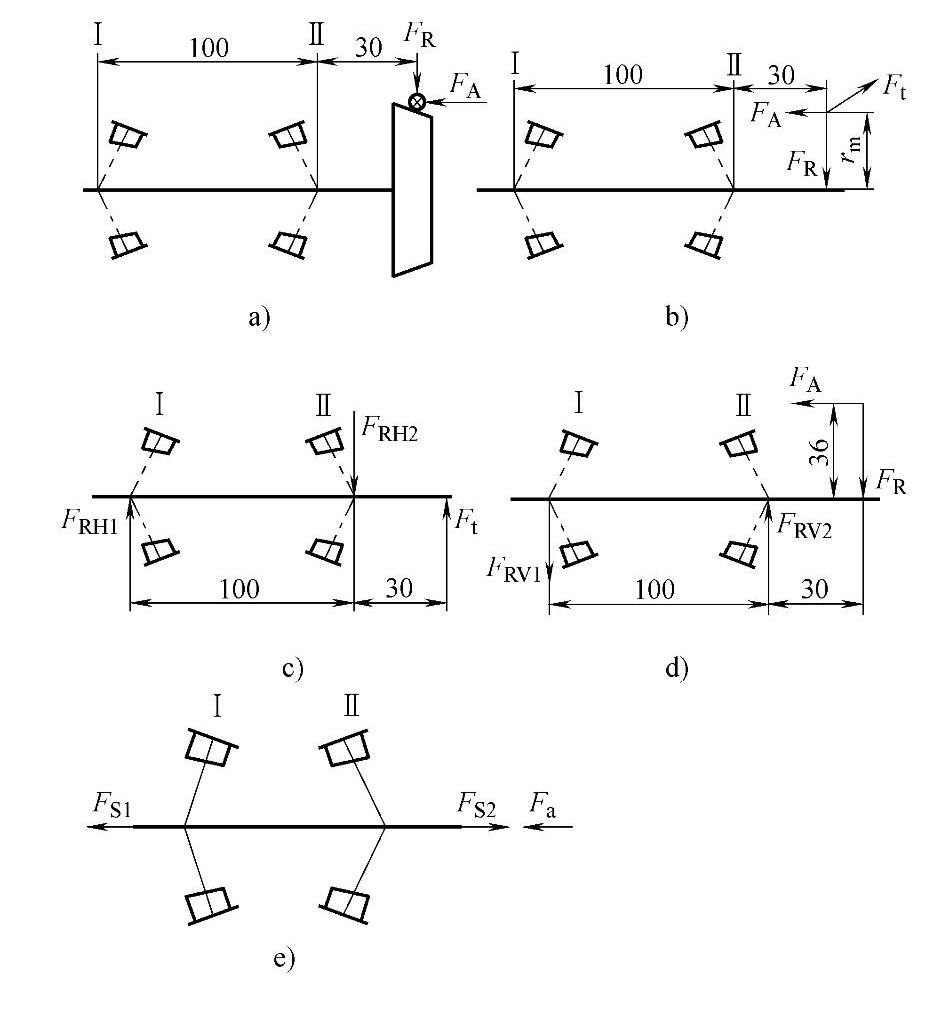
图2-16 例2图
解 查表2-21,得30208轴承额定动载荷.=63.0kN,额定静载荷.0=74.0kN,轴承几何尺寸.=18mm,.=18mm,故考虑压力中心后滚动轴承支点距离为100mm,锥齿轮悬臂伸出距离为30mm。系数.=0.37,.=1.6,.0=0.9。
(1)求轴承上径向载荷
锥齿轮平均半径.m(图2-16b)为
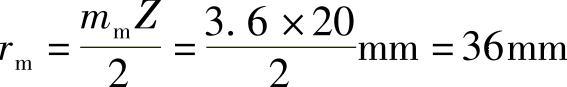
水平面支反力(图2-16c)为
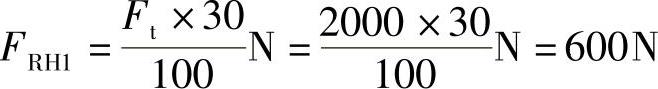
. RH2=.t+.RH1=(2000+600)N=2600N
垂直面支反力(图2-16d)为
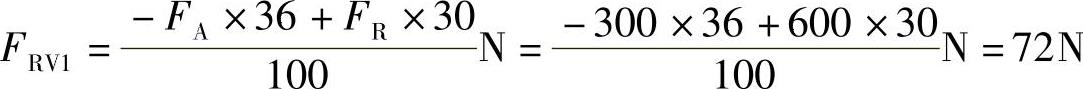
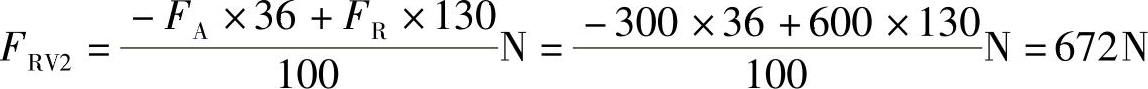
轴承的径向支反力为
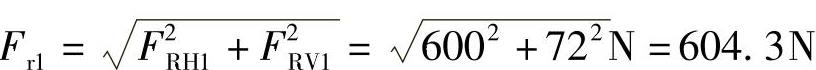
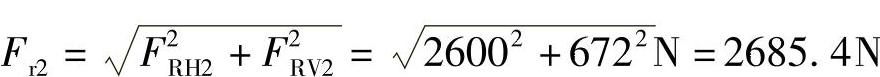
(2)求轴承的轴向支反力
①首先查表2-28,轴承类型为圆锥滚子轴承,确定内部轴向力(图2-16e)。
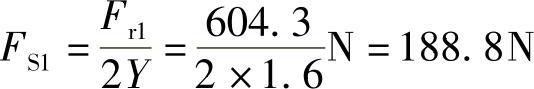
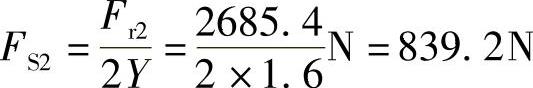
②判断轴上轴向力的方向。
. a+.S1=(300+188.8)N=488.8N﹤.S2=839.2N
③确定轴承压紧放松:轴承Ⅰ被压紧,轴承Ⅱ被放松。
④轴承的轴向载荷。
轴承Ⅰ被压紧,轴向载荷是除了自己产生的内部轴向力以外的轴上所有轴向力的合力,所以.a1=.S2-.a=(839.2-300)N=539.2N。
轴承Ⅱ被放松,则轴向载荷等于自己产生的内部轴向力,所以.a2=.S2=839.2N。
(3)求当量动载荷
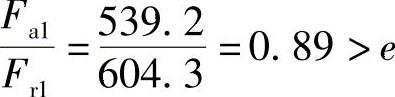
查表2-21,得.1=0.4,.1=1.6。
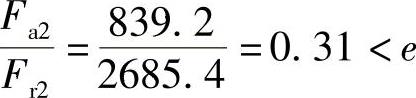
查表2-21,得.2=1,.2=0。
. 1=.d(.1.r1+.1 .a1)=1.2×(0.4×604.3+1.6×539.2)N=1325.3N
. 2=.d.r2=1.2×2685.4N=3222.5N
(4)校核轴承寿命 由上面计算可知.2﹥.1,故轴承Ⅱ危险,故校核轴承Ⅱ即可。

所以满足寿命要求。
(5)校核静强度查表2-21,得Xo=0.5,Yo=0.9,代人公式得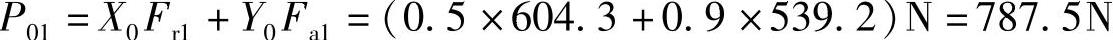
P01>Fr1,所以取P01=787.5N;用同样方法可求得
P02=Fr2=2685.4N
因为P02>P01,故轴承Ⅱ危险,故校核轴承Ⅱ即可。
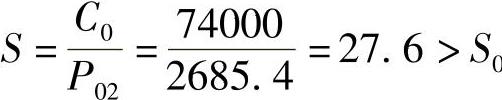
满足静强度要求。
例3 已知一蜗杆传动参数为m=10mm,q=8,Z1=2,Z2=41,n1=1440r/min。蜗杆受力为F1=837N,Fr=1066N,Fa=2928N,方向如图2-17a所示。蜗杆轴左端采用一对7209C轴承双向固定,右端选用6209轴承作游动支承,若要求寿命L10h>10000h,静载荷安全系数S。≥1.2,载荷系数.fd=1.2,试校核轴承是否满足要求,如有不满足者,试另选合适的轴承。
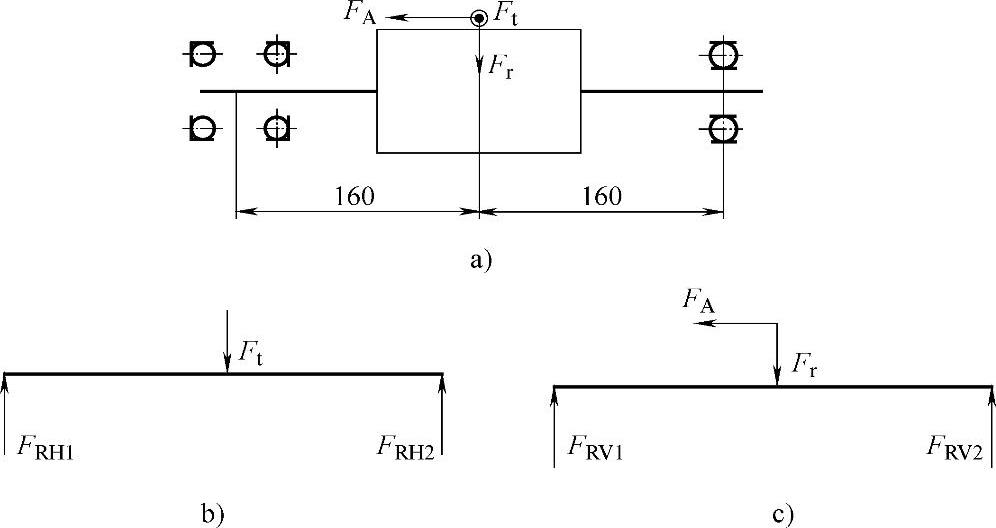
图2-17 例3图
解
(1)求轴承支反力

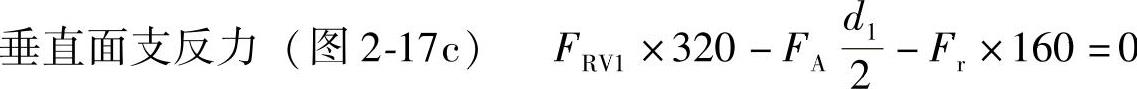
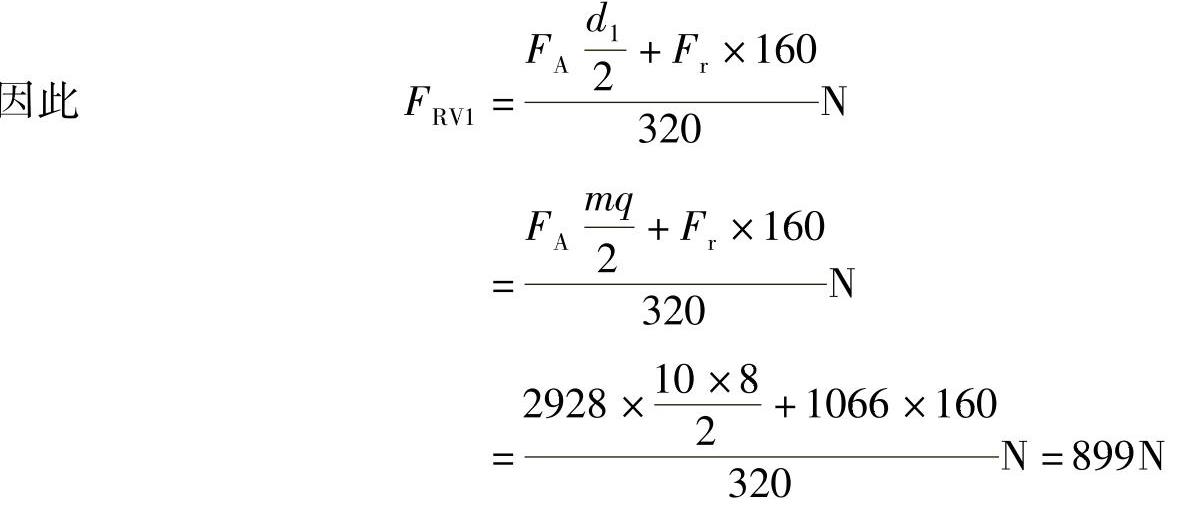
. RV2=.r-.RV1=(1066-899)N=167N
轴承的径向支反力为
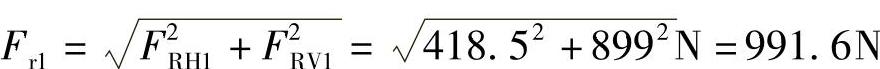
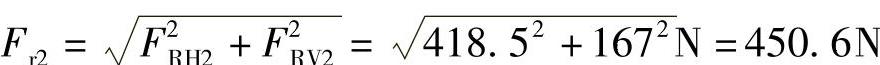
此题为一端固定、一端游动的支承方式,求轴承轴向支反力时,可将固定端的两个轴承看成一个双列轴承,全部轴向力由其承受,因此,轴承的轴向支反力为
. a1=.A=2928N
. a2=0(游动端不受轴向力)
(2)校核游动端轴承
查表2-27,载荷属轻微冲击,.d=1.2,所以
. 2=.d.r2=1.2×450.6N=540.7N
查表2-18,得6209轴承的.=31.5kN,.0=20.5kN
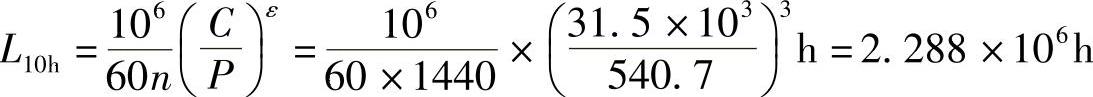
满足要求。
静强度校核
. 0=.r2=450.6N
由题目给出.0≥1.2,取.0=1.2,则
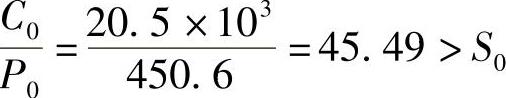
说明静强度足够。
由以上可知:游动端6209轴承的强度足够。
(3)校核固定端轴承
按一个双列角接触球轴承来考虑,则查表2-20,得7209C轴承的.=38.5kN,
. 0=28.5kN,因此
.Σ=1.625.=1.625×38.5×103N=62.56×103N
. 0Σ=2.0=2×28.5×103N=57×103 N
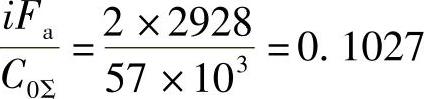
查表2-23b,当量动载荷计算中的 ,对此两行进行线性插值,即(.1=0.087,.1=0.46)、(.=0.1027,.)、(.2=0.12,.2=0.47)三点共线,
,对此两行进行线性插值,即(.1=0.087,.1=0.46)、(.=0.1027,.)、(.2=0.12,.2=0.47)三点共线,
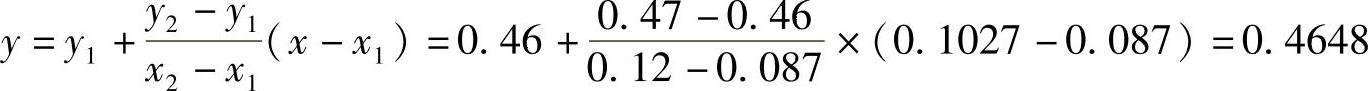
求得.=0.4648。
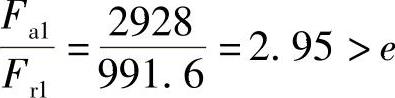
查表2-23b(或者表2-20)得:接触角为15.的双列角接触球轴承,.=0.72,.=1.97(用线性插值法求得),因此
. 1=.d(XFr1+YFa1)=1.2×(0.72×991.6+1.97×2928)N=7778.5N
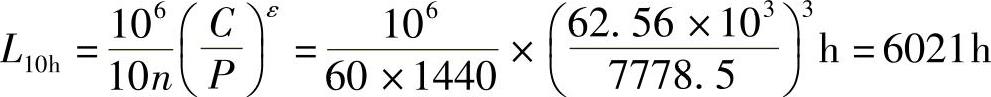
题目要求大于10000h,因此7209C轴承不满足使用要求,需另选其他轴承。
(4)改选一对7309B轴承校核
查手册7309B轴承的.=59.5kN,.0=39.8kN,因此(https://www.xing528.com)
.Σ=1.625.=1.625×59.5kN=97.6kN
. 0Σ=2.0=2×39.8kN=79.6kN
查表2-23b中公称接触角为40.的一行,得.=1.14,则
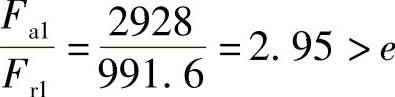
查表2-23b,.=0.57,.=0.93,因此
. 1=.d(XFr1+YFa1)=1.2×(0.57×991.6+0.93×2928)N=3945.9N
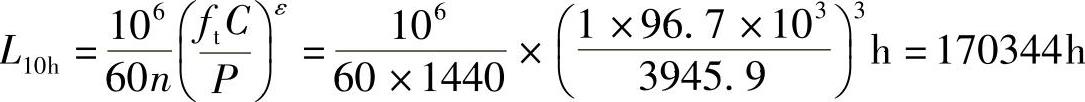
满足题目要求的10000h寿命,因此选7309B轴承合适。
查表2-26,得.0=1,.0=0.52,因此
. 01=.0.r1+.0.a1=(1×991.6+0.52×2928)N=2514N
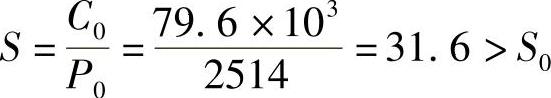
说明静强度足够。因此,固定端采用一对7309B轴承能满足使用要求。
本题也可按另一种方法解,即将固定端两轴承不视为一双列轴承,而看做两个轴承,支反力作用点按两个轴承中点计,先求出总径向支反力,再除以1.7(本应除以2,考虑到载荷并不完全均匀作用于两轴承,因此进行折算)即为每个轴承的径向支反力F′r1、F′r2;而求轴承的轴向支反力时,和一般求法相同,即将每个轴承的内部轴向力.S和外部轴向载荷同时考虑,判断压紧、放松端之后求出.a1、.a2。具体解法如下(图2-18):
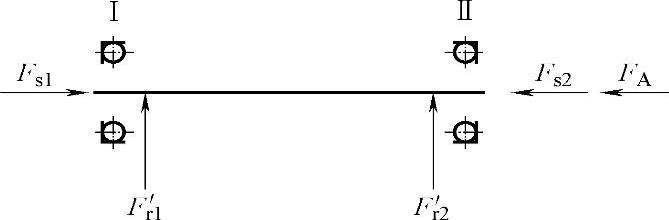
图2-18 例3解法二简图
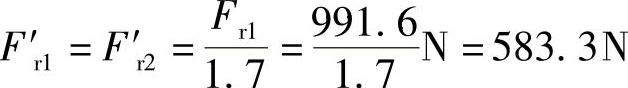
. S1=0.4F′r1=0.4×583.3N=233.3N
. S2=0.4F′r2=0.4×583.3N=233.3N
因为.A+.S2>.S1,因此轴承Ⅰ被压紧,轴承Ⅱ被放松,则
F′a1=.A+.S2=(2928+233.3)N=3161.3N
F′a2=.S2=233.3N
校核固定端,选7209C轴承。
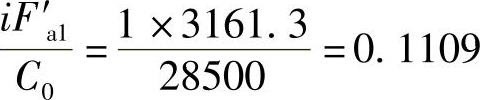
查表2-23b(或者表2-20),得.=0.4672(用线性插值法)。
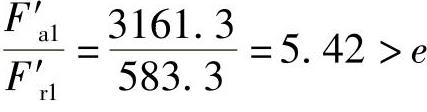
所以.=0.44,.=1.20(用线性插值法),因此
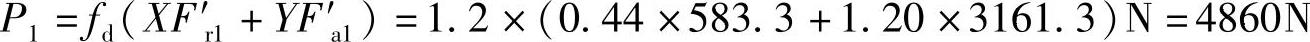
因为F′r1=F′r2,而.a1>.a2,所以.1.>.2.,则只需计算轴承Ⅰ的寿命即可。
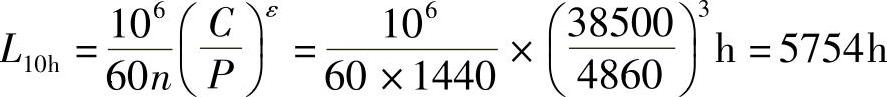
题目要求寿命大于10000h,因此不满足要求。
改选一对7309B轴承,查表2-23b,得.=1.14,则
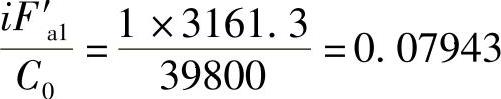
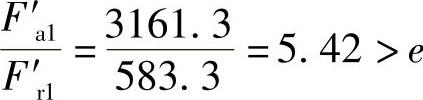
查表2-23b,得.=0.35 .=0.57,因此
. 1′=fd(XF′r1+YF′a1)=1.2×(0.35×583.3+0.57×3161.3)N=2407.3N
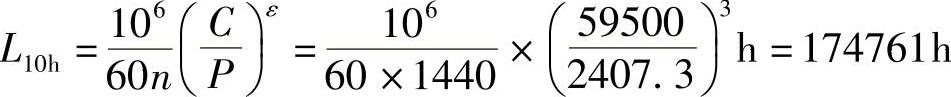
所以选用一对7309B轴承满足寿命要求,其余部分同解法一,不再赘述。
以上两种解法皆为近似解法,较精确的解法是认为此轴为三支点的轴,需精确找出固定端支点位置(并非中点处),具体方法可查有关资料,此处略。
例4 两种滚动轴承组合结构形式如图2-19所示。已知.A=600N,.R=3000N,.d=1.1,试分析轴承Ⅰ、Ⅱ所受的径向力.r、轴向力.a及当量动载荷. r,并说明哪个轴承是危险轴承。
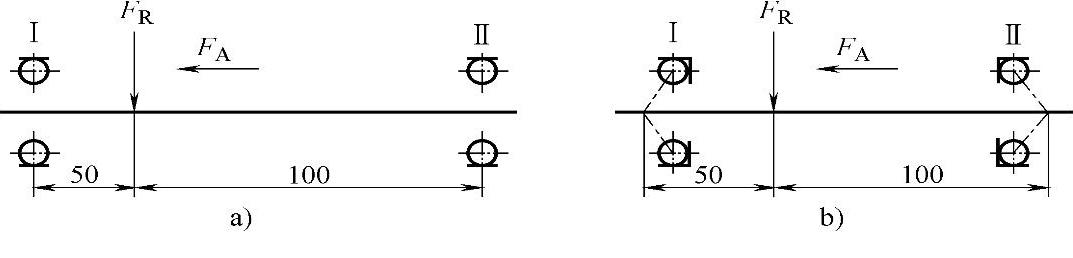
图2-19 例4图
a)6206轴承 b)7206轴承
解
(1)采用一对6206轴承(图2-19a)查表2-18,得.=19.5kN,.0=11.5kN。
轴承Ⅰ
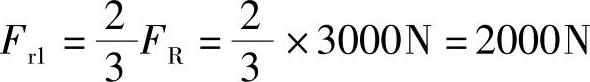
. a1=.A=600N
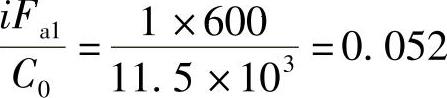
查表2-18或者表2-23b,得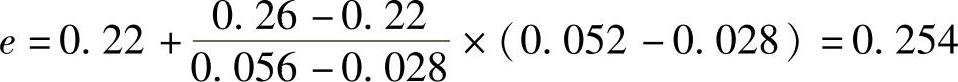
(线性插值公式)。
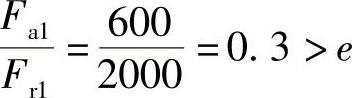
查表2-18或者表2-23b,得.=0.56,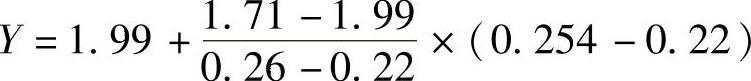
=1.752。
. 1=.d(XFr1+YFa1)=1.1×(0.56×2000+1.752×600)N=2388N
轴承Ⅱ
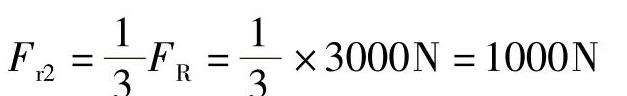
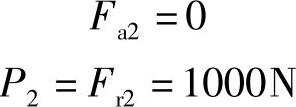
因为.1﹥.2,所以轴承Ⅰ危险。
(2)采用一对7206C轴承反装(图2-19b),查表2-20,得.=14.2mm,.=16mm,.=23000N,.0=15000N。径向力.r到轴承Ⅰ及Ⅱ支点的距离为
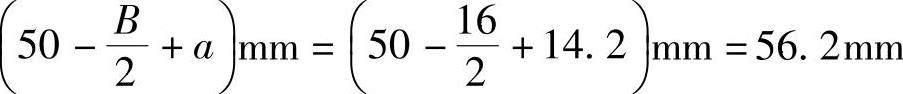
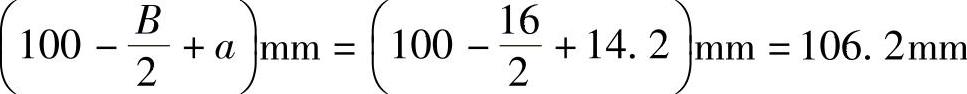
轴承的径向载荷为
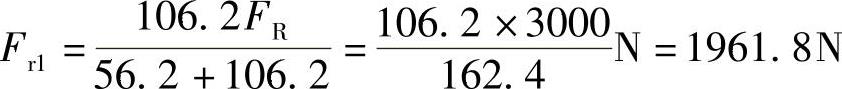
. r2=.R-.r1=(3000-1961.8)N=1038.2N
内部轴向力为
. S1=0.4.r1=0.4×1961.8N=784.7N
. S2=0.4.r2=0.4×1038.2N=451.3N
. A+.S1=(600+784.7)N=1384.7N>.S2
所以轴承Ⅱ被压紧,轴承Ⅰ被放松。
. a1=.S1=784.7N
. a2=.A+.S1=1384.7N
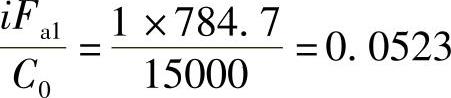
查表2-20或表2-23b得
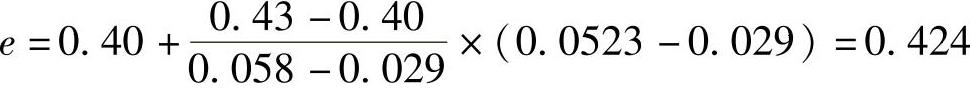
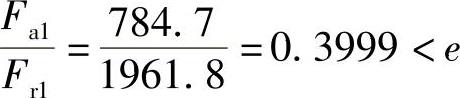
所以.1=.d.r1=1.1×1961.8N=2158N
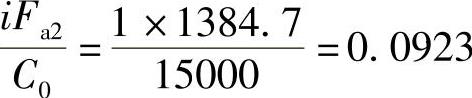
查表2-20得
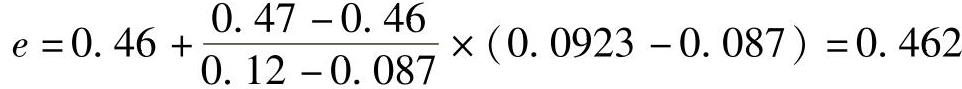
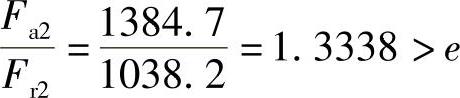
查表2-20或表2-23b,得.=0.44,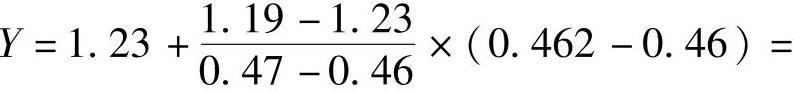
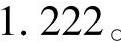
. 2=.d(XFr2+YFa2)=1.1×(0.44×1038.2+1.222×1384.7)N=2364N
. 2﹥.1,所以轴承Ⅱ危险。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




