配电网潮流计算优化方法

配电网潮流算法是配电网分析的基础，配电网的网络重构、故障处理、无功优化和状态估计等都需要用到配网潮流的数据。由于配电网结构特点都是开环运行的，配电网呈辐射状，配电线路的电阻电抗比（R／X）大，利用常规方法进行潮流计算会导致算法不收敛，而前推回代法是线性收敛的，从而解决了潮流计算收敛难的问题。

1.主干馈线配电网潮流计算

在典型的配电网络中，一般仅有根节点的节点电压固定不变，而其他节点都可视为PQ节点。如图6-3所示，配电网仅有一条主干馈线，n个节点，n－1条支路。在根节点电压和节点负荷功率已知的情况下通过以下步骤可以求出全网节点电压和功率分布。

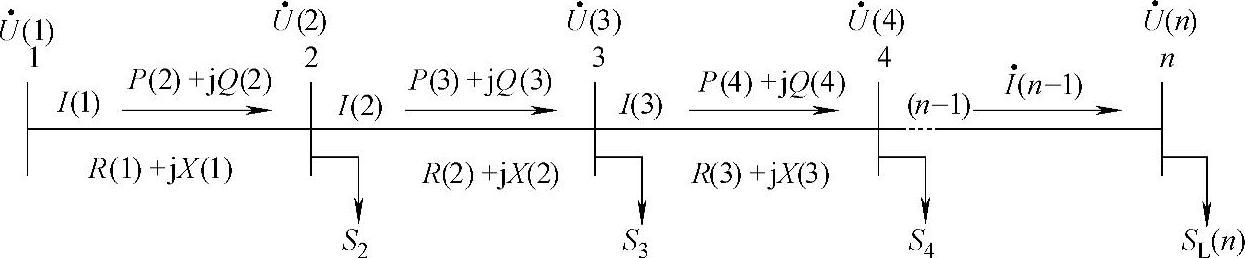
图6-3 配电网主馈线图

（1）节点电压计算

考虑1和2两节点，其电压降为

U·（1）－U·（2）=I·（1）［R（1）＋jX（1）］ （6-1）

P（2）－jQ（2）=I·（1）U·（2） （6-2）

由式（6-1）和式（6-2）可以得到两点间电压降的纵分量和横分量分别为

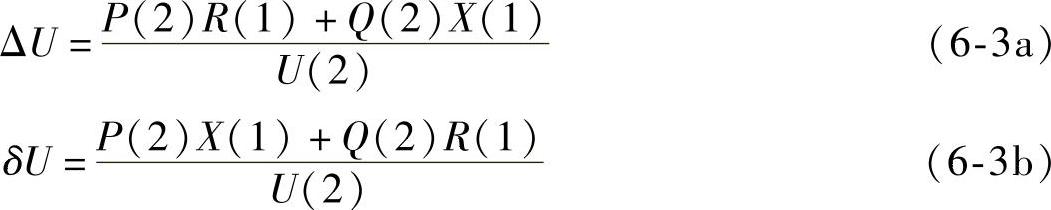
暂时忽略横分量的影响，则节点2电压幅值计算如下

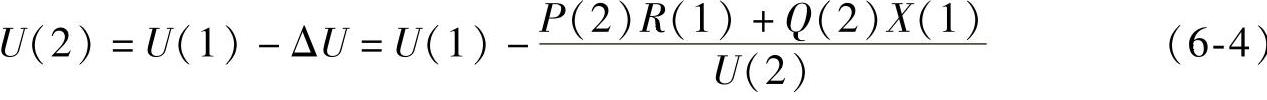
由上式可得

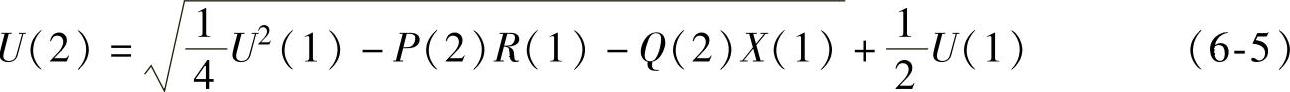
将U（2）计算结果代入式（6-3b），可计算出电压降横分量，并由下式计算两节点间相角差为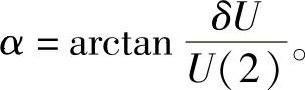

同时可用横分量对式（6-5）中计算的电压幅值进行修正。对于图6-3所示的系统，从式（6-5）式中可以得出各节点电压计算的递推公式为

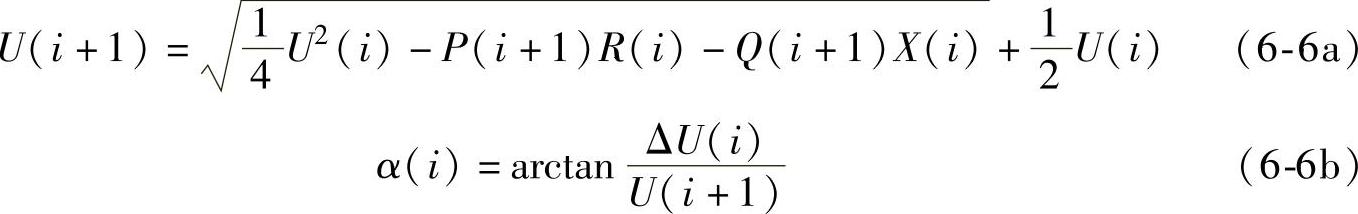
在上式中电压的单位为kV，阻抗的单位为Ω，功率的单位为MV·A。

（2）节点功率计算

1）支路功率损耗。

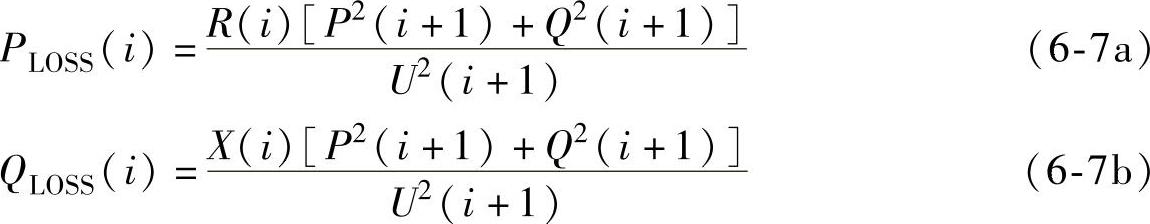
式中，i=1，2，…，B，B为支路数。

2）节点功率。

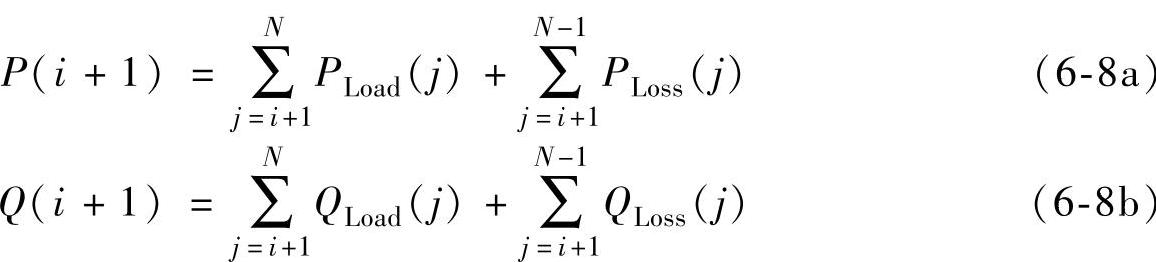
式中，i=0，1，2，…，N－1，N为节点数。

从式（6-8a）和式（6-8b）可以看出节点处的功率为节点后所有节点负荷功率和支路损耗功率之和。

（3）收敛条件

以前后两次迭代的电压偏差作为迭代收敛条件，下式表明节点电压幅值最大偏差小于设定阈值，即认为迭代收敛，则迭代过程结束。

max｛|U^K（i）－U^K－1（i）|｝＜ε （6-9）

通过以上分析得到单一分支配电网潮流计算步骤为

1）初始化，令所有支路功率损耗为零；(www.xing528.com)

2）根据式（6-8a）和式（6-8b）两式计算各节点功率；

3）根据式（6-6a）和式（6-6b）两式计算各节点电压幅值和相角增量。根据前后两次迭代的电压偏差是否小于设定阈值判断是否收敛，如果不小于设定阈值，则进行下一步，否则停止迭代过程。

4）根据式（6-7a）和式（6-7b）计算各支路的功率损耗，返回步骤1）。

2.前推回代法

前推回代法是配电网支路类算法中被广泛研究的一种方法。该方法从根节点起按广度优先搜索并对配电网进行分层编号，编号反映了前推回代的顺序。考虑到配电网的辐射型结构，其一般是由一条主馈线带有数条分支，各分支又带有各自的子分支，依此类推。定义主馈线为第一层，从左向右依次定义主馈线上的各节点，然后定义离电源最近的节点的分支线及其上的节点，每一层最后一个节点号要比它的下一层的第一个节点号小1。此方法简便、有效，利于编程，对于任何复杂的辐射状配电网的网络编号都适用。具体编号方法可如图6-4所示，其中［］代表层，（）代表支路号、数字代表节点号。

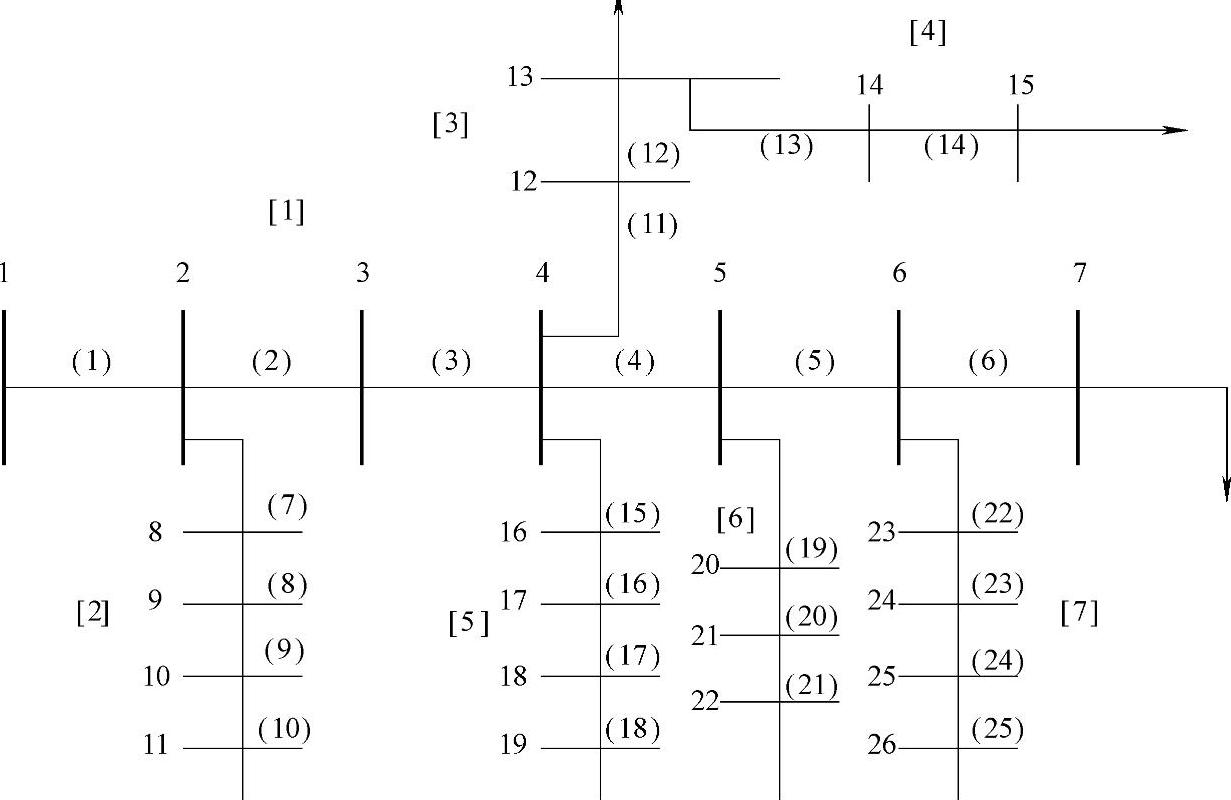
图6-4 某辐射型配电网

潮流算法如下：

（1）计算节点注入电流

I^k_i=（S_i／U_i^k－1）－Y_iU_i^k－1 （6-10）式中，U_i^k－1为k－1次迭代的节点i的电压；S_i为节点i的注入功率之和；Y_i为节点i的并联导纳。

（2）回代过程

设第L条支路的起点为节点L₁，且终点为L₂，则有

J_L^（k）=－I_L2^（k）＋∑_i （6-11）

式中，J_L为第L条支路上的电流，I_L2为节点L₂上的注入电流，∑_i为从L₂点出发的各分支支路上的电流和。

（3）前推过程

U_L2^（k）=U_L1^（k）－Z_LJ_L^（K） （6-12）

（4）判断收敛条件

前推回代法还有另外一种形式，如图6-5所示。由图6-5所示简单馈线段为例经过简单推导可以得出：

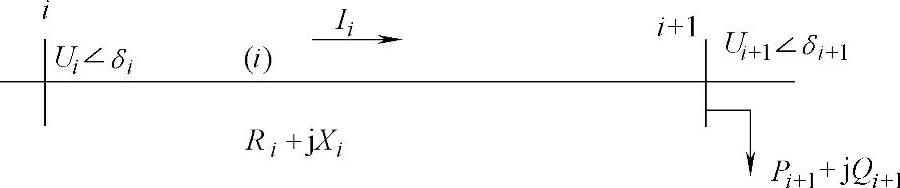
图6-5 某配电网中的一段馈电线段

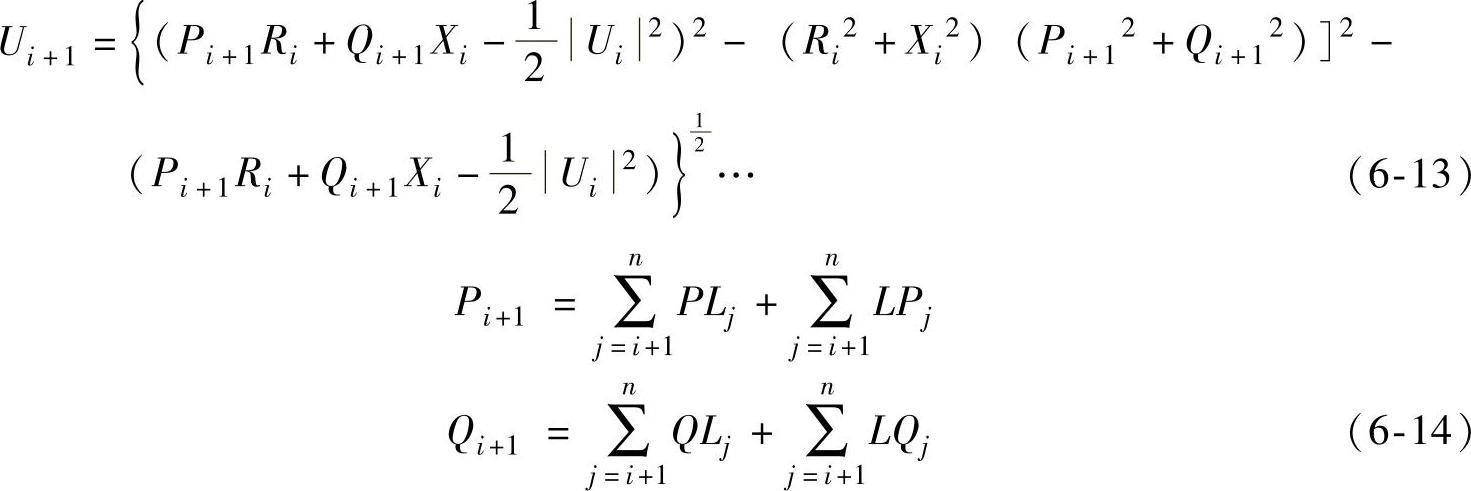
式中，PL_j和QL_j为节点j的负荷功率；LP_j和LQ_j为支路j上的线损。

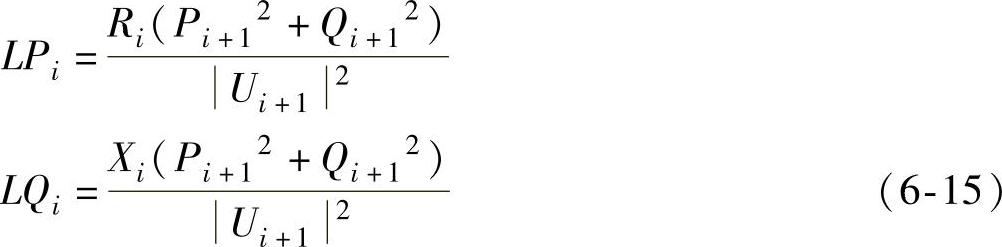
式（6-13）、式（6-14）和式（6-15）构成了前推回代的基本方法。

配电潮流前推回代算法的迭代步骤如下：

1）初始化。给定配电馈线根节点电压，并为其他节点电压赋初值。

2）考虑负荷电压静特性，计算负荷数据。

3）从各负荷节点出发，先子节点后父节点，通过前推计算，由节点电压分布求支路功率分布。

4）根节点出发，先父节点后子节点，通过回推计算，由支路功率分布求节点电压分布。

5）判断相邻两次迭代电压差的模分量的最大值max|ΔU_i|是否小于给定的收敛指标，若是，则停止计算；否则，转到步骤2）。