基于经济压差法的无功优化混合计算研究

1.经济压差的定义

在有功功率传输值与线路平均电压不变的情况下，维持输电线路无功分点刚好位于线路中点，此时线路首末两端电压之差称为经济压差ΔU_J。在上述条件下输电线路上流过的无功潮流称为经济压差无功潮流。

无功分点即是无功电流为零的点。经过研究表明，当线路上的过剩无功为ΔQ_过剩时，在线路两端等量补偿线路的无功消耗，即线路两端分别补偿－ΔQ_过剩／2，线路上的有功损耗最小，线路运行最经济。

为了便于理解，简单示意图如图4-12所示。通常线路的等效电阻、电抗、电纳均匀分布。由图可知，根据基尔霍夫电流定理，在此种补偿方式下，线路的中点无功电流为0，即是维持输电线路无功分点刚好位于线路中点，在其他补偿方式均不能达到。

图4-12 经济压差线路最优补偿示意图

2.经济压差补偿原理的数学证明

（1）空负荷运行情况下无功功率分点的最优位置

首先推导输电线路在不带任何负荷运行时，线路本身的充电电容产生的充电电流与整条线路额外产生的有功功率损耗之间的关系。

对于一条长度为S的输电线路，令其单位长度的正序电阻、等效电抗、等效电容分别为r，x，b；并假定此条输电线路的无功功率分点（即是容性无功电流为零处）位于线路首末之间某处，而此分点与线路首端距离设为l₀，则与线路末端的距离则为－（S－l₀）；线路示意图如图4-13所示。

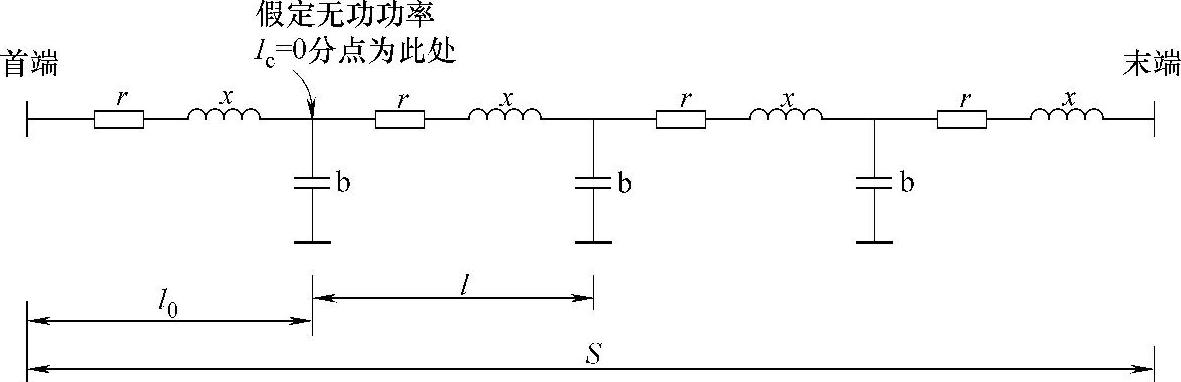
图4-13 线路等效参数

在无功电流I_c=0相距为l的地方，假设此处的相电压值为U_p，则其充电容性电流为

I_c=blU_p （4-84）

那么，对于l处相邻的微小段dl上的电阻则为Δr=r×dl，那么在此段dl长度上的电阻有功功率损耗为

显然dl上的三相有功功率损耗值为3dP_ploss，由于U_l=3U_p（U_l为线电压），则有3dP_Ploss=3b²l²U²_prdl=b²l²U²_lrdl。令l₀／S=x，其中，x则为［0，1］之间任意值。为不失一般性，取输电线路首末两端的电压平均值U为计算电压进行计算，可以推出由于等效电容的存在，在整个输电线路上造成的额外有功功率损耗为

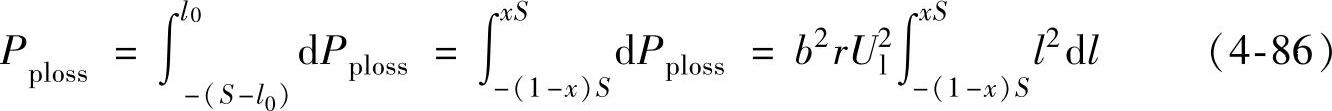
进一步进行化简则有

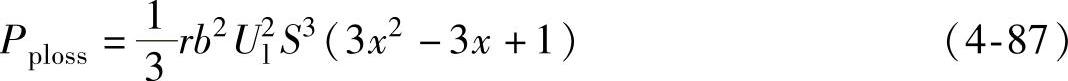
由于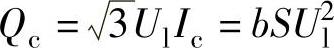，即为整条输电线路的总充电功率，那么也可以将上式表示为

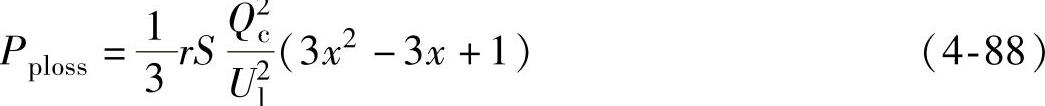
在上式中仅有x是未知变量，为了探讨其在可行域［0，1］中的最优值，对x求导则有

对x求二阶导数，可得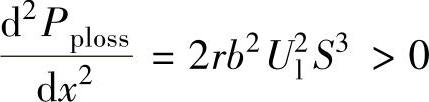。所以P_ploss存在最小值，当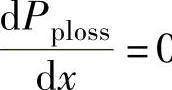0时，取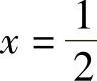即为最小值。

由此，表明当无功功率分点位于输电线路的中点时，输电线路上的有功损耗最小，其最小值为

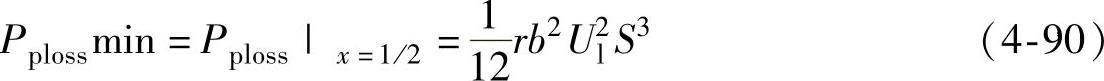
而当无功功率分点位于输电线路的首端或是末端的情况下，输电线路上的有功损耗值为

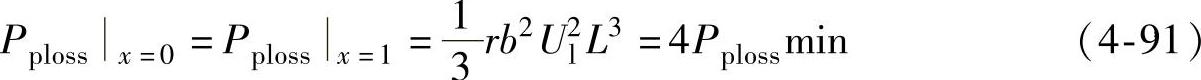
可以发现，在输电线路空负荷情况下，如果使得无功功率分点处在输电线路的中点，那么可以使得线路有功损耗值在理论上达到最小。图4-14为有功功率损耗大小与无功功率分点位置的关系图，其中取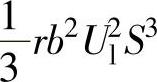为有功损耗的单位值。

通过上述证明，可以得出如下结论：

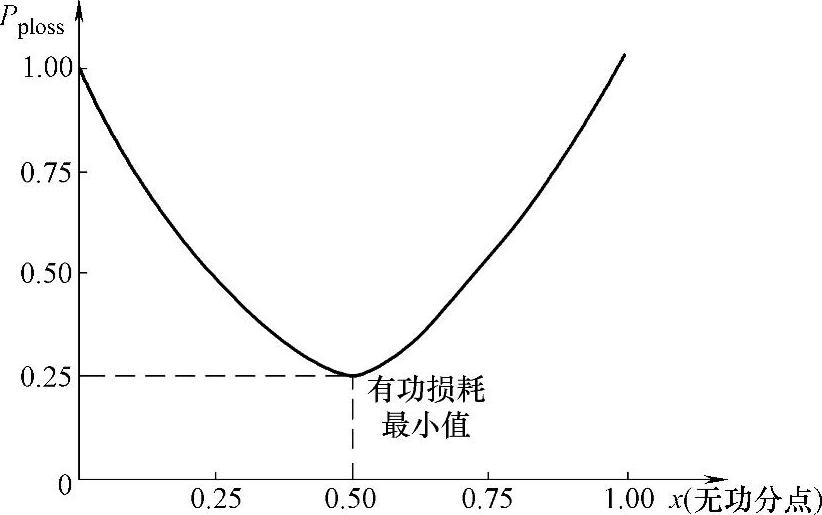
图4-14 P_ploss值与无功功率分点x位置的关系

1）在输电线路中，其等效的充电功率造成有功功率损失与线路的等效电阻成正比，与线路等效电容的二次方成正比，同时也和输电线路线电压的二次方成正比，并且与整条线路的长度的三次方成正比。由于等效电阻、电容均与输电线路的长度相关，所以越长的、电压等级越高的输电线路等效的充电无功功率的影响越不能忽视。

2）无功功率分点的位置决定了输电线路等效充电功率所产生的有功功率损耗大小。上述推导表明：在线路两端进行等量的无功功率补偿可以使得无功功率分点位于输电线路的中点，此时的有功功率损耗值最小，这就是经济压差潮流算法的根据。

（2）带负荷运行情况下无功功率分点的最优位置

自然功率P_λ又称为波阻抗负荷，是表示输电线路的输电特性的一个特征参量。当线路输送有功功率为自然功率时，输电线路等效电抗上的无功消耗与等效电容的无功产生正好平衡，在线路的首端和末端既不产生也不消耗无功功率。在线路输送自然功率情况下，单位长度上对地电容产生的无功与线路电抗吸收的无功相等，而且线路两端的功率因数保持一致，电压和电流沿着线路线性平坦分布。

当输电线路上输送功率小于自然功率时，此时充电功率将大于线路消耗无功，会导致线路末端电压高于首端；相反，当线路输送功率大于自然功率时，由于无功不足，需要额外的无功补偿，在没有无功补偿时，线路电压就会下降，如图4-15所示。

上文中提到，由输电线路上的电容产生无功功率与电抗上消耗的无功功率之差Q_C－Q_L=ΔQ，称为过剩无功功率。在输送的有功功率不等于自然功率时，过剩无功往往不为0。此时线路上的过剩无功功率有如下关系：

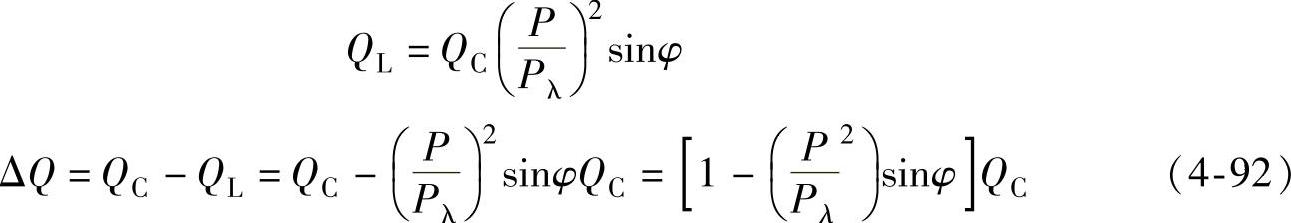
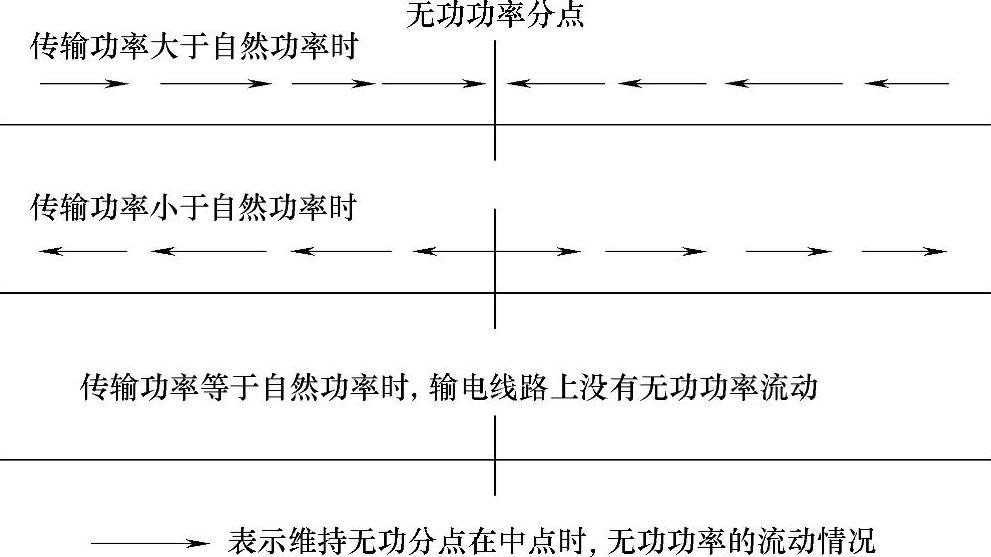
图4-15 不同传输功率下经济压差无功潮流的形式

式中，P为线路上输送的有功功率；P_λ为自然功率；φ为线路的阻抗角；Q_C为线路充电功率（Q_C=bU²）。

对于110kV及其以上电压等级的输电线路，通常情况下r＜＜x即sinφ≈1

那么上式可简化为

与空负荷线路相比，带负荷运行时线路上微小段dl上由于输送无功功率而造成的有功功率损耗的计算式将多一个因子，即

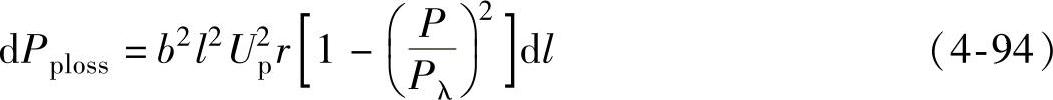
其余的推导步骤与空负荷情况下相似。按照空负荷时相同的线路模型，最终得到在带负荷运行时，线路上输送的无功功率在整条线路上造成的有功损耗为

3.经济压差最优潮流下理想无功布局

（1）无功功率就地补偿

就地补偿和分层平衡是无功功率补偿的基本原则，同时也是实现全网经济压差潮流基本条件。在所有的电网中，按照各自的作用不同，均可将电网中的各元件大致地分为发电厂、输电线路、降压变电站以及用电负荷。

发电厂一般由发电机、电厂自用设备和升压变压器组成。在发电过程中，发电机上流动的励磁无功与厂自用设备以及升压变压器上消耗的无功功率均可以通过调节发电机的励磁电力来满足。而且，发电机的励磁调节可以做到动态平滑的连续调节，可以根据发电厂的运行情况随之改变，从而维持升压变压器高压侧尽可能少地向系统输入无功功率，能够做到发电厂的无功功率就地平衡。

降压变电站中有主变压器、站用变压器，而且有些主变压器低压侧会带负荷。保持变电站的无功功率就地平衡需要在补偿母线上装设足够容量的低压无功补偿装置，尽可能地保证变电站主变压器高压侧尽可能少的与系统进行无功功率交换。对于电力负荷，理论上也能够进行完全就地补偿。电网就地平衡时无功补偿情况如图4-16所示。

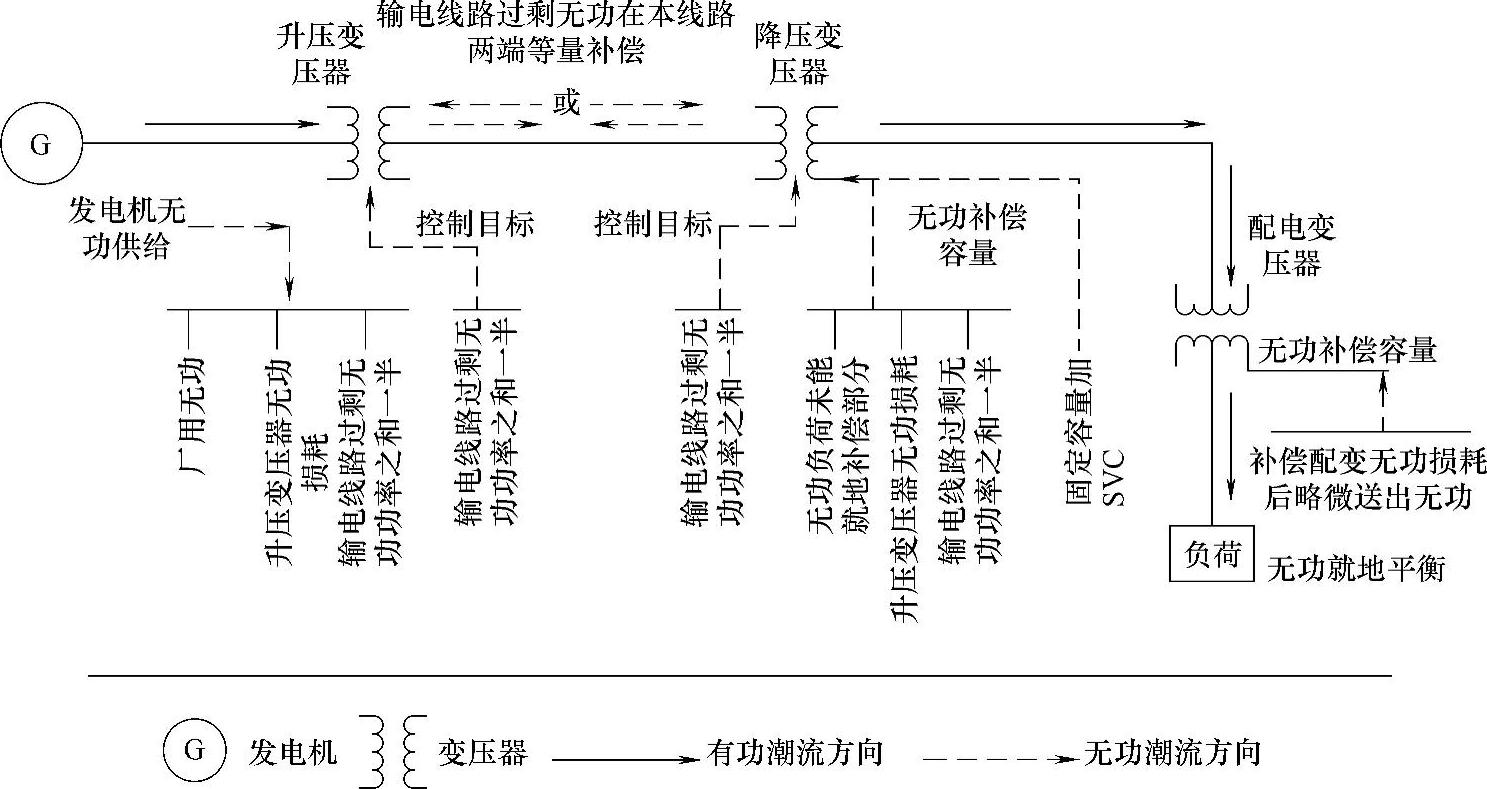
图4-16 地区电网就地平衡无功补偿

在上述三个元件均已实现就地平衡的理想状态时，输电线路却不能实现沿线动态无功功率平衡。而输电线路上流动的无功功率大小将直接影响线路上的有功损耗与电压降落。在上文中已证明，在输电线路两端对线路损耗进行等量补偿时即为最经济的运行状态。在其他元件就地补偿的情况下，输电线路上只流动过剩功率的一半ΔQ_过剩／2。如图4-17所示，整个电网几乎不流动无功功率，是经济压差最优无功潮流的理想状态。从物理意义而言，即是通过合理的无功补偿，改变线路的对地电容值，实现线路上产生的容性无功刚好等于消耗掉的感性无功，整条线路上不产生额外的无功损耗。

（2）无功功率分层平衡

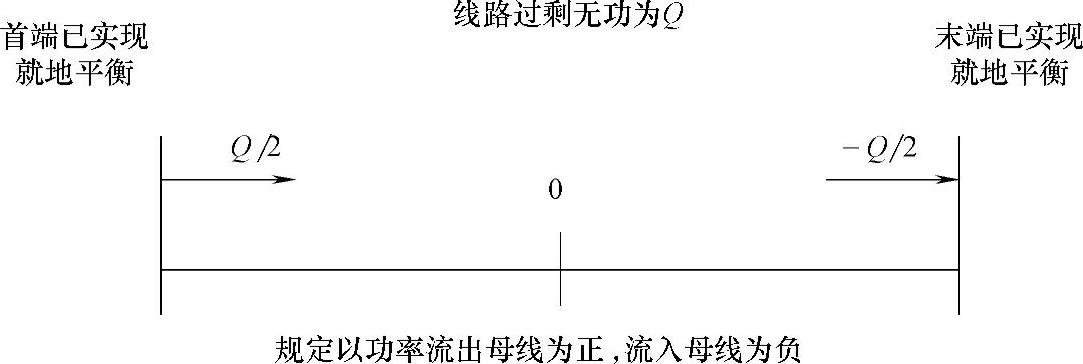
图4-17 经济压差最优无功潮流的理想状态

大多数无功优化方法将各个电压等级一起进行优化，而在经济压差无功优化算法中，是将以变压器为单位实现分层优化。如果地区电网的结构与有功功率情况不变，以各个变电站为一个节点单位，那么各个书点高压侧注入电网的无功功率大小是实现电网经济压差最优无功潮流的主要因素。所以本书在进行地区电网无功电压优化时，先将多个电压等级的电网进行电压分层。这样既可以减少控制变量，又能提高收敛性，使得同一电压等级的层面处于最优运行。对于地区电网而言，通常按照电压等级可分为220／110／35kV三层。

对同一个电压层面而言，变压器的高、中压侧母线所连线路过剩无功之和的一半需要在变压器补偿母线进行分层平衡，而不穿越变压器流入另外一侧电网，要使无功功率尽可能少地流经变压器。在图4-18中，以变压器为单位，实现了无功功率分层平衡。

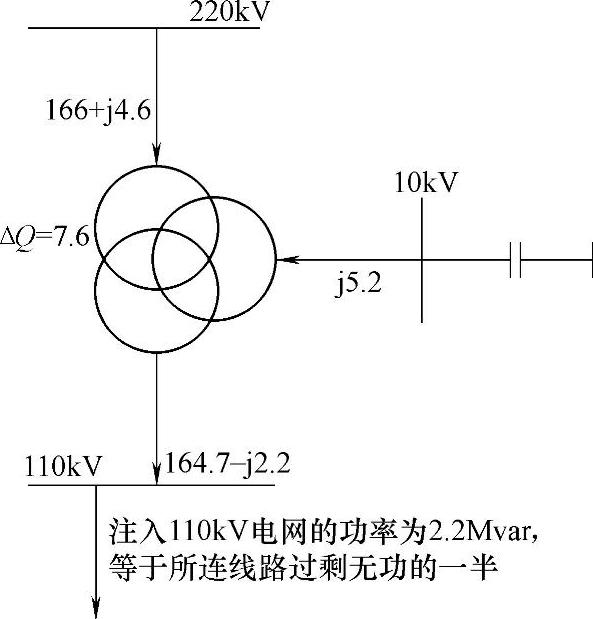
图4-18 无功分层平衡示意

图4-18中，流向110kV电网的潮流即是最优无功潮流。为了达到此效果，首先需要在10kV用户端做到就地平衡，并满足整个变压器的无功功率平衡式：

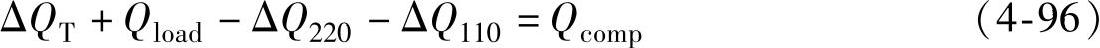(www.xing528.com)

式中，ΔQ₂₂₀为220kV母线上连接线路过剩无功功率的一半；ΔQ₁₁₀为110kV母线上连接线路过剩无功功率的一半；ΔQ_T为整个变压器的无功损失；Q_load假定已经实现了无功功率补偿，此时令其为0；Q_comp是在低压侧母线上的补偿容量，对应图上的数值为7.6＋0＋2.2－4.6Mvar=5.2Mvar。这种情况下，变压器的110kV母线向系统输送的无功功率值恰好即为线路实现自身就地补偿的值，在负荷就地补偿的条件下达到最优潮流。

（3）变电站理想的补偿容量

根据经济压差无功功率就地分层平衡的基本原则，得到在经济压差最优潮流下各变电站的最优无功补偿如下：

1）经济压差最优无功潮流下220kV变电站无功补偿容量。

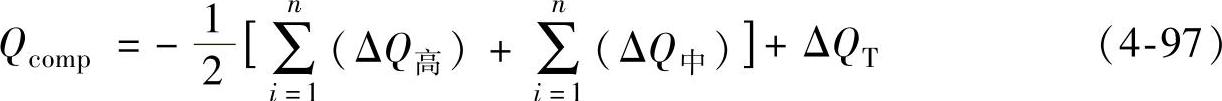
式中，Q_comp为整个变压器所需补偿容量；n为变压器母线所接输电线路条数；ΔQ_高 为变压器高压侧母线相连线路过剩无功之和；ΔQ_中 为变压器中压侧母线相连线路过剩无功之和；ΔQ_T为变压器无功损失。

2）经济压差最优无功潮流下110kV变电站无功补偿容量。

式中，Q_load为低压侧无功负荷负荷。与220kV变电站略有差异，在110kV变电站进行无功补偿容量设计时，需要将低压侧无功负荷就地进行补偿，减少无功功率流入下级电网。其他计算参数与220kV变电站类似。

4.传统经济压差算法

在传统经济压差求解中，将电网中的变压器作为一个计算单元，求得变压器高压侧节点注入电网的最佳无功功率值。以往的无功优化通常单纯地以网损最小为目标函数，而经济压差算法在满足电网中各高压侧节点之间的输电线路上的电压降落纵分量为最小的同时，达到线损最小。其目标函数为

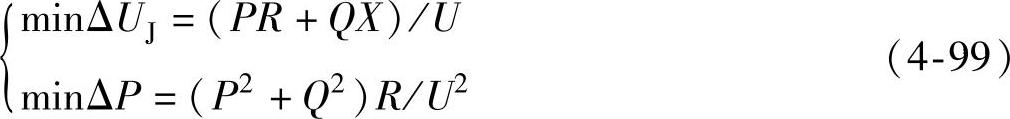
在进行经济压差潮流计算时，将潮流计算中的部分约束（如无功出力上下限，档位调整上下限）暂不考虑，而只考虑节点电压约束，并将发电机无功设定为连续调节。经济压差算法中不考虑变压器内部情况，所以档位变量K不直接参与计算，设为靠中档运行，之后根据低压侧电压情况决策出档位动作值。

通过潮流计算之后得到各条输电线路上的过剩无功情况，从而求出变压器高压侧母线注入电网的无功功率优化值Q_opt、高压侧母线的优化电压U_opt以及之前求出的变压器整体无功补偿值Q_comp。通过微调Q_comp的大小，使变压器高压侧注入电网的实际无功功率Q_实等于优化值Q_opt。

5.基于经济压差法的无功优化混合计算方法

传统的经济压差算法考虑了电网无功补偿的就地平衡基本原理。但是，对于实现经济压差潮流的算法未能给出清晰的优化过程，对于优化控制的具体实现尚未给出明确的策略，而且无法确定分层节点的电压最优值。传统的经济压差算法仅适用于电网中存在大量动态无功补偿装置的情况，这在当前的技术水平往往很难达到，是一种前瞻性较强而实用性偏弱的无功优化算法。

针对这种情况在传统经济压差最优潮流的研究基础上，本节通过对优化算法进行详细的推导，提出新的基于经济压差法的无功优化混合迭代求解方法，并构造动态无功源进行实用化处理，而且对于分层节点优化电压的计算选取也给出了解决方案，对迭代判据也进行了改进。通过改进，提高了经济压差优化算法的收敛性和实用性，使之能够实际应用于地区电网的无功电压优化。

（1）经济压差最优无功初值计算方法

当电网处于经济压差最优无功潮流的理想状态下，此时各个变电站完全能够满足就地平衡的原则。由此可以得到该状态下变电站的理想补偿容量，并可以将其作为无功迭代计算的初值。由此，构建其经济压差最优补偿容量初始值计算子模块的计算流程如图4-19所示。

（2）基于经济压差法和灵敏度分析的混合迭代方法

根据经济压差最优无功理论，整个电网实现经济压差最优无功潮流的理想情况为：电网中的所有元件均需要实现完全的就地补偿，并且能够跟随负荷的变化情况动态地调整无功出力。此时根据经济压差补偿原理将线路损耗在两端进行等量补偿，将使整个电网处于最优无功潮流的状态。传统的经济压差算法可以通过此最优状态计算出各节点的最优无功补偿，但对于如何达到此最优状态未进行深入的探讨。此外，传统的经济压差算法要求各节点均能够平滑动态地调节无功。对于发电机节点而言，在一定调整范围内能够实现此要求，但对变压器而言，当前主要的补偿设备仍是并联电容、电抗器。虽然电力电子技术发展迅猛，但在现阶段仍无法在所有的变压器均装设SVC、STATCOM等补偿设备，所以变压器节点不能动态平滑调节地调整无功功率，在某些极端情况下有些节点甚至没有配置任何的无功源。所以如何利用当前的控制手段，对经济压差算法进行实用化改进，尽可能地使电网处于最优运行也是本节解决的问题。

1）最优无功补偿的迭代求解。

传统的经济压差算法是在实现经济压差最优潮流的前提下，通过就地补偿的原则求取的各节点最优无功补偿值。但是对于达到这一最优的无功潮流的具体方法研究较少，而且按照传统的经济压差理论进行无功补偿之后，电网的无功潮流将会发生改变，此时用于求取最优无功补偿容量的计算参数也会发生变化。因此，采用迭代求解与灵敏度分析相结合的方式，通过迭代方式的探究，给出了基于经济压差法的最优无功值的详细迭代求解过程。

在进行迭代求解节点最优无功补偿容量时，尝试了如下两种思路：

① 以节点的注入无功功率Q为迭代变量，迭代步骤如下：

a）利用经济压差最优无功初值计算模块求取Q_comp初值，在各个节点上按照此补偿参数进行无功补偿；

b）对于计算网络而言，在补偿初值带入之后，相当于节点无功负荷的计算参数发生变化；对无功负荷参数进行修正，重新进行潮流计算、迭代求解Q′_comp；

c）当各节点的Q_c′_omp值在前后两次迭代计算之后变化很小时，得出变压器无功补偿容量的最终值。

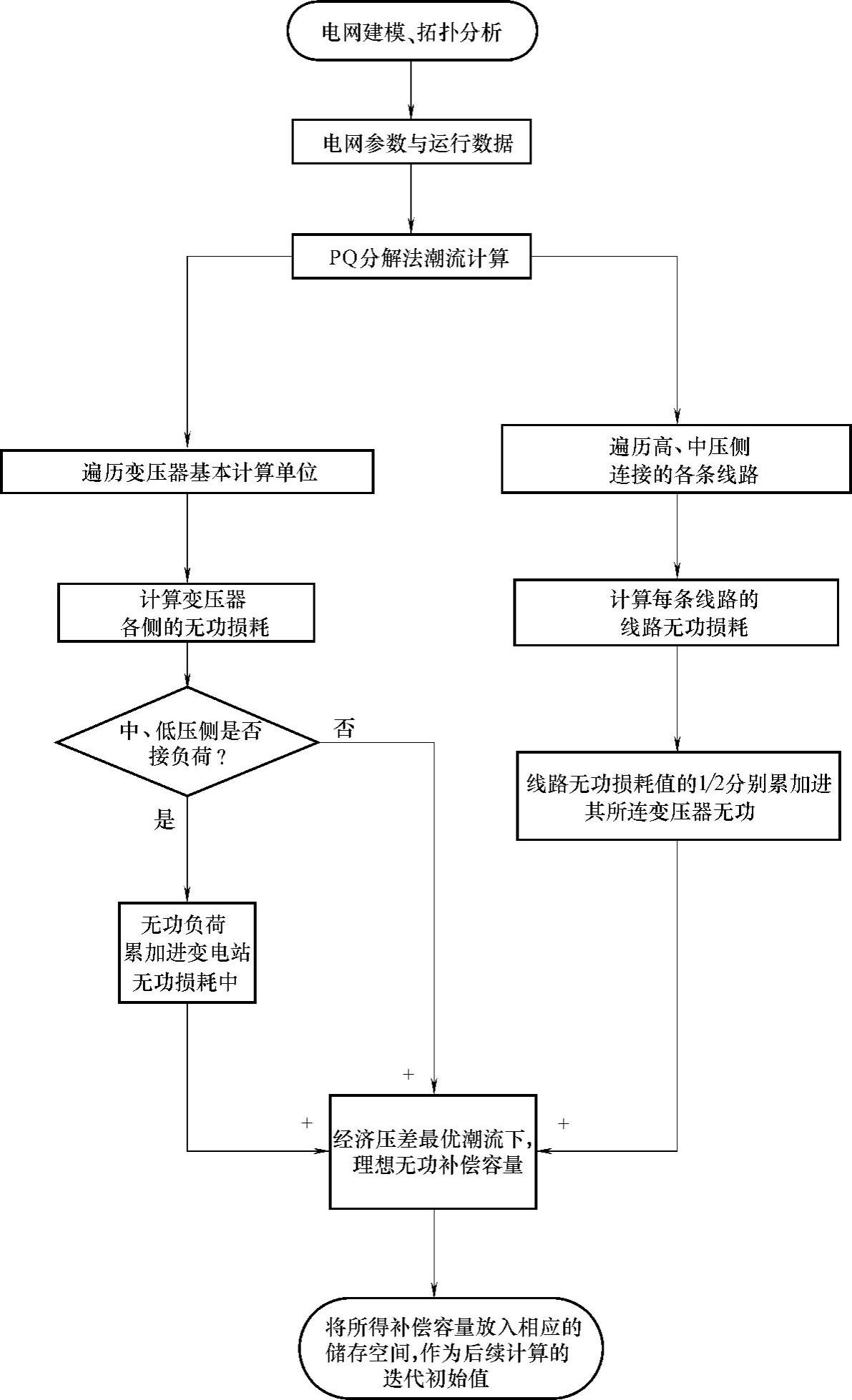
图4-19 经济压差最优无功初始值计算模块

根据这种思路计算，发现该方法在计算中不容易收敛，而且对于潮流迭代的初值要求很高。这种迭代思路相当于将所有的变压器节点均看作PQ节点，可以随意控制其注入无功大小，却未考虑电压约束，任其节点的电压变化波动。与传统的经济压差算法思想类似，试图通过仅改变节点注入无功进行无功优化。然而，随着系统中PV节点的减少，使得电网的电压支撑能力降低，导致整个系统的收敛域变小，最终导致潮流计算不收敛，算法鲁棒性较差。

② 以节点电压U为迭代变量，考虑节点无功／电压之间的紧密联系，利用PQ分解法形成的B″，计算无功电压灵敏度矩阵，迭代步骤如下：

a）利用经济压差最优无功初值计算模块求取Q_comp初值，在各个节点上按照此补偿参数进行无功补偿；

b）利用全网无功／电压灵敏度矩阵，将初值带入之后求取各节点新电压幅值；对各节点电压幅值进行修正，重新进行潮流计算，迭代求出新无功补偿容量值Q′_comp；

c）当各节点的Q′_comp值在前后两次迭代计算之后变化很小时，得出变压器无功补偿容量的最终值。

经济压差算法的计算前提是各个节点有充足的无功，所以可设定其为PV节点。在迭代过程中，充分考虑到了电压的约束条件，整个系统有足够的无功电压支撑，易于收敛。而且在求解过程中，可直接利用PQ分解法时自动生成B″矩阵求解无功电压灵敏度矩阵S，提高了程序利用率。

2）动态无功源控制空间的构造。

根据传统经济压差算法的要求，每个节点都能够精细地调整无功出力。但是在实际电网中，具有调相能力的发电机、SVC、STATCOM等装置才具有精细准确的无功调节能力，普通变压器节点往往无法达到此要求。在本小节中，通过对此进行了实用化改进，使之等效地实现经济压差优化效果。通过构造了一个动态无功源的控制区间［50］，从动态无功控制源的控制力入手；然后从该控制区间中，选取最具控制力的动态无功源进行等效补偿，解决部分节点无法精细调节无功功率的问题，使之能够在现有的控制条件下最大限度地实现经济压差优化。

设整个电网中有d个动态无功源，构成集合D，有m个无法自身动态无功调节的节点，构成集合M。构造动态无功控制源的步骤如下：

① 对于属于集合D中的第j个动态无功源，将其设置为PQ节点。对于其他的动态无功源，如果是发电机节点，可以假定其AVR调节速度足够快，能够保持机端电压不变，将其设定为PV节点；当其调节范围处于极限时，则按照PQ节点处理。如果是SVC、STATCOM这类无功源，则将其考虑为PQ节点。在计算所有节点的无功电气灵敏度时，应包含PV节点的全维增益矩阵B″；同时在PV节点所对应的对角元上加上一个很大的正数，这样就能保证在进行无功调节时不对其产生影响，反映了PV节点的对电压的控制能力。

② 在第一步的基础上，可以求解动态无功源j对于集合M内所有节点电压的控制灵敏度－［B″］^－1，对于无法自身动态无功平衡的节点i（i∈M），表示为S_ij。该数值越大表明动态无功源j对节点m的控制力越强，相应的电气距离就越小，反之则控制力越弱。

③ 对于集合M中的每个动态无功源都通过步骤①、②进行控制力求解。

④ 将各个动态无功源节点的控制能力看做一个一维的d无功控制空间。在此空间中，使用d维矢量（S_i1，S_i2，…，S_id）来描述动态无功源节点i的控制力。

利用在B″矩阵相应的对角元上加一个非常大的正数，可以模拟具有快速调节能力的动态无功源能够维持其自身电压不变的物理响应，而且此物理响应也将对与它关系密切的负荷节点产生影响。在求逆B″矩阵求解灵敏度时，该节点路集上的节点都会受到对角元极大数的影响，相邻的矩阵元素将相应的成为一个较小的数，反映在物理意义上即与该动态无功源相邻的节点电压变化也较小。

在此d维矢量空间，第j个分量充分体现了第j个动态无功源的控制能力。在改进经济压差算法优化计算时，对于自身无法实现精细无功平衡的节点i，其所需的无功功率值将由选定控制力最强的动态无功源j进行分担，且存在如下关系：

a）ΔU_i=S_ij ΔQj，即动态无功源j无功功率变化时对节点i的电压影响；

b）ΔU_i=S_ii ΔQ_i，即节点i自身无功功率变化时对自身电压的影响。

如果上述两种手段使得节点i电压的变化有相同的效果，则有S_ij ΔQ_j=S_ijΔQ_i，即是ΔQ_i=S_ij ΔQj／S_ii。如果令α=S_ij／S_ii，则有ΔQ_i=αΔQj。上式表明，对于自身无法无功平衡的节点i，可以通过动态无功源j进行无功分担，其等效无功补偿值可以用上式近似表示，这样就能够较好地解决传统经济压差算法的实用性问题。

3）迭代判据的改进。

传统的经济压差算法以单个变压器为单位，当其高压侧母线注入电网的无功功率达到优化值Q_opt时，判定其计算终止，并采用基于九区图的无功电压控制策略。显然，传统的方法仅实现了局部变压器的优化，而且基于九区图的控制方式容易造成控制振荡，难以实际操作。在本节中，首先假设待优化的电网中各个节点均有充足的平滑调节的无功源，并将这些离散量当做连续变量处理。将收敛判据改进为：max Q_i＋1－Q_i＜ε（其中，Q_i为第i次迭代计算之后无功补偿优化解）。该语句的含义为：在经济压差最优无功潮流下，各节点的最优无功出力是确定的，那么可取所有节点的前后两次优化迭代值之差的最大值进行判定。如果此最大差值都小于某一个正数ε，可以认为此时全网已经达到经济压差最优无功潮流的无功分布，该值即为最优无功补偿值。按照此判据，可以避免局部最优，并且具有可操作性。在实际操作中，对于并联电容器这样的离散无功源，电容器补偿最小单位通常为0.3Mvar，不妨取ε=0.3Mvar作为判定值。

4）分层平衡节点电压幅值的实现步骤。

在传统的经济压差算法中，仅考虑了同一电压层次上的无功优化，对于分层界面上的电压水平未能给出优化方案。在经济压差最优潮流的下，各节点之间电压降比较小，整个电网电压水平紧凑。同一电压层面上平衡节点的电压幅值大小，对于电压质量和网损均十分重要。平衡节点的电压幅值应该通过一定的办法选取，而不应该固定在原来的值。根据电网安全优质运行的原则，可以按照如下标准选取：达到全网网损最小，且满足各节点电压都合格的电压值作为同一电压层面上平衡节点的电压幅值。

不失一般性，令平衡节点的电压合格范围为0.95～1.15，不妨以0.1为一个调整单位，遍历计算。若存在不合格节点电压，则在网损值上加上大数，最后选取网损值最小的平衡节点的电压幅值。在地区电网无功电压控制中，出于安全因素，变压器分接头在同一时刻仅能调节一档，此约束条件刚好能够缩小电压优化值的解空间。

5）混合迭代算法实现步骤。

通过上述实用化改进和利用基于经济压差法的混合迭代方法，求取最优无功补偿容量Q_comp的具体步骤如下：

① 搭建电网模型，并进行网络拓扑分析，输入电网参数与运行数据。

② 调用PQ分解法潮流计算子程序，计算全网初始潮流，并将无功电压灵敏度矩阵B″存入相应的存储空间。

③ 调用经济压差迭代初值计算模块，计算出无功补偿容量初值Q₀

④ 根据初值Q₀，通过无功电压灵敏度矩阵S计算出各母线电压新值，并将其修正。重新调用潮流子模块与初值计算子模块，得到最优无功新值Q₁。

⑤ 判断max|Q_i＋1－Q_i|＜ε是否成立。如果不成立，则循环进入③；否则，则输出Q_i＋1作为最优无功补偿值，并将此时的全网网损放入储存空间。

⑥ 选定平衡节点电压幅值，如果此时各节点电压合格且网损最小，则选定此值为平衡节点电压幅值；否则，改变其电压幅值大小，重新进入③进行迭代计算。

⑦ 判断节点i的无功源性质；分两种情况：如果是动态无功源，则直接以Q_i＋1作为最优无功值；如果离散无功源的节点，按照与Q_c′_omp最接近的离散无功值进行无功补偿，之后在其动态无功源控制空间中寻找最具控制力的动态无功源进行差额等值补偿。由于差额往往较小，只需微调动态无功源的无功出力；如果该点不具有无功补偿能力，则其无功补偿值完全由动态无功源等效补偿。

综合上述步骤，适用于无功优化的改进经济压差算法流程如图4-20所示。

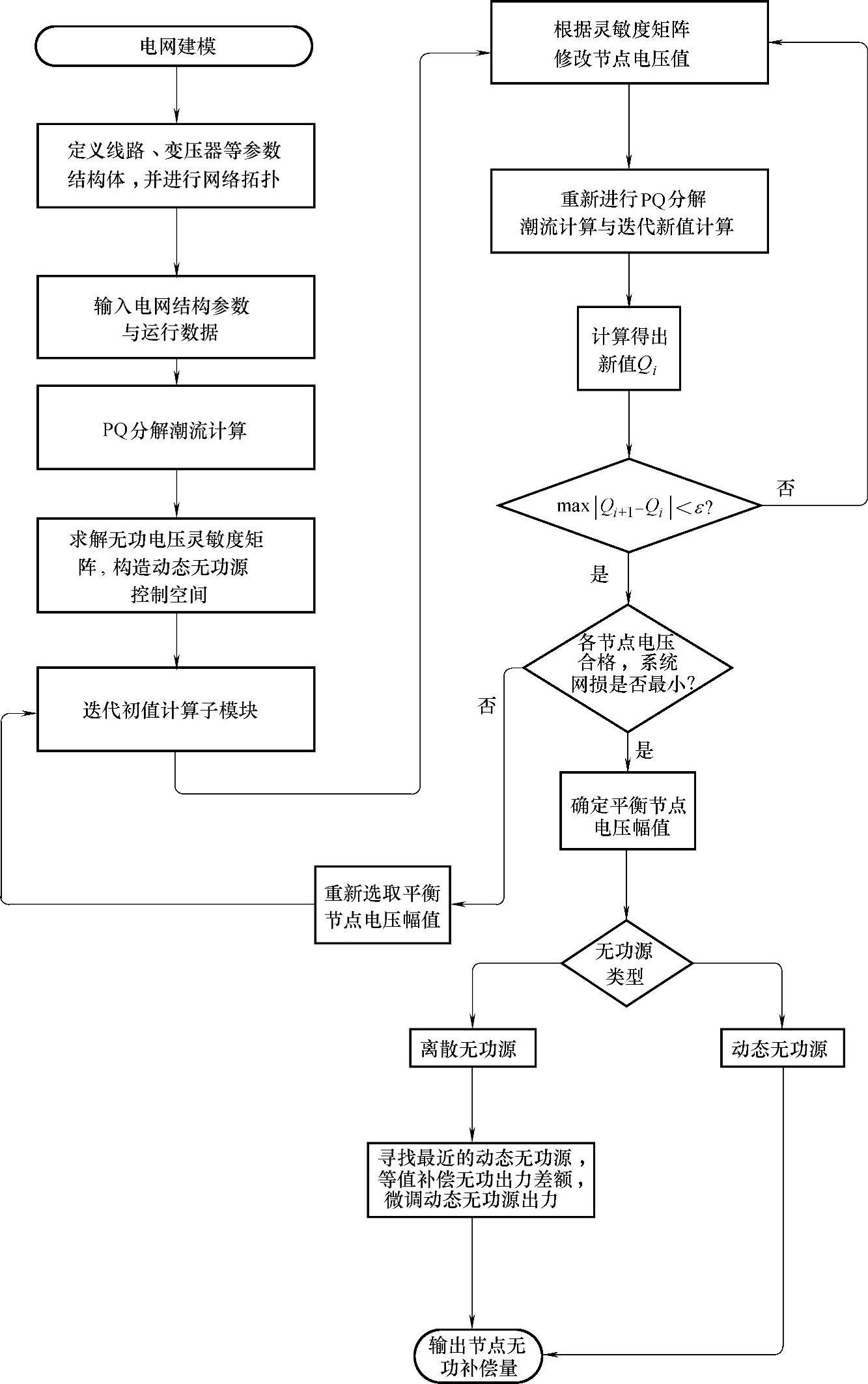
图4-20 适用于无功优化的改进经济压差算法流程