改进Deb的NSGA-Ⅱ算法研究

基于NSGA-Ⅱ算法在前期未能充分利用精英解参与交叉和变异操作，致使获取精英解的收敛速度降低，并且存在人为主观因子，以及NDS排序未能充分考虑周围的点的信息，降低了前期和中期结果的多样性。基于此，结合单目标优化算法，排序时考虑前一级Pareto排序值节点的在该个体周围的拥挤（密度）信息，提出了NSGA-Ⅱ的改进算法INSGA算法。

1.累积排序适应度赋值策略

NSGA-II的NDS排序赋值方法有一个很大的缺点：个体的Pareto排序值有时不能很好地反映个体周围的密度信息，如图4-5所示。尽管个体1周围种群的密度大于个体2周围的种群密度，但它们的Pareto排序值都为2。尽管NSGA-Ⅱ算法中有密度信息估计的部分，但所采用的密度信息的估计仅限于同一级非支配个体集中，对于图4-5中的个体1和2仍然具有同样的机会繁殖后代，这是不希望看到的。因为我们希望个体2周围的繁殖后代的能力强于个体1周围的繁殖后代的能力。针对这个缺陷，提出了累积排序适应度赋值策略。

累积排序适应度赋值策略同时还考虑了个体的Pareto排序值和密度信息。首先，类似于NS-GA-Ⅱ对所有的个体进行Pareto排序，得到每一个个体的Pareto排序值。设在第t代种群中支配个体y的个体集为y₁，y₂，L，y_n，则个体y的累积排序值定义为支配个体y的所有个体的Pareto排序值的和，即

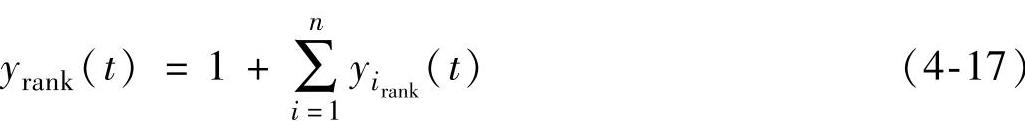
因此，个体1的rank值为5，个体2的rank值为3，而不是NDS排序中因它们都处于第二级Pareto Front Line上而赋值均为2。

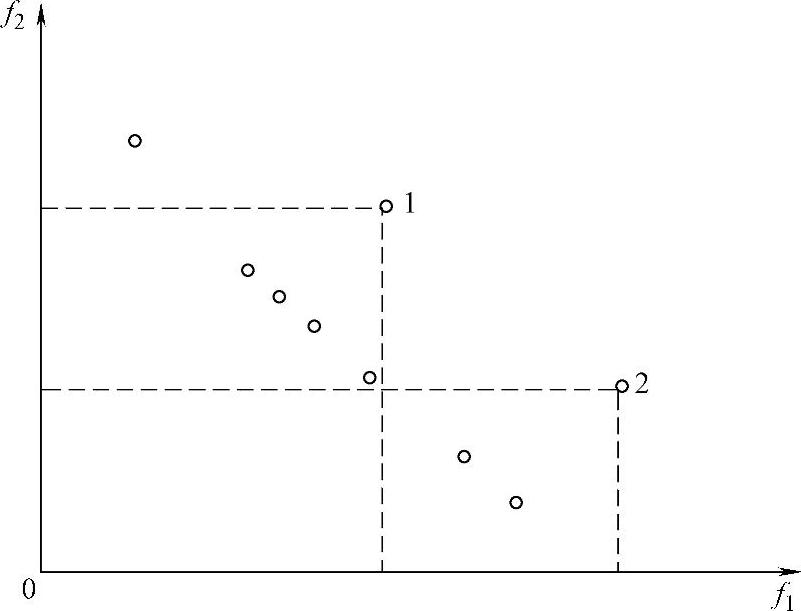
图4-5 个体周围种群密度影响的示意图

在种群P上应用累积排序适应度赋值策略的过程如下：

首先，找到群体中所有n_i=0的个体，将其存入第一级非支配个体集F₁，这些个体的Pareto排序值和累积排序值都为1。然后，对于F_i（i≥1）中的每个个体p，考察它所支配的个体集S_p，将S_p中的每个个体q的支配q的个体数量n_q减1，并计算个体q的累积排序值q_rank。如果支配q的个体数量n_q=0，则将q存入下一级非支配集F_i＋1。直到所有的个体排序完毕，算法中止。

2.交叉算子

在原始NSGA-Ⅱ算法中，实数编码的选择和交叉操作是分开的。为了从单目标交叉算子过渡到多目标中，将选择和交叉操作合并，具体的交叉算子描述如下：

第一步：初始化对角阵Γ=diag（γ₁，γ₂，…，γ_n），γ_i∈（－1，1）的随机数，且γ_i≠0，i=1，2，…，n。

第二步：从父代中随机选择两个个体xⁱ=（xⁱ₁，x₂ⁱ，…，xⁱ_n）T，x^j=（x^j₁，x^j₂，…，x^j_n）T。

第三步：产生一个随机数rnd，若rnd≤p_c（即不大于杂叉概率p_c）则进行以下杂交操作，产生后代个体y=（y₁，y₂，…，y_n）T：

式中，i_rank表示i的Pareto累积排序值。

若rnd＞p_c，则从个体i、j中选择Pareto累积排序值较小的作为后代，即

(www.xing528.com)

式中，i_rank表示i的Pareto累积排序值。

重复第二步、第三步，产生和父代种群规模大小一样的子代种群，并利用该种群进行变异操作。

上面这个选择和交叉操作结合的算子本身一方面以概率大小为1－p_c的概率保存了父代中的两两比较较优的个体（不参与交叉）；另一方面，在两两比较较优的个体附近搜索，提高了算法的收敛性，并且搜索范围也较SBX大，有助于提高结果的多样性，性能在理论上也较SBX好。从计算时间花费来说，因为选择算子和交叉算子结合在一起，减少了一半的数据存储时间。同时，也排除了主观交叉因子η_c的影响，使算法更符合进化规律。

3.变异算子

在上面在分析NSGA-Ⅱ的变异算子时，了解到NSGA-Ⅱ变异算子未充分利用精英解，也就未能充分地在精英解附近进行局部搜索。为了进一步改进算法的收敛性，结合单目标优化较好的变异算子，下面给出改进的变异算子。

第一步，生成n维标准正态分布的随机矢量c=（c₁，c₂，…，c_n）T，即c～（N（0，1），N（0，1），…，N（0，1））T；生成均值为0=（0，0，…，0）T，方差为σ²=（σ²₁，σ²₂，…，σ²_n）的n维正态分布Δν，即

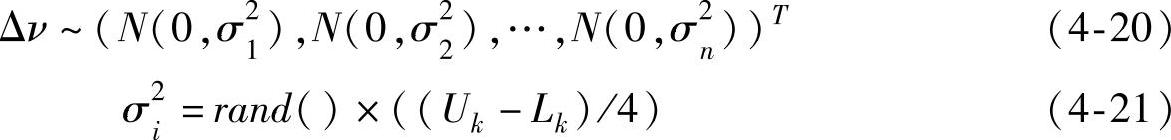
第二步，从父代精英解中随机选出一个，令其为best=（best₁，best₂，…，best_n）T

第三步，对满足best－y≥ε₁（ε₁=10^－4）的每个y=（y₁，y₂，…，y_n）T，•表示所有分量绝对值之和，即

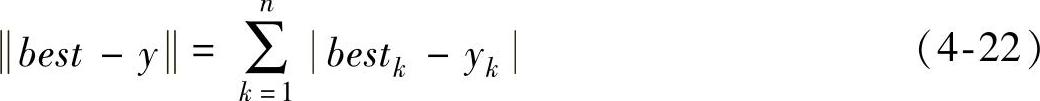
生成随机数r∈（0，1），若r＜p_m（p_m表示变异概率），则由下式产生变异后代z=（z₁，z₂，…，z_n）T，即

z=best＋V｜c｜ （4-23）

式中，V是对角矩阵，即V=diag（best₁－y₁，best₂－y₂，…，best_n－y_n）；对不满足best－y≥ε₁的每个y=（y₁，y₂，…，y_n）T，生成一个随机数r∈（0，1）。若r＜p_m，则由高斯变异，产生后代z=（z₁，z₂，…，z_n）T：

z=best＋Δν （4-24）

若r≥p_m，则z=y。

重复第三步，直到对经过交叉算子得到的子代种群的所有个体操作完成才得到父代种群P_t的子代种群Q_t，进而得到规模为2N的合并种群R_t=P_t∪Q_t，进而通过拥挤排序选择出下一代种群P_t＋1。

与NSGA-II的变异算子相比，由于使用了父代中的精英点，提高了精英点附近点的搜索效率，而且由于精英点在每一代的选择上是通过随机选择获取的，所以在整个G代的运算来看，又提高了最终结果的多样性。与此同时，排除了主观变异因子η_m的影响，使之更符合进化规律。