多目标优化：简介与优化方法

多目标优化问题是普遍存在的问题。为方便后面的描述，先做以下定义。

定义1（多目标优化问题）：一个通常的多目标问题包括一个含有n个参数（自变量）的集合，一个包含k个目标函数的集合和一个包含m个约束条件的集合。目标函数和约束条件都是自变量的函数。

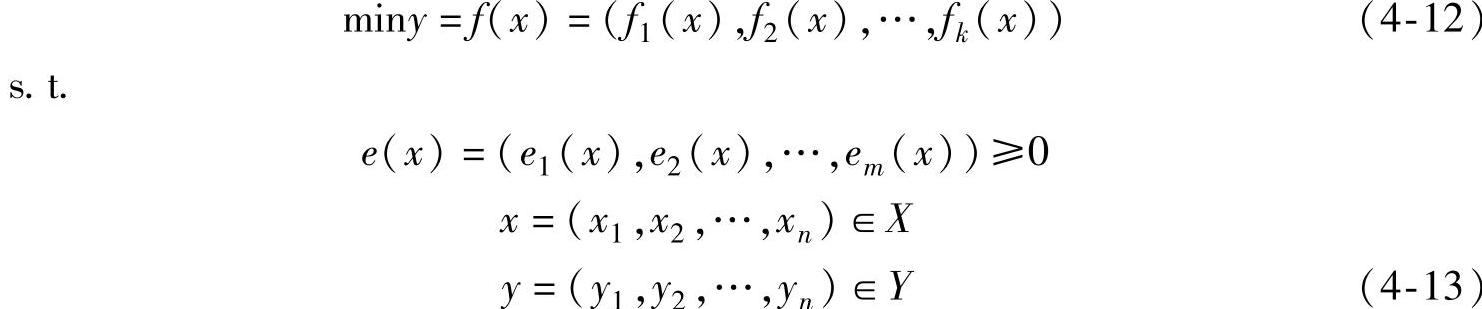
式中，x是自变量矢量；y是目标矢量，X是自变量空间；Y是目标空间；约束e（x）≥0确定了可行域。

定义2（可行集）：可行集X_f定义为自变量矢量x的集合，满足约束：

X_f={x∈X｜e（x）≥0} （4-14）

X_f的相是在目标空间的可行区域，可形式化表示为

Y_f=f（X_f）=U_x∈X_ff（x） （4-15）为不失一般性，这里我们只考虑最小化问题，对于最大化或混合的最大最小问题有着类似的定义。

假设两个目标函数一个是性能（Performance）的倒数（表示为f₁），另一个是开销（Cheapness）（表示为f₂），这两者都需要在尺寸大小约束（e₁）下被最大化。那么一种最优设计可能是既能够达到最优性能又能使开销最小并且没有违反尺寸大小约束的设计方案。如果存在这样的一个解，那么实际上解决的是一个单目标优化问题，即对于任意一个目标的最优解对另一个目标也是最优的。然而，多目标优化相应于不同目标函数的单独优化却是大不相同的，这正是多目标优化问题困难所在。因为这多个目标是相互冲突的，并且不能够被同时优化。相反，我们必须找到满意的折中解。因此，对于多目标优化问题，最优的概念需要重新定义。在单目标优化问题中，按照目标函数其可行集是全序的：对于两个解a，b∈X_f，或者f（a）≥f（b），或者f（b）≥f（a）。求解的目标是找到函数f（x）的最小值所对应的解。然而，当考虑几个目标的时候，情况又发生了变化：一般而言，X_f不是全序而是偏序的，这一点可以用图4-1解释。

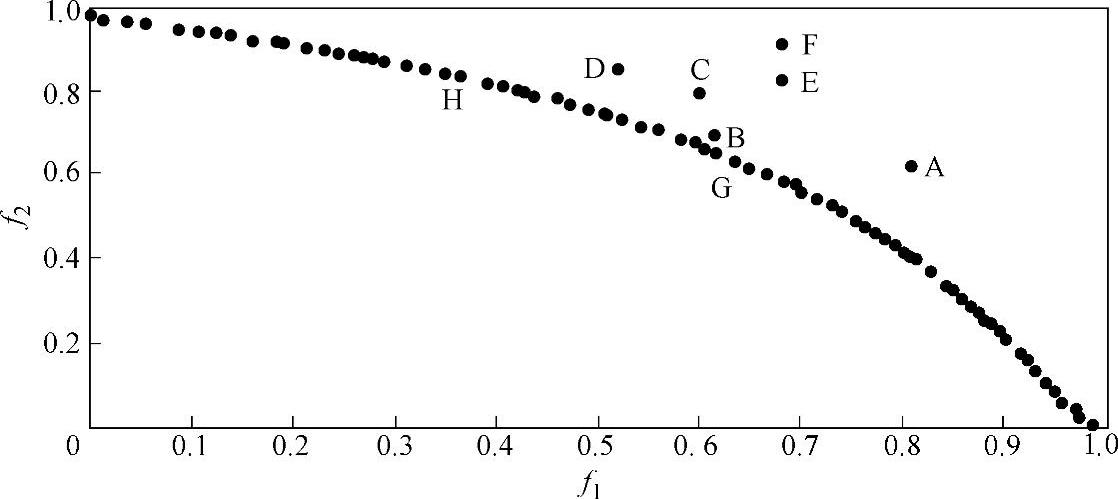
图4-1 偏序定义参考图

从图4-1很容易看出B点所代表的解优于E点所代表的解。如果仅仅是在一个目标上进行优化那是很容易的事情，例如B点和C点，尽管横轴所代表的目标相等，但B点比C点在纵轴所代表的目标上有更好的性能（值更小）。为了在数学形式上表达这种状态，大小关系=、≥、＞与单目标问题定义类似。下面把它们扩展到解决多目标优化问题的矢量形式中。

定义3：对于任意两个目标矢量u和v：

u=v，当且仅当u_i=v_i，i=1，2，…，k，读作u与v相同；

u＜v，当且仅当u_i＜v_i，i=1，2，…，k，读作u优于v；

u≤v，当且仅当u_i≤v_i，i=1，2，…，k，且∃j∈{1，2，…，k}，u_j＜v_j，读作u不劣于v，或v不优于u；(www.xing528.com)

u＞v，当且仅当u_i＞v_i，i=1，2，…，k，读作u劣于v；

u≥v，当且仅当u_i≥v_i，i=1，2，…，k，且∃j∈{1，2，…，k}，u_j＞v_j，读作u不优于v，或v不劣于u；

在这种定义意义下，图4-1中点的关系：B＜E，B＜C。然而当我们比较A和C或G和H时，我们不能说哪一个更优，因为A和C与G和H这两对无法比较。对于A和C，尽管A的纵轴所关联的量更廉价，但是它的横轴所关联的量要比C所关联的量大。因此，在多目标优化问题中，按照≥关系，自变量矢量a，b有三种可能的关系：f（a）≥f（b），f（b）≥f（a），f（a）！≥f（b）∧f（b）！≥f（a）。在这里，我们使用下面的符号和术语来区分不同的情况。

定义4（Pareto Dominance）：对于任意两个自变量矢量a和b，有

a≻b（a dominates b）if f（a）＜f（b）；

a≻－b（a weakly dominates b）if f（a）≤f（b）；

a～b（a is indifferent to b）if f（a）！≥f（b）∧f（b）！≥f（a）；

需要注意的是，定义4适用于无约束优化问题。对于有约束优化问题，相应的a支配b只需满足下面三个条件中的一个：

1）a在可行域中，而b不在可行域中；

2）a和b均不在可行域中，但a较b有较小的偏离可行域；

3）a和b均在可行域中，但a支配b。

这样定义后，通过非劣分类排序值，就可以将有约束优化问题直接转化为无约束优化问题。

基于偏序的概念，我们引出了多目标优化问题的最优标准。仍然参考图4-1，在A、B、C、D、E、F之间B点是最优的。它相应的自变量矢量x₀没有被任何其他的自变量矢量所支配。这也就意味着在某种意义上x₀是最优的，在任何一个目标上它都不能被其他个体支配。这些解被称为Pareto最优解，有时也称作非劣最优解。

定义5（Pareto Optimality）：一个自变量矢量x∈X_f，考虑X_f的一个子集A，如果∃a∈A，a≻x，则x被称作是对应于集合A的Pareto最优。

Pareto最优解的全体被称作Pareto最优解集；相应的目标矢量构成了Pareto最优阵面。Pareto最优解集构成了全局最优解集。然而，与单目标优化问题一样也存在局部最优，在某个邻域范围内，多个局部最优解构成了未被支配解集。这个概念是与Deb［5］所提出的全局和局部Pareto最优相对应的。