牵伸区内纤维运动和变速点分布探析

纤维在牵伸区的运动是由慢速转变为快速，每一根纤维都有一个变速的位置，称为变速点，此时快、慢速纤维间产生了相互位移，牵伸作用产生。由前面讨论可知，决定纤维变速的条件是作用在纤维上的引导力与控制力的大小，而影响此二力的因素较多，且带有一定的随机性，致使牵伸过程比较复杂。

因此，需要做一些假设和简化，通过理想牵伸的讨论来揭示实际牵伸的基本规律。

（一）理想牵伸

所谓理想牵伸有两方面的假设：一是喂入理想状态须条，即须条中纤维均平行、伸直、等长；二是纤维在牵伸区的同一个位置变速，可以是前钳口，也可以是牵伸区中的某一位置。

设在牵伸区须条中的两根纤维分别为A 和B，图6-10 所示为其在原须条中的排列位置，若两者之间的头端距离为a0，这个距离称为这两根纤维的头端“移距”，当纤维A 的头端到达前钳口时则A 变速，即以前罗拉速度V1 快速运动，而此时纤维B 仍然以后罗拉速度V2 慢速运动，于是A、B 两根纤维发生相对运动，移距开始变化。而当纤维B 经过t 时间到达前钳口时，也转变为快速V1，两纤维间不再有相对运动，此时A、B 两根纤维头端移距为a。在时间t 内，A 纤维移动的距离为a，B 纤维移动的距离为a0，则有：

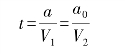
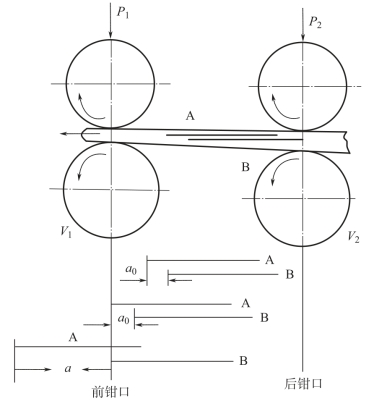
图6-10　理想牵伸时纤维的头端移距

牵伸后A、B 两根纤维的头端移距a 为：

式中：E——牵伸倍数；

　　　a0、a——牵伸前、牵伸后纤维头端的移距。

式（6-8）表明，须条中任意两根纤维间的距离，通过理想牵伸E 倍后也增大了E 倍，即纤维沿须条轴向产生了E 倍的相对位移，使纤维分布在更长的长度上，但不会产生附加的不匀。

（二）实际牵伸

事实上，喂入牵伸区的须条并非理想状态，而是不均匀的，单位长度的重量随时间而变化，纤维长度不相等，也不完全平行伸直。这种状态的须条进入牵伸区后，须条内纤维所受的引导力与控制力也会随之波动，直接影响浮游纤维的运动与变速，致使变速点变化。

因此，牵伸过程中纤维均在前罗拉钳口（或牵伸区内某一截面上）变速，这一假设与实际情况不符，实际上大部分纤维的变速点均不在同一个位置（截面）。纤维头端在不同位置变速时的实际牵伸情况如图6-11 所示。

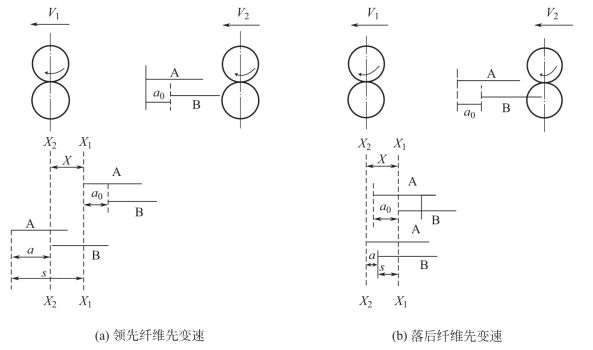
图6-11　纤维头端在不同位置变速时的牵伸

图中：a0 为牵伸须条中任意两根纤维A、B 变速前的头端距离；X1—X1、X2—X2 （前钳口线）为纤维的变速位置；X 为变速点间的距离

1.当领先的纤维先变速 即A 在X1—X1 截面由原来的慢速V2 变成快速V1，B 纤维经过t时间后，到达X2—X2 截面才由慢速V2 变成快速V1，此时，纤维A、B 头端的距离为a，也即牵伸后的头端距离（移距），计算如下。

A 到达变速点后，B 到达其变速点X2—X2 所需的时间t 为：

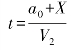
而在时间t 内，A 又由X1—X1 截面处向前运动了距离S，则：

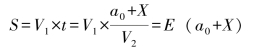
因此，A 与B 的距离变为：

2.当落后的纤维先变速 即B 在X1—X1 截面由慢速V2 变成快速V1，而A 经过t 时间后，到达X2—X2 截面也由慢速变成快速，此时，两者的头端距离可以计算如下：

B 到达变速点后，A 到达其变速点X2—X2 所需的时间t 为：

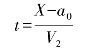
而在t 时间内，B 又由X1—X1 向前运动了距离S，则：

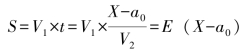
因此，A 与B 的距离变为：(www.xing528.com)

综合上述两种情况，任意两根初始头端距离为a0 的纤维，牵伸后产生新的移距a 可用下式表示：

式中：Ea0——E 倍牵伸时的理想移距；

　　　±X （E-1）——牵伸过程中，纤维头端在不同截面变速时引起的移距偏差；

　　　X——变速点间的距离。

式（6-9）表明，牵伸倍数越大，移距偏差越大，纤维在牵伸区内变速点间的距离越大，移距偏差越大。当移距偏差为“正”时，表示领先的纤维先变速，牵伸后纤维的头端移距比理想牵伸时大，表示牵伸后的须条比正常值细；反之，当移距偏差为“负”时，表示落后的纤维先变速，则牵伸后纤维的头端移距比理想牵伸时有所缩小，表示牵伸后的须条比正常值粗。移距偏差揭示了实际牵伸过程中须条产生不匀的原因，由牵伸产生的不匀称为牵伸不匀，是一种附加不匀。

（三）纤维变速点分布

由于罗拉钳口间的距离大于纤维长度，因此，每根纤维总有一浮游过程。当任意纤维的尾端离开后钳口开始浮游时，其接触慢速纤维的平均概率总是大于接触快速纤维的概率，此时控制力大于引导力，故在牵伸区的中后部（靠近后钳口处）保持慢速运动；之后，随着该纤维向前运动，其接触的慢速纤维减少，快速纤维逐渐增加，纤维的头端越接近前钳口，这种变速的可能性越大。纤维在牵伸区中的受力和运动状态的变化，使其在牵伸过程头端变速的位置不同，自变速点至前钳口形成一种分布，即为变速点分布，如图6-12 所示。

图中曲线1 表明，大部分纤维会在钳口附近集中变速，而一部分纤维的变速点距前钳口较远，即提前变速，使得这部分纤维变速点间的距离X 值增大，移距偏差增大，牵伸后须条的附加不匀增大。曲线2 的变速点更加集中且靠近前钳口，此时纤维变速点间的距离X 减小，移距偏差减小，牵伸不匀降低。而曲线3 正好相反。由此可见，降低牵伸不匀，必须使纤维变速点集中且靠近前钳口。

（四）影响纤维变速点分布的因素

牵伸区中摩擦力界的变化是影响纤维变速点分布的主要原因，而纤维长度、罗拉隔距、牵伸倍数等影响牵伸区的摩擦力界及其分布，进而影响纤维变速点的分布，可见纤维在牵伸区内变速的规律是比较复杂的。

为了进一步探讨影响纤维变速点分布的因素，可采用实验方法，变速点实验方法有示踪纤维（或示踪纱）法和间接测量法。前者是用记号纱条或嵌入有色纤维的纱条喂入牵伸装置，最后在输出产品上测量计算变速点分布曲线。后者采用模拟牵伸装置，并测出（或确定）纤维长度、线密度、牵伸倍数、隔距及牵伸区各有关断面的纤维根数，再借助纤维摩擦系数测定仪，用相关计算式进行统计计算，求出变速点分布曲线。

图6-13 为用间接测量法求得的变速点分布情况。结果表明：纤维长度越短，变速点分布越分散，纤维长度越长，变速点分布越集中。同时，采用的隔距小，纤维的变速点靠近前钳口，且较集中；隔距大时，变速点比较分散。

图6-14 为牵伸倍数和罗拉隔距不同时变速点分布情况。结果表明，当输出须条的纤维根数不变，只改变牵伸倍数时，牵伸倍数越大，意味着喂入须条数量增加，纤维变速点分布越分散，且变速点越远离前钳口。同样，当隔距增大时，纤维变速点分布越分散，但此时牵伸倍数的影响不明显。

由以上实验可知：

（1）随着纤维向前钳口靠近，按前罗拉速度运动的纤维数量逐渐增加，但开始时增加比较缓慢，然后转变为急剧上升，在靠近前钳口处，纤维几乎全部变为快速纤维。

（2）长度相同或整齐度好的纤维变速位置也不是相同的，而是形成一种分布；长度整齐度较差的纤维（棉纤维），其中短纤维变速比长纤维早、变速位置距离前钳口较远，而长纤维的变速位置靠近前钳口；在牵伸区的各个截面上，变速纤维中短纤维频率常高于长纤维频率，因此，短纤维是控制的主要对象。

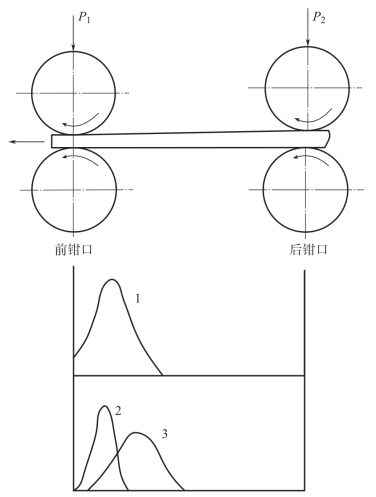
图6-12　简单罗拉牵伸区内纤维的变速点分布

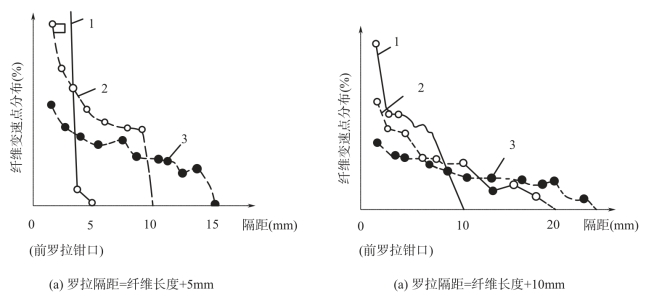
图6-13　纤维长度与罗拉隔距不同时纤维变速点分布

1—腈纶（76mm、3.3dtex） 2—腈纶（51mm、2.2dtex） 3—棉（品质长度30mm、1.4dtex）

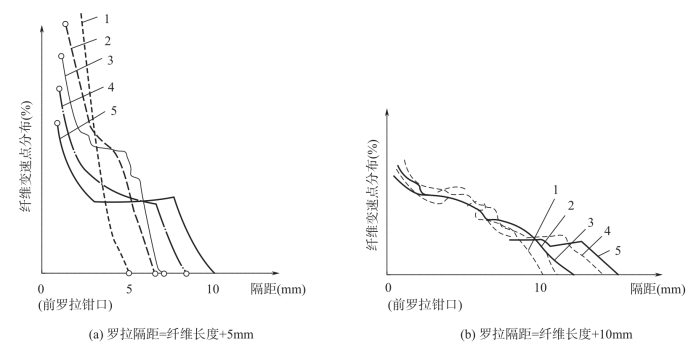
图6-14　牵伸倍数和罗拉隔距不同时变速点分布

1—后罗拉握持600 根纤维（6 倍牵伸） 2—后罗拉握持800 根纤维（8 倍牵伸） 3—后罗拉握持1000 根纤维（10 倍牵伸） 4—后罗拉握持1200 根纤维（12 牵伸） 5—后罗拉握持1400 根纤维（14 牵伸）

（3）当牵伸倍数一定时，随牵伸区隔距增加，变速点分布的离散性增加，变速点远离前钳口。在隔距相同时，随着牵伸倍数的增加，变速点分布的离散性越大，且变速点离前钳口越远。

（4）实验中还发现，绝大多数纤维在某一截面上瞬时地改变为前罗拉速度后，一直按前罗拉速度运动。但少数纤维，主要是部分短纤维，瞬时完成变速后，还会在牵伸区中多次改变速度。也有极少数纤维的加速过程较长，在此时间内出现了中间速度。甚至某些长度很长的纤维在加速过程中有时出现负速运动现象，这是由于须条中纤维存在弯钩所引起的。

（5）此外，实验采用不同形式的牵伸装置时，简单的由两对罗拉组成的牵伸装置，纤维变速点分布最离散，而且距前钳口最远，输出须条的条干均匀度最差。

综上，纤维运动状态的多变反映了纤维头端变速点分布的离散情况。为了尽可能减小牵伸产生的不匀，应控制纤维在牵伸区的运动，使头端变速点分布尽可能集中，并对时间稳定。由移距偏差X （E-1）可知，随着牵伸倍数E 的增大，移距偏差增大，应尽可能减小X，使其趋于零，使移距偏差减小，降低牵伸不匀。

实践中是通过合理布置牵伸区内摩擦力界的分布，来控制纤维的运动和变速的，使纤维变速点分布满足牵伸要求。