如何计算短路电流？

短路指载流导体相与相之间发生非正常接通，在中性点直接接地的系统中还有各相与地之间的短路。电气设备在短路时应能承受动稳定和热稳定。计算短路电流和校验电气设备是非常重要的。

相关知识

一、短路原因、种类

1.短路原因

形成短路的原因很多，主要有以下几个方面：

（1）元件损坏，例如设备绝缘材料老化，设计、制造、安装及维护不良等造成的设备缺陷发展成短路；

（2）气象条件恶化，例如雷击过电压造成的闪络放电，由于风灾引起架空线断线或导线覆冰引起电杆倒塌等；

（3）人为过失，例如运行人员带负荷拉刀闸，检修线路或设备时未排除接地线就合闸供配电等；

（4）其他原因，例如挖沟损伤电缆，鸟兽、风筝跨接在载流裸导体上等。

2.短路种类

在供配电系统中危害最大的故障就是短路。在三相系统中，短路的基本形式有：三相短路、两相短路、单相短路以及两相接地短路。各种短路示意图如表5－1所示。

表5－1　各种短路示意图

当三相短路时，由于短路回路阻抗相等，因此三相电流和电压仍是对称的，故又称为对称短路。而出现其他类型短路时，不仅每相电路中的电流和电压数值不等，其相角也不同，这些短路总称为不对称短路。

一般工业企业供配电系统都为小接地电流系统，并且离发电厂较远，所以两相短路电流和单相接地短路电流都比三相短路电流小。因此在计算短路时，以三相短路电流为重点进行计算。此外，研究三相短路之所以重要还由于在分析计算不对称短路时，经常利用对称分量法将不对称短路分解成三相对称的形式加以讨论。

3.计算短路电流的目的

计算短路电流的目的是解决以下几个方面的问题：

（1）正确选择和校验电气设备。电力系统中的电气设备在短路电流的电动力效应和热效应作用下，必须不受损坏，以免扩大事故范围，造成更大的损失。为此，在设计时必须校验所选择的电气设备的电动力稳定度和热稳定度，因此就需要计算发生短路时流过电气设备的短路电流。如果短路电流太大，必须采用限流措施；

（2）继电保护的设计和整定。关于电力系统中应配置什么样的继电保护，以及这些保护装置应如何整定，必须对电力网中可能发生的各种短路情况逐一加以计算分析，才能正确解决；

（3）电气主接线方案的确定。在设计电气主接线方案时往往出现这种情况：一个供配电可靠性高的接线方案，因为电的联系强，在发生故障时，短路电流太大以至必须选用昂贵的电气设备，而使所设计的方案在经济上不合理。这时若采取一些措施，例如适当改变电路的接法，增加限制短路电流的设备，或者限制某种运行方式的出现，就会得到既可靠又经济的主接线方案。总之，在评价和比较各种主接线方案选出最佳者时，计算短路电流是一项很重要的内容。

计算短路电流必需的原始资料：

应该了解变电所主接线系统，主要运行方式，各种变压器的型号、容量、有关各种参数；供配电线路的电压等级，架空线和电缆的型号，有关参数、距离；大型高压电机型号和有关参数，还必须到电力部门收集下列资料：

（1）电力系统现有总额定容量及远期的发展总额定容量；

（2）与本变电所电源进线所连接的上一级变电所母线，在最大运行方式下的短路电流，最小运行方式下的短路电流或短路容量；

（3）工厂附近有发电厂的应收集各种发电机组的型号、容量、次暂态电抗、连线方式、变压器容量和短路电压百分数，输电线路的电压等级，输电线型号和距离等；

（4）通常变电所有两条电源进线，一条运行，另一条备用，应判断哪条进线的短路电源较大，哪条较小，然后分别计算最大运行方式下和最小运行方式下的短路电流。

二、无限大容量电源系统供配电时短路过程

1.无限大容量电源系统定义

无限大容量电源系统，这个名称从概念上是不难理解的：

（1）电源容量为无限大时，外电路发生短路（一种扰动）所引起的功率改变对于电源来说是微不足道的，因而电源的电压和频率保持恒定；

（2）无限大容量电源系统可以看作是由无限多个有限功率电源并联而成，因而其内阻抗为零，电源电压保持恒定。

实际上，真正的无限大容量电源是没有的，而只能是一个相对的概念，往往是指其容量相对于用户供配电系统容量大得多的电力系统。如果系统阻抗（即等值电源内阻抗）不超过短路回路总阻抗的5%～10%，或电力系统容量超过用户供配电系统容量50 倍时，可将电力系统视为无限大容量系统。

对一般工厂供配电系统来说，由于工厂供配电系统的容量远比电力系统总容量小而阻抗又较电力系统大得多，因此工厂供配电系统内发生短路时，电力系统变电所馈电母线上的电压，几乎维持不变，也就是说可将电力系统视为无限大容量的电源。另外由于按无限大容量电源系统所计算得到的短路电流，是电气装置所通过的最大短路电流。因此，在初步估算装置通过的最大短路电流或缺乏必需的系统数据时，都可以认为短路回路所接的电源是无限大容量的电源系统。

2.无限大容量电源系统三相短路的物理过程

图5－1（a）是一个无限大容量电力系统发生三相短路时的电路图。由于三相对称，因此这一三相短路的电路可由图5－1（b）的等效单相电路图来分析。图中的Z＝RΣ＋jXΣ，为从电源到短路点的等值阻抗，U 为无限大电源的端电压，其内阻抗为零。当开关S 闭合时，相当于突然三相短路，因而短路的过渡过程将与R、L 电路接通正弦电压时的过渡过程相类似。

图5－1　无限大容量电力系统发生三相短路

（a）三相电路图；（b）等效单相电路图

根据电路理论，突然短路时电路的方程式为

式中 ik——短路电流的瞬时值；

θ——短路发生时的电源电压相位角；

Um——电源电压的幅值。

求解方程可得短路电流瞬时值为：

式中 Ipm——短路电流周期分量的幅值

Im——短路前负载电流的幅值；

φ——短路前负载电流的阻抗角；

φk——短路回路的阻抗角；

τ——短路回路的时间常数，

由上式可见，短路电流ik 由两部分组成，第一部分是短路电流的稳态分量，随时间按正弦规律变化的，所以又称周期分量。此分量是外加电压在阻抗的回路内强迫产生的，所以又称为强制分量，用ip 表示。第二部分为短路电流的暂态分量，是随时间按指数规律衰减的，并且偏于时间轴的一侧，称为非周期分量或自由分量，可用inp表示，所以整个过渡过程短路电流为：

产生非周期分量的原因在于电路中有电感存在。在短路的瞬间，回路中的电流由负载电流Imsin（θ－φ）突然增加到Ipmsin（θ－φk）。由于电感电路的电流不能突变，势必产生一个非周期分量电流来维持其原来的电流。它的初始值，即为周期分量初始值和短路瞬间负载电流之差，即：

非周期分量按指数规律衰减的快慢取决于短路回路的时间常数τ。对于高压电网来说，其电阻较电抗小得多，此时多取：τ＝0.05 s，而在计算大容量电力网或发电机附近短路时，τ 为0.1～0.2 s。如按τ＝0.05 s 考虑，在短路后的0.2 s 左右，非周期分量即可衰减完。

当非周期分量衰减完了，短路电流的暂态过程结束而进入短路的稳定状态，此时的短路电流，称为稳态短路电流或简称稳态值。

图5－2表示出无限大容量系统发生三相短路前后，电流、电压的变动曲线。由图可以看出短路电流在到达稳定值之前要经过一个暂态过程，这一暂态过程是短路非周期分量电流存在那段时间。短路非周期分量电流衰减完毕后（一般经t≈0.2 s），短路电流达到稳定状态。

图5－2　无限大容量系统发生三相短路前后，电流、电压的变动曲线

在电源电压及短路地点不变的情况下，要使短路全电流达到最大值，必须具备以下条件：

①短路前电路处于空载状态；

②短路发生在某相电压瞬时值过零值的时候，即当t＝0 时，初相角θ＝0°；

③短路回路近于纯感性电路，即φk ≈90°。

在实际供配电系统中出现上述情况的概率很小，但是它所引起的短路后果将是最严重的。因此，研究这种现象仍具有明显实际意义。顺便指出，上述结果是三相短路时其中的一相，并不是各相都会出现最严重的情况。只有在短路时，电压过零的那一相才会出现最严重的情况。另外还要指出，在实际短路发生后，并不能在电路中分别测出短路电流周期分量和非周期分量，实际测得的是两者叠加后完整的短路电流波形。引入周期分量和非周期分量的目的，仅仅是为了分析问题的方便和清晰。

3.短路计算的有关参数

次暂态短路电流I″。它是指短路瞬时，短路电流周期分量为最大幅值时所对应的有效值。

短路冲击电流ish。它是指短路全电流的最大瞬时值。由图5－2所示短路全电流的曲线可以看出，短路后经半个周期（约为0.01 s）达到最大值，此时的电流值即短路电流冲击值。短路电流冲击值可按下式计算：

式中 Ksh——短路电流冲击系数，I＜Ksh＜2。

一般在高压供配电系统中，通常取τ＝0.05 s，Ksh＝1.8，则ish＝2.55I″。在1 000 kV·A及以下的电力变压器二次侧及低压电路中发生三相短路时，一般可取Ksh＝1.3，因此ish＝1.84 I″。

Ish是短路冲击电流有效值。它是指短路后第一个周期的短路全电流有效值。

在高压供配电系统中，Ksh＝1.8 时，Ish＝1.51I″；在低压供配电系统中Ksh＝1.3 时，Ish＝1.09 I″。

I∞为短路稳态电流。它是指短路电流非周期分量衰减完毕以后的短路全电流的有效值。

从前述可知，无限大容量电源系统发生三相短路时，短路电流周期分量的幅值始终不变，则有：

三、无限大容量电源条件下短路电流的计算方法

1.一般规定

为了简化短路电流计算的方法，在保证计算精度的情况下，忽略一些次要因素的影响，作出如下规定：

①所有点的发电机相位角相同、电源的频率相同，短路前电力系统的电势和电流是对称的；

②认为变压器是理想变压器，变压器的铁芯始终处于不饱和状态，即电抗值不随电流大小发生变化；

③输电线路的分布电容略去不计；

④每一个电压级采用平均额定电压，这个规定在计算短路电流时，所造成误差很小。唯一例外的是电抗器，应采用加于电抗器端点的实际额定电压，因为电抗器的阻抗通常比其他元件阻抗大得多，否则误差偏大；

⑤用式计算高压系统短路电流时，一般只计算发电机、变压器、电抗器、线路等元件的电抗。因为这些元件X／3＞R 时，可略去电阻的影响，只有在短路点总电阻大于短路点总阻抗1／3 时，才加以考虑采用∣Z∑∣来代替X∑；

⑥短路点离同步调相机和同步电动机较近时，应考虑对短路电流值的影响；

⑦在简化系统阻抗时，距短路点远的电源与近的电源不能合并；

⑧以供配电电源为基准的电抗标幺值大于3，可认为电源容量为无限大的系统，短路电流的周期分量在短路全过程中保持不变。

2.标幺制的概念

短路电流计算常采用标幺制。所谓标幺制，就是将电压、电流、功率、阻抗等物理量不用其有名值表示，而用标幺值表示。标幺是这样得出的，将一个量与一个基准量相比较，并将该基准量作衡量单位：

显然，同一个实际值，当所选的基准值不同时标幺值也就不同。切记，说明一个物理量的标幺值时，必须说明其基准值为何，否则只说明一个标幺值是没有意义的。

标幺值一般又称为相对值，是一个无单位值，这里用带∗号的上标以示区别。标幺值乘100，即可得到用同一基准表示的百分值。

采用标幺制有如下的优点：

①应用标幺制易于比较电力系统各元件的特性及参数。电力系统中各种电气设备的额定电压的高低、容量的大小彼此相差很大。它们的特性和参数若用有名值表示时，也就差别很大，很难进行比较。但用标幺值表示后，这些特性和参数都在一定的范围内，就便于进行对比分析。例如，一台铭牌数据为110 kV、10 000 kV·A的变压器，其短路电压为Uk1＝11.6 kV，而一台铭牌数据为10.5 kV、7 500 kV·A的变压器，其短路电压为Uk2＝1.05 kV，这两个短路电压值相差很大，不好比较，如果都取它们各自的额定电压作为基准，则其标幺值为：

以上两式说明，它们的短路电压都是其额定电压的10 %左右。

②采用标幺制便于判断电气设备的特性和参数的优劣。例如，设已知一台发电机运行中，其端电压为10.5 kV，相电流为1 000 A，从这些数值不能立刻判定运行情况是否正常，但如果得到的数据是以发电机额定值作为基准的标幺值，当看到U∗＝1.0，I∗＝0.8，便立即可以断定发电机的运行电压是正常的，负载电流值小于额定电流值。可见，用标幺值表示比用实际值能给人以更明确的概念。

③应用标幺值可以使较复杂系统的计算工作大大简化。

3.电路各元件阻抗的计算

1）基准值计算

高压供配电系统通常采用标幺值的计算方法来计算短路电流，所以应求出供配电系统中各元件的电抗标幺值。

采用标幺制计算时，首先必须选定基准值。原则上说基准值可以随便选择，通常可以选该设备的额定值作为基准值或整个系统选取便于计算的共同基准值。但是，并不是所有量的基准值都可以随便选定。在电路计算中，各量基准值之间必须服从电路的欧姆定律和功率方程式。也就是说在三相电路中，电流、电压、阻抗和功率这四个物理量的基准值之间应当满足下列关系式：

式中 Ud、Id、Sd、Zd——分别为电压、电流、功率、阻抗的基准值。

显然，只要选定其中两个量的基准值，其余两个基准值也就确定了。实际计算短路电流时，一般均首先确定视在功率和电压的基准值Sd 及Ud。为了计算方便通常取基准容量Sd＝100 MV·A，基准电压Ud 一般取用各级电网的平均额定电压。当基准容量和基准电压选定以后，则电流和阻抗的基准值分别为：

2）元件标幺值的计算

在选定和求出各量的基准值后，就可以很方便的求出其标幺值。对于不同变量计算公式如下。

在对称三相电路中，无论是三角形还是星形接线，线电压和相电压、线电流和相电流、三相功率和单相功率的标幺值都是一样的，因此，在计算中可以按单相电路的标幺值来计算，这是标幺制算法的一大优点。

3）标幺值相互变换的方法

在电力系统的实际计算中，对于直接电气联系的网络，在制定标幺值的等值电路时，各元件的参数，必须按统一的基准值进行归算。然而，从手册或产品说明书中查得的电机和电器的阻抗值，一般都是以各自的额定容量（或额定电流）和额定电压为基准的标幺值。由于各元件的额定值可能不同，而基准值不相同的标幺值是不能直接进行加、减、乘、除等运算的。因此在制定等值电路计算短路电流之前，首先必须把不同基准值的阻抗换算成统一基准值的标幺值。换算方法如下：

①一般的情况下，基准电压都取各级的平均电压。而基准容量不同时，可将基准容量为Sd1的标幺值换算为基准容量为Sd2的标幺值，以电抗标幺值为例，其转换方法为：

②两个标幺值的基准容量和基准电压都不相同时，可按下式进行变换：

4）系统中各种元件的电抗标幺值

电力系统中往往具有许多不同电压级的线路段，通过升压或降压变压器连接在一起。用标幺值进行计算时，系统各元件阻抗的标幺值需归算到同一电压级，即归算到基本电压级。在选定基本电压级的基准电压之后，线路其他各段的阻抗在归算时应采用的基准电压，可根据该段线路与基本电压线路间所有变压器的变比，采用折算法用下式求出

式中 Ud——基本电压级的基准电压；

Ud（n）——计算元件阻抗标幺值时各线段应该采取的基准电压；

k1、k2、k3 …kn——各线段与基本电压级线路间所有变压器的变比。

根据式（5－14）和式（5－15），显然归算到基本电压级的某个线段的电抗标幺值为：

上述方法是根据变压器的实际变比计算不同电压级电网中各元件阻抗标幺值的精确计算法，它主要用在电力系统用计算机求解短路电流的计算中。目前，在工业企业供配电系统中，多采用近似计算法求解短路电流。所谓近似法，就是不管网络中变压器的实际变比为多少，而一律视为相应等级的平均额定电压的变比，即网络中各线段的电压均为相应等级的平均额定电压。现举例说明如下。

图5－3所示为三个电压级的电力网。

图5－3　短路回路阻抗计算图

当选取短路点所在的UavⅢ作为基本电压级，而将网络所有元件的电抗标幺值都按此基本电压级进行归算时，根据式（5－12）应有：

发电机：

同样可得：

变压器T1：

线路L1：

限流电抗器：

其他元件也可写出类似的式子，就不再一一论述。

从以上分析可知，当采用线路平均额定电压代替网络的实际电压后，各元件电抗基准标幺值只和基准功率Sd 以及元件所在网络的平均额定电压Uav有关，而和所设的基本电压Ud 无关。

实践证明用线路平均额定电压代替网络的实际电压的假定并不会增大计算误差，却使计算大大简化。而且同一电路不同点短路时，只要Sd 不变，各元件的基准电抗标幺值也是不变的。为了使用方便，根据上述标幺值的定义和归算原则，将各种元件的标幺值，及有名值的变换公式汇总如表5－2所示。

表5－2　电抗标幺值和有名值的变换公式

［例5－1］ 某供配电系统的计算电路图如图5－4（a）所示，试用标幺值计算k1 点和k2 点的短路回路总阻抗。

图5－4　某供配电系统的计算电路图

（a）计算电路图；（b）等值电路图

［解］

首先作出等值电路图如图5－4（b）所示。设Sd＝100 MV·A，计算各元件的电抗标幺值：

k1 点的短路回路总阻抗为：

k2 点的短路回路总阻抗为：

4.无限大容量电源条件下三相短路电流的计算

计算步骤如下所述。

（1）按照供配电系统图绘制等效电路图，要求在图上标出各元件的参数，对复杂的供配电系统，还要绘制出简化的等效图。

（2）选定基准容量和基准电压，按照公式求出基准电流和基准电抗。

（3）求出供配电系统中各元件电抗标幺值。

（4）求出由电源至短路点的总阻抗。

（5）按下式求出短路电流标幺值。

由于电源是无限大容量，所以，短路电流周期分量保持不变，即：

（6）求出短路电流和短路容量。

（7）求出稳态短路电流I∞和稳态短路容量S∞。

（8）求出短路冲击电流ish 和短路全电流最大有效值Ish。

［例5－2］ 无限大容量系统通过一条70 km 的110 kV 输电线路向某变电所供配电，接线情况如图5－5所示。试分别用有名单位制和标幺值计算输电线路末端和变电所出线上发生三相短路时，短路电流周期分量的有效值和冲击短路电流。

图5－5　接线图

［解］

首先选取功率基准值Sd＝15 MV·A，电压基准值Ud＝U。

（1）k1 点短路时，线路L1 的电抗标幺值为：

化成有效值为：

（2）k2 点短路时，线路L1 的电抗标幺值为：

变压器T 的电抗标幺值为：

三台变压器并列运行时电抗的标幺值为：

化成有效值：

冲击短路电流为：

四、有限容量电源系统的三相短路电流计算方法

1.有限容量电源供配电系统三相短路的过渡过程

电源为有限容量时，电源的阻抗就不能忽略。在短路过程中，由于短路回路阻抗减少，短路电流必然增大造成电源端电压下降，使短路电流周期分量产生衰减。当发生短路的网络电源容量较小，或短路处靠近电源时，都应视为有限容量电源系统的短路情况，不能再用上节中所述的方法来计算短路电流，而必须考虑到突然短路时发电机内部的电磁暂态过程，才能得出正确的计算结果。

当发电机定子回路发生三相短路时，由于阻抗突然减少，产生很大的近似纯感性的短路电流。同时，在定子回路中，随之产生一个很大磁通Φ，其方向和正常时的励磁磁通相反，形成去磁作用，如图5－6所示。根据磁链不能突变的原则，转子里的励磁绕组和阻尼绕组都将感应出电动势，并分别流出有自由分量的电流ifk和idk，同时又分别产生磁通Φfk和Φdk使短路瞬间两侧磁通大小相等，即Φ＝Φfk＋Φdk，且方向相反，以维持发电机气隙间的总磁通不变。所以，短路瞬间发电机的电动势并不变，但励磁绕组和阻尼绕组中的自由分量电流ifk和idk，无恒定电源维持，势必按指数规律衰减。随着励磁绕组和阻尼绕组中磁通迅速减少，短路电流所产生的去磁作用显著增加，则引起发电机的总磁通减少，使定子内的电势随之下降，短路电流的周期分量当然要随之下降。一般经过3～5 s 之后，转子中的自由分量电流衰减结束，使发电机进入短路后的稳定状态。

图5－6　发电机短路时磁通的关系图

以上分析并没有考虑发电机自动调节励磁装置的作用，即认为在整个短路过程中发电机的励磁电流不变，也就是感应电动势等于常数。实际上，在现代电力系统中，同步发电机一般都装有自动调节励磁装置，其作用是当发电机电压变动时，自动调节励磁电流，使发电机的端电压保持在规定的范围内，这种装置也称为自动电压调整器。当发电机外部发生突然短路时，短路电流引起的去磁作用，使发电机的端电压急剧下降，自动调节励磁装置中的强行励磁装置起作用，迅速增大励磁电流，以使发电机的端电压重新回升。但是，任何一种类型的自动调节励磁装置，由于调节装置本身的反应时间以及发电机本身的励磁绕组的电感作用，而不可能立即增大励磁电流，而是经过一段很短时间后才能起作用。因而，不论是否装设自动调节励磁装置，在短路瞬间以及短路后的几个周期内，短路电流的变化情况都是相同的。图5－7中所示分别为有自动调节励磁装置和无自动调节励磁装置的发电机在发生突然短路后短路电流的变化曲线。从图中可以看出，两者的区别在于：有自动调节励磁装置的发电机系统，在发生短路后，短路电流周期分量经过最初的下降之后，随着发电机电压的提升将逐渐增大而进入稳定状态，无自动调节励磁装置的发电机系统在短路后，短路电流的周期分量是一直下降而达到稳定状态。

图5－7　发电机短路电流变化曲线

（a）有自动调节励磁装置的发电机短路电流变化曲线；（b）没有自动调节励磁装置的发电机短路电流变化曲线

有限容量系统，无论是否装设自动调节励磁装置，发生三相短路时，产生最大短路电流的条件与无限大容量系统是一样的，即短路电流的最大瞬时值出现在短路后0.01 s 的时候。

2.计算方法

工程上为简便计算，按I∗k1＝f（X∗N，t）的关系，绘成通用短路电流计算曲线，以供计算短路电流值查用。

计算步骤：

（1）按照供配电系统及各元件参数绘制计算系统图。

（2）选取基准值。

（3）求出各元件的电抗标幺值。

（4）求出各短路点的总电抗标幺值X∗∑。

（5）当所选取的基准容量与电源的总额定容量不相等时，必须将总电抗标幺值转换成以电源总额定容量为基准的计算电抗X∗∑′：

（6）根据计算电抗数值，去查与电源相对应的计算曲线便可查出不同时间的短路电流周期分量标幺值。

各种电源的计算曲线如图5－8～图5－13所示。

图5－8　具有自动调压调整器的标准型汽轮发电机的计算曲线

图5－9　没有自动电压调整器的标准型汽轮发电机的计算曲线

图5－10　具有自动调压调整器的标准型水轮发电机的计算曲线

图5－11　没有自动电压调整器的标准型水轮发电机的计算曲线

图5－12　没有自动调压调整器的发电机的平均计算曲线

图5－13　具有自动电压调整器的发电机的平均计算曲线

在计算曲线中只画到X∗＝3，如果X∗＞3，则不必去查曲线，可按电源为无限容量直接计算。

在计算曲线不容易查准确的地方可用表5－3～表5－6查得，如果算出的总计算电抗与表中的数值不符，可用插值法求出短路电流周期分量标幺值。

于是所求时间t 时的短路电流周期分量有效值为：

式中 IN∑——归算到计算点所在电压以及发电机总容量下的额定电流总和，即：

表5－3　汽轮发电机短路电流周期分量标幺值计算曲线

表5－4　水轮发电机短路电流周期分量标幺值计算曲线数值

续表

表5－5　汽轮发电机和水轮发电机短路电流周期分量标幺值计算曲线平均数值

续表

表5－6　各类元件电抗的平均值

［例5－3］ 某工厂供配电系统的计算电路如图5－14（a）所示，发电机为有自动调节励磁装置的汽轮发电机，各元件的参数均已标在图中，试求k1 点和k2 点三相短路电流的次暂态值、冲击值和稳态值。

图5－14

（a）计算电路图；（b）等值电路图

［解］

设Sd＝100 MV·A，Ud＝Uav。

1）求各元件电抗标幺值

电路如图5－14（b）所示。

其中：

2）求各点短路时的计算电抗

（1）k1 点短路时。

（2）k2 点短路时。

3）计算各点的短路电流

（1）k1 点。

由＝1.7 和t＝0 s，查图5－8曲线得＝0.604 则

对于稳态值可查t＝4 s 时的值，因为短路电流在t≥4 s 以后其过渡过程早已结束，而进入稳定状态。因此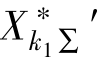，＝1.7 和t＝4 s 查图5－8曲线得：

则：

（2）k2 点，取Ud＝6.3 kV。

因为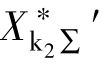≥3，可按无穷大容量系统处理，故：

或直接用下式计算：

五、低压电网中短路电流的计算

1.1 kV 以下的低压电网中短路电流的计算特点

（1）供配电电源可以看作是无限大容量系统。这是因为低压电网中降压变压器容量，远远小于高压电力系统的容量，所以降压变压器阻抗加上低压短回路阻抗远远大于电力系统的阻抗。在计算降压变压器低压侧短路电流时，一般不计电力系统到降压变压器高压侧的阻抗，而认为降压变压器高压侧的端电压保持不变。

（2）电阻值R 相对较大而电抗值X 相对较小，所以低压电网中电阻不能忽略，为避免复数运算，一般可用阻抗的模进行计算。

（3）直接使用有名值计算更方便。由于低压电网的电压往往只有一级而且在短路回路中除降压变压器外其他各元件的阻抗都用mΩ 表示，所以用有名值计算而不用标幺值计算。

（4）非周期分量衰减快。所以Ksh取1～1.3。

（5）必须计及下列元件阻抗的影响。

①长度为10～15 m 或更长的电缆和母线阻抗。

②多匝电流互感器原绕组的阻抗。

③低压自动空气开关过流线圈的阻抗。

④闸刀开关和自动开关的触点电阻。

2.计算方法

1）高压侧系统阻抗计算

高压侧系统电抗Xs 为：

式中 Xs——系统电抗，mΩ；

Ud——基准电压，V；

Ik——短路电流，kA

Sk——短路容量，kV·A。

2）短路回路中各元件阻抗的计算

（1）变压器阻抗RT、XT 分别为：

式中 RT、XT——分别为变压器绕组电阻和电抗，mΩ；

ΔPk——变压器短路损耗，kW；(www.xing528.com)

I2 NT——变压器二次侧额定电流，kA；

U2NT——变压器二次侧额定电压，V；

SNT——变压器额定容量，kV·A；

X∗T——变压器绕组电抗标幺值，

（Uk%为变压器电路电压的百分值）。

（2）母线电阻为：

3.短路电流计算

在1 000 V 以下的低压电网中，三相短路电流最大，两相短路电流较小。短路回路的总电阻为∑R，短路回路的总电抗为∑X。短路回路的电流值为：

式中 Ik（3）——三相短路电流，kA；

I″——次暂态短路电流，kA；

ish——冲击短路电流，kA；

Ish——三相短路电流第一周期全电流有效值，kA；

UC——计算电压，V；

∑R、∑X——分别为短路回路总电阻和总阻抗，mΩ；

Ksh——冲击系数（一般可取Ksh＝1.3）。

两相短路电流和三相短路电流的关系为：

［例5－4］ 试求图5－15计算电路图中d 点的三相短路电流。

图5－15　计算电路图

［解］

（1）系统电抗

（2）变压器阻抗

（3）母线阻抗

根据母线电抗计算公式：

（其中：a 为相间距离，h 为矩形母线的高度，D＝1.26a）

（4）自动开关线圈阻抗及触头的接触电阻

（5）刀开关触点的接触电阻

（6）电流互感器组

不计及电流互感器阻抗时，则短路电流的总阻抗为：

（7）三相短路电流

六、不对称短路电流的计算方法

1.对称分量法

在电力系统中，除了三相短路之外，还有不对称短路，例如单相短路、两相短路、两相短路接地等。而且根据运行经验，发生不对称短路的概率比对称短路多得多，据统计约占全部短路故障的90%以上。因此需要掌握不对称短路的分析法。

发生不对称短路时，电力系统的三相电流和电压是不对称的，因此，不能直接采用计算三相短路电流的方法来进行分析计算。不对称短路通常采用对称分量法进行计算。

对称分量法是将一个不对称的三相电流或电压系统分解成三个对称的电流或电压系统（正序、负序、零序），对分解所得的每个对称系统（正序、负序、零序），就可以用前述的分析对称电路的方法进行分析计算。

在对称分量法计算中，为了简化计算，引用一个专用的运算符号a，它是一个复数，其模为1，辐角是120°。即

如果为三相不对称的电压，以带下标1、2、0 的量分别表示各相电压的正序、负序和零序的对称分量，应用叠加原理可得：

解上式可以得到A 相正序、负序、零序的对称分量电压表达式为：

同样，三相不对称电流和它们的正序、负序、零序对称分量电流之间，也具有相同的形式。

应用对称分量法需满足两个条件：

①对称分量法是以叠加原理为根据的，所以只有当系统的参数是线性时才可应用；

②对称分量法适用于原来三相阻抗对称，而只有故障点处发生三相不对称短路的电路，否则问题往往不能得到简化。

最后还要指出：对称分量不仅是经过公式推导而得到的一种纯数学的抽象的概念，而且是客观存在的，即实测可得的。同时，每个分量分别还都有其单独的物理意义。因此，对称分量也常被应用于继电保护装置，如负序电压保护和零序、负序电流保护等。

2.不对称短路的序网络图

当电力系统的某一点发生不对称故障时，三相系统的对称条件将受到破坏。但这种对称条件的破坏是局部性的，即除了在故障点出现某种不对称之外，电力系统的其他部分仍是对称的。因而可以应用对称分量法，将故障处的电压、电流分解为正序、负序和零序三组对称分量系统。由于电路的其余部分是三相对称的，所以各序分量都具有独立性，从而可以形成独立的三个序网络。各序网络既然是对称的，就可以用一相来分析，用单线图来表示。图5－16为一个三相系统发生不对称短路时各序网络示意图，图中分别为k 点的三相不对称电压经变换后的正序、负序与零序电压Xl、X2、X0 表示系统中各序电抗的等效值。

1）正序网络

正序网络就是前面用来计算对称三相短路时的网络，流过正序点的全部元件的电抗均用正序电抗，如图5－16（a）所示。由于电源发电机的电势是正序电势，所以应包括于正序网络中，即正序网络是有源网络。正序网的电压方程为：

图5－16　序网络图

（a）正序网络；（b）负序网络；（c）零序网络

2）负序网络

负序电流和正序电流，在网络中所流经的元件相同，即组成负序网络的元件，与正序网络完全一样，不同点在于各元件的电抗应为负序电抗，发电机的负序电势为零，如图5－16（b）所示，所以负序网络是仅有负序电压的一个无源网络，其电压方程为：

3）零序网络

零序网络也是一个无源网络，电源发电机不存在零序电势，各元件的电抗应为零序电抗，如图5－16（c）所示，其电压方程为：

三相零序电流大小相等、方向相同，是一个流经三相电路的单相电流，只能经过大地（或公共接地零线）流动；如果是中性点不接地电力网（或没有公共接地零线），就不会出现零序电流。对于有零序电流通过，而又连在发电机或变压器中性点的消弧线圈等，由于它们所通过的零序电流为三相零序电流之和，即为一相零序电流的3倍，为使零序网络中这些元件上的电压降与实际电压降相符，必须将这些元件的阻抗乘以3。

如果将上述各序网络的基本公式加以汇总后可得到下列方程组：

3.各元件的各序电抗

1）正序阻抗

正序阻抗即各个元件在三相对称工作时的基波阻抗值，也就是在计算三相对称短路时所采用的阻抗值。

2）负序阻抗

电力系统中凡是静止的三相对称结构的设备，如架空线、电缆线、变压器、电抗器等，它们相与相之间的互感以及本身的自感与电流相序的改变无关，故这些元件的负序阻抗与正序阻抗相等。对于旋转的发电机和电动机元件，因定子和转子有相对运动，定子中负序电流所产生的旋转磁场，与转子旋转方向相反，所以，它们的负序电抗不同于正序电抗。发电机负序电抗平均值如表5－6所示。至于作为负荷主要成分的感应电动机，其负序电抗可近似地认为等于它的短路电抗对其额定容量的标幺值，其值在0.2～0.5 之间。因此，实际上综合电力负荷在额定情况下，负序电抗的标幺值取为0.35。

3）零序电抗

发电机、架空线路、电缆等元件零序电抗值如表5－6所示。

图5－17　各类变压器的零序等值电路

变压器的零序电抗决定于其绕组接法和结构。图5－17将一般常用的双绕组和三绕组变压器的零序等值电路，根据其连接组的类型综合列出，可供实际使用时参考。在具体应用图5－17来计算变压器的零序电抗时，应当按下列原则来处理：

①当铁芯结构为三相五柱式、三个单相组或壳式时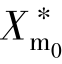，的值很大，可将励磁支路近似作为开路处理。同时，其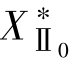，（若为三绕组变压器还有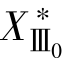）则与正序时基本相同；

②当采用三相三柱式铁芯时，，的值可近似等于正序电抗，但这时励磁支路不能作为开路处理；

③对Y／Y，Δ／Δ，Y／Δ连接的变压器，由于对外电路而言，零序电流均不可能流通，故其零序等值电路应作为开路处理，即X∗0＝∞；

④对Y0／Δ连接的变压器，若计及＝∞，则其（正序电抗）；

⑤对于某些连接方式而言，当不可能如Y0／Δ连接那样，将零序等值电路简单的归并为一个零序电抗值来代表，就应将变压器的零序等值电路纳入整个零序等值网络中去进行归并计算。

对于感应电动机，定子绕组接成Y 或Δ因此作为综合负荷的零序电抗在绘制系统的等效电路图时可不作考虑。

4.不对称短路的计算方法

用对称分量法求解不对称短路的基本步骤，可归纳如下：

①计算电力系统各元件的各序阻抗；

②根据故障的特征，作出针对故障点的各序网络图；

③由序网络图及故障的边界条件列出对应方程组作出相应的复合序网；

④按复合序网图或从联立方程组，解出故障点的电流和电压的各序分量，并将相应的各序分量相加，以求出故障点的各相电流和各相电压；

⑤计算各相序电流和各相序电压在网络中的分布，进一步求出各指定支路的各相序电流和指定节点的各相序电压。

下面分别介绍各种不对称故障的计算方法。

1）单相接地短路

图5－18所示为大电流接地系统，在k 点a 相发生接地故障。

a 相直接接地故障时，相当于在k 点接上一组不对称三相电抗；a 相对地的电抗为零，b、c 相对地电抗为无穷大，根据故障特征的条件可以写出以下三个关系式，即：

图5－18　单相直接接地

将式（5－45）转换成对称分量的关系，则为：

也就是说，在单相直接接地故障的情况下，以对称分量形式表示的三个关系式是：

式（5－46）称为单相直接接地故障的边界条件。此外根据式（5－44）有如下关系成立：

则可作出如图5－19的各序网络图。

图5－19

（a）正序网络；（b）负序网络；（c）零序网络

将式（5－46）和式（5－47）联立求解就可得出故障点的六个未知量：

另外，根据边界条件公式可以将图5－19的三个序网串联起来，如图5－20所示，称为单相直接接地的复合序网。这个复合序网也就是前述六个方程联解所对应的等值电路。

图5－20　单相直接接地的复合序网

从复合序网，可以很容易得出对称分量电流：

因此故障点a 相电流为：

将式（5－48）代入式（5－49）就可以求出故障点的对称分量电压再按照式（5－47）的关系，可得出故障点的各相电压

［例5－5］ 图5－21所示电力系统，发电机容量为1 000 kW，cos φ＝0.8，电压为400／230 V，x″d（x1）＝0.09，x2＝0.10，x0＝0.06。发电机中性点直接接地（xE＝0）。线路正序电抗为xWL1＝0.15，负序电抗为xWL2＝0.15，零序电抗为xWL0＝0.18.发电机电动势E″a＝1.0∠0°。求k1 点发生单相直接接地时的短路电流（以上标幺值都是以发电机额定容量和额定电压为基准）。

图5－21　接线图

［解］

X1∑＝x″d＋xWL1＝0.09＋0.15＝0.24

X2∑＝x2＋xWL2＝0.10＋0.15＝0.25

X0∑＝x0＋xWL0＝0.06＋0.18＝0.24

由式（5－48）、式（5－49）得：

短路电流为：

电流基准值：

所以有名值：Ia＝1.084×4.11＝7.414（kA）。

2）两相短路

图5－22所示简单电力系统在k 点发生b、c 两相短路。

两相直接短路时，相当于在k 点接上一组三相不对称阻抗；b、c 相之间的阻抗为0。根据故障条件写出关系式：

图5－22　两相直接短路

转换为对称分量得：

所以：

也就是说，两相直接短路的三个边界条件是：

将式（5－51）与式（5－44）联立求解就可求得k 点的电压和电流对称分量。

另外，根据边界条件式（5－51）可以得出两相直接短路的复合序网，如图5－23所示。

图5－23　两相直接短路的复合序网

从复合序网可得：

因此，短路电流为：

［例5－6］ 与例5－5 相同的电力系统，在k 点发生两相短路故障（b、c 相间短路），求短路电流。

［解］

从例5－5 已知：

由式（5－52）得：

由式（5－53）得：

电流基准值： Id＝1.804（kA）

故有名值： Ib＝Ic＝1.804×3.53＝6.37（kA）

3）两相直接短路接地的故障分析

如图5－24所示，电力系统在k 点发生b、c 两相直接短路接地故障。

图5－24　两相直接短路接地

两相直接短路接地相当于在k 点接上一组不对称阻抗：a 相对地阻抗无穷大，b、c 相对地阻抗为零。

根据故障条件得出关系式：

转换为对称分量关系得出：

所以两相直接短路接地的三个边界条件为：

将式（5－54）和式（5－55）联立求解就可求出故障点的对称分量电压和电流。

另外，根据边界条件可将三个序网并联得出两相直接短路接地故障的复合序网，如图5－25所示。

图5－25　两相直接短路接地的复合序网

从复合序网，可容易得出：

故障电流为：

将式（5－56）、式（5－57）和式（5－58）代入上式得：

同理可得：

将两相直接短路接地与三相直接短路相比较，可发现计算两相直接短路接地故障的正序电流时，其等值电路相当于在三相短路的等值电路中在短路点串入一个X2∑和X0∑并联的电抗值。

将式（5－55）、式（5－47）代入式（5－60）就可得出

5.正序等效定则

综合上面讨论的三种不对称短路电流的分析结果，可以看出，短路电流的正序分量计算公式可以统一写成：

式中 n——代表短路的类型；

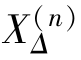——代表不同类型短路时的附加电抗。

式（5－61）表明，不对称短路时短路点正序电流值与在短路点串联一附加电抗，并在其后发生三相短路时的电流值相等，此关系称为正序等效定则。

同时根据上面分析结果可知，各种不对称短路时短路点故障相电流值与正序电流值成正比，可写成：

式中 m（n）——由短路类型（n）所决定的比例系数。

各种不对称短路时的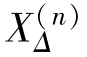与m（n） 值列于表5－7。

表5－7　各种短路时的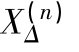与m（n） 值

七、电动机对短路电流的影响

在母线附近的大容量电动机正在运行时，在母线上发生三相短路，短路点电压立即降低，此时电动机将变为发电机运行状态，母线上电压将低于电动机的反电势。因此，电动机向母线的短路点馈送短路电流，成为一个附加电源。

1.同步电动机或同步调相机其附加短路电流值的计算

同步电动机处于过励磁状态下运行，并且总装机容量在100 MW 以上，而且在同步电动机近端同一点上发生三相短路，就构成附加电源。过励磁的同步电动机和调相机有单独的励磁绕组，其次暂态电势较大，向短路点馈送的短路电流时间较长，作用比较明显。

计算中应考虑的问题：

①同步电动机作为附加电源所供给的短路电流计算方法，与同步发电机相同，但是同步电动机的次暂态电抗与发电机不同，计算时应单独进行；

②由于同步电动机一般是凸极式的，所以其短路电流周期分量标幺值的计算曲线与有阻尼绕组、带自动电压调整器的水轮发电机的计算曲线相似，允许采用上述水轮发电机的计算曲线去查同步电动机提供的短路电流周期分量标幺值；

③由于同步电动机的时间常数T′与制作计算曲线时所采用的标准发电机的时间常数T相差较大，故不能用实际的时间t 去查曲线，而应当采用换算时间t′去查曲线：

制作曲线时，发电机标准时间常数T 的取值这样进行：对汽轮机取7 s，水轮机取5 s。对于同步电动机定子开路时，励磁绕组的时间常数平均值约为T′＝2.5 s，故有：

2.异步电动机反馈电流的作用

因为异步电动机没有单独的励磁绕组，当总装机容量在800 kW 以上，正在运行的高压电动机引出线发生三相短路，由于反电势作用时间较短，所以异步电动机反馈电流仅对短路电流冲击值有影响。

如果在异步电动机引出线处发生三相短路，异步电动机反馈冲击电流可按下式计算：

式中 ——异步电动机次暂态电势标幺值，一般取0.9；

——异步电动机次暂态电抗标幺值，一般取0.17；

KshM——异步电动机反馈电流冲击系数，一般取1.4～1.6；

INM——异步电动机的额定电流。

短路点总短路电流冲击值ish∑可按下式计算：

式中 ish——电源在短路回路提供的短路电流冲击值；

ishM——异步电动机反馈冲击电流值。

八、短路电流的热效应与力效应

1.短路电流的热效应

在线路发生短路时，由于短路后线路的保护装置很快动作，切除短路故障，所以短路电流通过导体的时间不长，通常不会超过2～3 s。但由于短路电流骤增很大，发出的热量来不及向周围介质散失，因此散失的热量可以不计，基本上看作是一个绝热过程。即导体通过短路电流时所产生的热量，全部用于使导体温度升高。

图5－26　导体的温度变化

式中 ik·t——短路全电流，ik·t＝iP·t＋inP·t；

ip·t、inP·t——分别为短路电流的周期分量和非周期分量；

QP——周期分量电流的热效应，kA2·s；

QnP——非周期分量电流的热效应，kA2·s。

即短路电流的热效应Qk 等于周期分量热效应QP 与非周期分量热效应QnP之和。

对热效应的计算，过去采用假想时间法，该法已不适合我国目前电力系统的情况，计算结果误差大。现在广泛使用实用计算法来计算，具体计算方法如下：

（1）周期分量热效应QP。

式中 I″——次暂态短路电流，kA；

秒时刻周期分量有效值，kA；

IP·t——t 秒时刻周期分量有效值，kA；

t——短路的持续时间，s。

为方便记忆，上面的近似计算公式可称其为“1－10－1”公式。

（2）非周期分量热效应QnP。

式中 T——非周期分量的等效时间，s。可由表5－8查得。

表5－8　非周期分量的等效时间

如果短路持续时间t＞1 s 时，导体的发热量主要由周期分量热效应决定。这时，可不计非周期分量热效应，即Qk≈QP。

根据短路电流的热效应Qk，可计算出导体在短路后所达到的最高温度，但这种计算，不仅相当烦琐，而且涉及一些难以准确确定的系数，包括导体的电导率（它在短路过程中不是一个常数），因此最后计算的结果，往往与实际出入很大。因此在工程计算中，一般是利用如图5－27所示曲线来确定，具体方法如下（参考图5－28）。

图5－27　用来确定θk 曲线

图5－28　由θL 查得相应曲线θk 的步骤说明

①在纵坐标轴上找出导体正常工作温度θL；

②由θ

L 查得相应曲线θk 上点a；

③由a 点查得横坐标轴上的KL；

④用下式计算Kk：

式中 S——导体的截面积。

⑤在横坐标轴上找出Kk；

⑥由Kk 查得相应曲线上的b 点；

⑦由b 点查得纵坐标轴上的θk 值。

如果所得值不超过最高允许温度，则表明载流导体能满足短路电流热稳定性的要求。

2.短路电流的力效应

供配电系统发生短路时，导体中将流过很大的短路冲击电流，从而产生很大的电动力，这时如果导体和它的支撑物的机械强度不够，必将造成变形或破坏而引起严重事故。为此，必须研究短路冲击电流所产生电动力的大小和特征，以便在选择电气设备时考虑它的影响，保证具有足够的稳定性，使电气设备可靠地运行。

对于两平行导体，通过电流分别为i1 和i2 时，两导体间的电动力为：

式中 i1、i2——两导体中电流瞬时值；

L——平行导体长度；

a——两导体的轴线间距离。

上式适用于圆形或管形导体，也适用于截面的周长尺寸远小于两根导体之间距离的矩形母线。如果两矩形截面平行导体相互距离很近，则其电动力需乘以形状系数KS。

形状系数KS 是的函数，可由图5－29查得。其中a、b、h 如图5－29中所示。当母线立放时，，其KS＜1；若母线平放时，，则KS＞1，但最大不超过1.4。如时，则有KS，近似等于1。

配电装置中导体均为三相，而且通常布置在同一平面内，当发生三相短路故障时，其中间相B 相导体的受力最大。三相短路电流iA、iB、iC 流经各相导体时，各相导体的受力情况如图5－30所示。

图5－29　矩形截面母线的形状系数曲线

图5－30　三相短路受力分析

中间相B 相导体受力为：

用三相短路冲击电流来表示其最大值为：

当发生两相短路时，电动力最大值为：

由于两相短路冲击电流，上式可用三相短路冲击电流表示为：

比较两式可知，三相线路发生三相短路时中间相导体所受的电动力，比两相短路时导体所受的电动力大。所以遇到求最大电动力时，应按式（5－71）。

任务实施

短路电流计算（表5－9）

表5－9　任务实施表

续表

评价总结

根据计算结果分析，进行评议总结，并填写成绩评议表（表5－10）。

表5－10　成绩评议表