正弦振荡电路的设计与调测实验优化

【实验目的】

(1)掌握RC和LC两种正弦振荡电路的设计和调测方法。

(2)加深对RC和LC两种振荡电路的理解和认识。

【设计任务】

(1)参考图8.8.4所示电路,设计一个具有自稳幅措施的文氏电桥RC正弦波振荡电路。

给定条件:

◆±12 V供电;

◆集成运放μA741。

指标要求:

◆振荡频率2 k Hz±5%;

◆输出幅度Uopp≥10 V;

◆波形无明显失真。

(2)参考图8.8.6所示电路,设计一个电容三端LC正弦波振荡电路并采用自生反偏压以稳定振荡幅度。

给定条件:

◆+12 V供电;

◆晶体管8050;

◆820μH电感;

◆其他元器件自选。

指标要求:

◆振荡输出频率250 k Hz±5%;

◆振荡输出幅度Uopp≥3 V;

◆波形无明显失真。

建议:

◆设置晶体管静态工作电流ICQ为1 m A左右。

【测试任务】

1.文氏电桥RC正弦波振荡电路的调测

(1)静态测试

◆电路规范连接电源。

◆检测运放μA741的2、3、4、6、7的直流电压是否正常。

(2)示波器观测振荡输出波形

◆分别判断振荡输出的频率和幅度是否符合指标要求。若不符合则调整电路元器件直至符合。

◆定量画出符合要求的振荡输出波形。

◆改变与二极管并联的电阻阻值,观察电路的输出变化,讨论二者之间的关系和相关原理。

2.LC正弦波振荡电路的调测

(1)静态测试

◆电路规范连接电源。

◆调整静态工作电流ICQ为设计值,检查晶体管直流偏压是否正常。

(2)示波器观测振荡输出波形

◆分别判断振荡输出的频率和幅度是否符合指标要求。若不符合则调整电路元器件直至符合。

◆定量画出符合要求的振荡输出波形。

(3)观察外界因素对振荡频率稳定度的影响

◆电源电压由+12 V逐渐减小至+8 V,观察不同电源电压时的波形变化,测出相应的振荡频率并计算频率稳定度。

◆电源电压为+12 V,电路正常振荡工作时用电热风或电烙铁隔空加热使晶体管温度升高,分别观测加热前和加热后的振荡频率变化情况并进行分析。

【提高要求】

将测试任务2中已经调测完毕的电路焊接到PCB上。

【实验预习】

(1)查阅相关器件数据手册,了解其特性和使用注意事项。

(2)阅读本实验【相关知识】,掌握相关电路的设计和调测方法。

(3)设计相关电路,列出详细设计过程并画出完整详细的电路图。对电路进行仿真和分析。

(4)针对测试任务拟定详细的调测操作步骤,设计相关数据表格,列出实验注意事项。

(5)在面包板上搭建实验电路。

(6)预习思考题:

①在RC振荡电路中,二极管稳幅效果和振荡波形的失真度之间存在怎样的关系?原理是什么?

②如何测量LC振荡器的静态工作电流ICQ?

③万用表如何判定LC振荡器是否起振?

【报告撰写】

实验之前

◆参考本书附录“实验报告格式”,结合实验预习过程完成报告1～5项。

实验之后

◆结合实验过程继续完成报告6～9项。

【相关知识】(www.xing528.com)

振荡电路按照能量转换原理的不同,分为反馈型和负阻型两大类。反馈型振荡电路的实质是具有正反馈的放大器。放大器通过正反馈电路将输出信号送回电路输入端,如果电路的放大倍数A和正反馈系数F满足AF>1,则电路在微小的扰动激励下,通过放大和反馈的不断循环使输出幅度不断增大,当大到一定的程度时由于某种原因使放大倍数和正反馈系数的乘积下降为AF=1,则电路输出将维持这一幅度不再变化,电路保持稳定振荡。电路这种在一定情况下使输出稳定的特性被称为电路的稳幅措施。

正弦波振荡电路除具有带正反馈的放大电路、具有稳幅措施外,还应具有选频功能,能将某一特定频率选出,使其成为唯一满足振荡条件AF≥1的频率,从而使振荡电路只能够输出此特定的单一频率的正弦信号。因此正弦波振荡电路必须包含选频网络。

根据构成选频网络的元件不同,正弦波振荡器有LC正弦波振荡器和RC正弦波振荡器两类。

LC正弦波振荡电路的选频网络由电感和电容构成,其振荡频率反比于LC乘积的平方根。如果LC振荡器工作于低频,选频网络的电容和电感的取值需要增大,从而导致元件体积和重量增加,所以LC振荡电路不适合工作在低频。通常的说法是LC振荡器用于1 MHz以上,RC振荡器用于1 MHz以下,但实际上二者频率的区分并没有这么绝对。

RC振荡电路的选频网络由电阻和电容构成,其振荡频率反比于选频网络中的RC乘积。如果RC振荡器工作于低频,增加的电阻不会导致元件体积和重量的增加,所以RC振荡器可以工作在低频。

1.RC正弦波振荡电路

RC正弦波振荡器有移相式、双T选频网络型、桥式等类型,其中桥式RC振荡电路结构简单便于调节,是常用的低频正弦波振荡电路,其基本电路形式如图8.8.1所示。

图8.8.1所示振荡器被也称为文氏电桥RC振荡器,其电路中R1和Rf引入电压串联负反馈使运放构成同相比例放大器,放大倍数为;而C1、C2、R2和R3组成正反馈电路,同时也是选频网络。为计算方便一般取等阻等容,即C1=C2=C,R2=R3=R′。该正反馈电路的反馈系数F为:

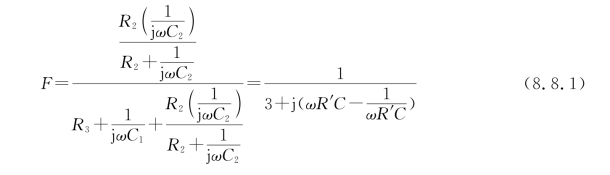
当时,上式中分母的虚部为零,取得最大值,同时相移为零。正反馈电路即选频网络的幅频和相频曲线如图8.8.2所示。被称为特征角频率,对应的特征频率为。电路工作时只有这个频率的信号满足相位平衡条件,因此电路的振荡频率为:

再根据起振条件AF>1,而,所以电路的放大倍数应有,即

Rf>2R1

实际上,电路在起振时满足Rf稍大于2R1即可,如果Rf过大,将降低选频特性,导致振荡输出波形失真严重。

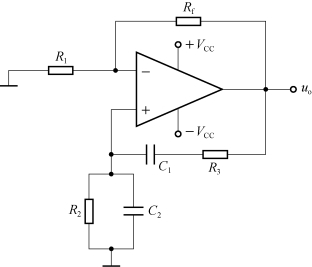
图8.8.1　桥式RC振荡电路

图8.8.2　选频网络的幅频和相频曲线

当电路起振后,随着振荡的继续,当输出信号幅度增加到一定程度时,应有稳幅措施使其保持稳定不再增加,即当输出信号幅度增加到一定程度时,应使振幅从AF>1回到AF=1,这一过程可以通过使Rf减小从而使A减小来实现。按照这一思路,Rf应为一个非线性电阻,如热敏电阻、晶体管等。常用的带有稳幅措施的文氏电桥RC振荡器如图8.8.3所示。

图8.8.3　带稳幅措施的文氏电桥振荡器

图8.8.3中两个方向不同的二极管和一个电阻并联作为电路的稳幅措施,利用二极管伏安特性的非线性,使振荡器的负反馈电阻Rf在输出信号幅度增加的过程中逐渐变小,负反馈增强,电压放大倍数降低,从而达到稳幅的目的。

改变与两个二极管并联的电阻以及电阻R的取值,可以调节二极管非线性电阻在Rf中的占比,非线性电阻占比大则稳幅效果好,但过大则会引起输出波形失真。一般与二极管并联的电阻取1～3kΩ,而R则用一个保护电阻和一个电位器串联代替,以方便调节。实用的文氏电桥振荡器如图8.8.4所示。

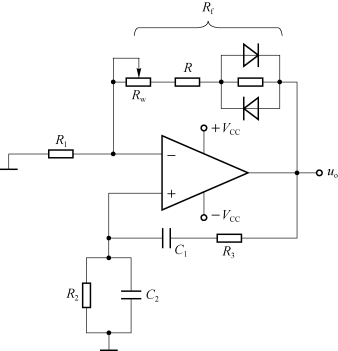
图8.8.4　实用的文氏电桥振荡器

2.LC正弦波振荡电路

LC正弦波振荡器按反馈电路的形式划分,有变压器反馈式、电感分压反馈式和电容分压反馈式。其中,电感分压反馈式或电容分压反馈式振荡电路中,分压的电感或电容支路的三个端分别是晶体管的三个极,所以被称为三点式振荡电路,其基本结构形式如图8.8.5所示。三个极之间的电抗分别用Xce、Xbe和Xcb表示。

如果要满足振荡的相位平衡条件,必须有:①Xce和Xbe符号相同;

②Xcb和Xce、Xbe符号相反。

如果Xce、Xbe是容抗,而Xcb是感抗,电路即为电容三点式;如果Xce、Xbe是感抗,而Xcb是容抗,电路即为电感三点式。Xce、Xbe和Xcb可以分别是单一的电抗元件电容或电感,也可以分别由不同的电抗元件组成,这样反馈电路形式就比较复杂,但复杂的反馈电路也总在一定的频率下等效为图8.8.5的形式。

在图8.8.5的基础上增加直流通路和适当的负反馈后,即可得到完整的LC振荡电路。图8.8.6给出一种实用的电容三点式LC振荡电路,其振荡频率近似等于反馈回路的谐振频率:

在振荡频率不是很高的情况下,可以不考虑器件极间电容和分布电容效应,在的范围内选取反馈电压比,以便进一步确定C1和C2的值。并根据电路起振条件AF>1确定A的值。

图8.8.5　三点式LC振荡电路基本形式

图8.8.6　实用的电容三点式LC振荡电路

为了使振荡电路稳定工作,应将晶体管的工作点设置得比较低,以免振荡过程中晶体管进入饱和区而引起输出波形限幅失真。同时,电路中的RE、CE构成自偏电路,随着振荡输出幅度的增加,自生反偏压也增大,使晶体管导通角减小,电路的放大倍数下降,从而达到稳幅的效果。

自偏电路的时间常数RE CE决定了自生反偏压的变化速度,这一速度如果低于振荡幅度变化的速度,则容易导致间歇振荡。为避免间歇振荡,可以取:其中,ω0为振荡角频率,Q为振荡回路Q值。

LC振荡电路频率较高,导致其振幅和频率不稳定的因素很多,有许多是相互关联的,供电电源的波动、元器件参数随环境温湿度的变化、负载的变化等都会影响振荡器工作的稳定性。所以指标要求高的振荡器,应该在多方面采取稳定输出的措施。

①电源和负载

供电电压的变化将导致晶体管的参数如结电容的变化,进而使振荡频率发生改变。性能指标要求高的振荡器,应采取稳压措施确保电源的稳定。负载与回路并联会造成其Q值的下降,降低输出稳定性,可使用射极跟随器降幅,再和回路隔离。

②晶体管

晶体管输入、输出的电抗参数随环境温度、静态工作电流等因素发生变化,这会导致振荡输出的不稳定。为了减小这一影响,应选用fT远高于振荡频率、Cb′c小的晶体管。

③元件

环境温湿度的变化将使回路的电容量和电感量改变,从而使电路的振荡频率发生变化。所以应选择温度系数小的元件,或选择正、负两种温度系数的元件,以取得相互补偿的效果。

④提高回路的Q值。

在电路安装时注意谐振回路与晶体管之间的接线应紧凑可靠,电路远离发热元件,避免机械振动。

3.正弦波振荡器的指标

(1)幅度稳定度S

频率稳定度是指在规定的条件下(例如在一定的范围内改变频率),振荡器输出幅度的相对变化量,其表达式为:

其中,U0为输出电压的标称值,ΔU为实际输出电压与标称值电压之差。

(2)频率稳定度

频率稳定度指在规定的条件下(例如,在一定的范围内改变温度、电压等),振荡器输出频率的绝对或相对变化量。

绝对频率稳定度Δf是实际振荡频率f和额定振荡频率f0的差,表达式为:

相对频率稳定度的定义为: