如何读取和处理测量数据？

1.有效数字与测量数据的读取

在对测量数据进行读取记录以及利用测量数据进行计算的过程中,涉及如何用合理的近似数恰当表达测量结果的问题,即有效数字的问题。有效数字是从数据的左边第一个不为零的数字算起,直到右边最后一位数字为止的所有各位数字,这些数字的个数即是有效数字的位数。例如,0.100 V、330 kΩ、1.05 m A都是三位有效数字。

当只需要N位有效数字时,对第N+1位及其后面的各位数字就要根据舍入规则进行处理,而通常所说的“四舍五入”规则有一定的不合理性,因为“5”是1～9的中间数字,只入不舍显然不合理,应该有舍有入。现在普遍采用的舍入规则是“四舍六入”,具体规则是:

(1)第N+1位为小于5的数时,舍掉第N+1位及其后面的所有数字;若第N+1位为大于5的数时,舍掉第N+1位及其后面的所有数字的同时第N位加1。

(2)当第N+1位恰为“5”时,若“5”之后有非零数字,则在舍5的同时第N位加1;若“5”之后无数字或为0时,则由“5”之前的数的奇偶性来决定舍入,如果“5”之前为奇数则舍“5”且第N位加1,如果“5”之前为偶数则舍“5”,第N位不变。

在测量过程中仪表的量程不同时,所能读出的量值的有效数字位数不同。例如,用三位半的数字电压表测量1.782 V的电压时,如果选用“2V”量程,则电压表的示数为“1.782”;而选用“20V”量程,则电压表的示数为“01.78”;选用“200V”量程,则电压表的示数为“001.7”。由此可见,量程选择过大会丢失有效数字。用数字电压表进行实际测量时一般选择比被测值大但比较接近的量程,使表的示数有尽量多的有效数字,读取数据时可根据具体情况和要求决定保留几位有效数字。

在读取测量数据时,其有效数字位数的保留方法有两种情况:

(1)和误差保持一致,误差不超过有效数字末位单位数字的一半

例如,一只满度为10 V、准确度为0.5级的电压表,测量时的最大绝对误差为

10 V×(±0.5%)=±0.05 V

如果指示值为5.33 V,则实际值范围为5.28～5.38 V,根据误差不超过有效数字末位单位数字的一半的原则,可以记录为5.3 V。但人们习惯上使数据的末位与绝对误差对齐,因此一般还是记录为5.33 V。

(2)直接测量值的有效数字取决于读数时能读到哪一位

例如,量程为50 V的指针式电压表,它的最小刻度是1 V,因读数只能读到小数点后第1位,如30.3 V时,有效数字是三位。若测量时指针正好位于12 V刻度上,数据应记为12.0 V,仍然是三位有效数字(不能记为12 V)。所记录的有效数字中,必须有一位而且只能是最后一位是在一个最小刻度范围内估计读出的,而其余的几位数是从刻度上准确读出的。

由此可知,在记录直接测量值时,所记录的数字应该是有效数字,其中应保留且只能保留一位是估计读出的数字。

2.直接测量数据的处理

(1)单位变换时数据的有效位数不能改变

例如,被测电压记为1 000 m V时,是4位有效数字,表示精确到m V级,进行单位变换时不能写成1 V,因为1 V的写法只有一位有效数字,并且只能表示精确到V级。所以,1 000 m V应该写为1.000 V,不改变有效数字位数,也不改变精确度。

(2)用“10”的方幂来表示数据时,符号“×”前面的数字都是有效数字

例如,3.50×102 V、0.521×104 m W都是三位有效数字。

(3)有效数字的运算

当需要对多个测量结果进行运算时,有效数字的保留原则上取决于误差最大即小数点后有效数字位数最少的那一项。

①加、减运算

先将各数据小数点后的位数处理成与小数点后有效数字位数最少的数据相同后再进行计算。要尽量避免两个相近数的相减,以免对计算结果产生很大的影响,非减不可时,应多取几位有效数字。

②乘、除运算(www.xing528.com)

先将各数据处理成与有效数字位数最少的数据相同或多一位后再进行计算,运算结果的有效数字位数也应处理成与有效数字位数最少的数据相同。注意:在乘、除运算中,有效数字的取舍与小数点无关。

③乘方与开方运算

运算结果应比原数据多保留一位有效数字。

④对数运算

取对数前后的有效数字位数应相等。

3.图解法分析数据

在处理测量结果时,有时需要将被测量随某个或某几个因素的变化规律用曲线表示出来。用曲线表示形象直观,便于分析。要做出一条符合客观规律,反映真实情况的曲线应注意以下几点:

(1)合理选用坐标系

最常用的是直角坐标系,也有用极坐标或其他坐标系的。

(2)合理选择坐标分度

选择适当的坐标分度,确保所绘曲线既能完整呈现整个变化规律,又能清晰展现规律的细节特点。

(3)合理选择测量点

自变量取值的最大值和最小值两个端点、因变量变化的最大值和最小值点都应有准确的测量数据。此外,在曲线变化剧烈的部分要多取几个测试点,以便客观体现曲线的细节;在曲线变化平坦的部分可适当少取测试点。

(4)准确标记测试点

在同一坐标系中作不同曲线时应用不同的符号进行标记,以免相互混淆。

(5)将各测试点用线连起来并修匀曲线

由于测量过程中各种误差的影响,将各测试点连起来所得到的曲线通常都是不光滑的,需要进行修匀以减小误差的影响。修匀曲线通常可以采用以下两种方法:

①直觉法

在精度要求不高或测量点离散程度不大时,用曲线板、直尺凭感觉修匀曲线,作图时不必要求曲线通过每一个测试点,而是从总体上看,曲线尽可能靠近各数据点,且曲线两边的数据点个数基本相等。即各数据点均匀地、随机地分布在曲线的两侧,并且曲线是光滑的。

②分组平均法

把横坐标分成若干组,每组2～4个点,分别求出各组数据的几何重心的坐标,再把这些几何重心连成光滑的曲线,如图4.4.1所示。这种方法由于进行了数据平均,各几何重心的离散程度明显减小,从而使作图更方便和准确。分组的数目应视具体情况而定,分得太细时平均效果不明显,分得太粗则可能因平均点少而增加作图困难,还可能掩盖函数原来的基本特性。因此曲线斜率变化较大或变化规律较重要的地方可分得细一些,曲线较平坦的地方可分得粗一些。

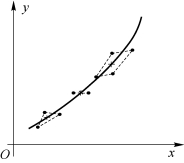
图4.4.1　分组平均法修匀曲线